利用有限简单连分数的最佳逼近原理破译公钥密码RSA及其实现

邓从政

(凯里学院理学院，贵州凯里 556000)

0 引言

一般地，RSA密码体制是利用Zn［1，2］的计算，设n=pq，其中，p，q为素数，ab=1(mod＞ (n)).对此，定义如下的加密函数，ek(x)=xbmodn，和解密函数，dk(y)=yamodn，其中，x，y∈Zn.这样n，b组成了公钥，p，q，a组成了私钥，x是要加密的明文，y =ek(x)是密文，b是加密指数，a是解密指数.假如知道了解密密钥a，那么可以按照以下流程来破译出被加密的明文x.

由于，

有，

假定，x∈Z*N，则有，

式(3)正是我们所期望的解密出来的明文［1］.

从以上的解密流程可以看出，攻击RSA密码体制就是攻击者能够拿到私钥，也就是能够计算出它的解密指数a.如果能做到这一点，那么就可以有效地破解对方发来的密文.事实上，目前有很多种计算私钥a的方法［3，4］，在此基础上，本文介绍一种利用有限简单连分数最佳有理逼近原理计算解密指数的方法来实现对RSA密码体制的有效攻击.

1 有限简单连分数最佳有理逼近原理

事实上，任何一个有理数都可以写成一个有限连分数的形式，

式中，a，b，q1，q2，q3，…，qm，都是非负整数.把［q1，q2，…，qk］，1≤k≤m，称为a/b的第k个渐近分数或者收敛子，容易看出，a/b=［q1，q2，…，qk］，称［q1，q2，…，qk］为连分数a/b的展式.若记，Ek为［q1，q2，…，qk］的第k个收敛子，则每一个Ek可以写成有理数ck/dk的形式，而其中的ck和dk满足如下的递推关系［2］，

且，c0=1，d0=0.

通常，一个有理数的连分数展式有很多有用的性质，基于本研究的目的，最重要的是如下有理数的最佳逼近原理，限于篇幅，这里不作证明.

2 利用逼近原理对RSA密码体制进行有效低解密指数的攻击与实现

假定 n = pq，p和 q为素数，ab≡1(mod＞ (n))，3a＜n1/4，且q＜p＜2q.也就是说，如果n的二进制表示长为x比特，那么当a的二进制表示的位数小于x/4-1比特，且p和q相距很近时就可以进行有效攻击.在此条件下，解密指数a的计算方法如下:

由于，ab≡1(mod＞ (n))，可知存在一个整数t使得，

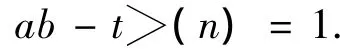
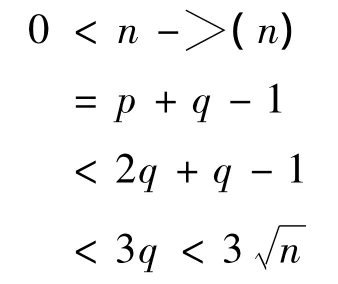
从而，

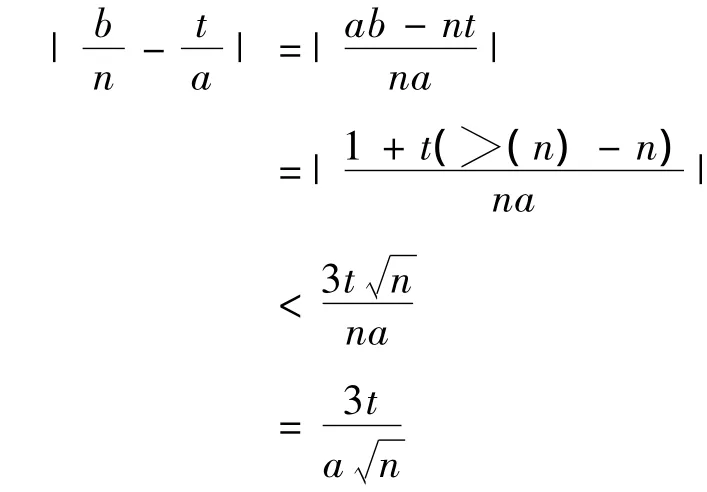
由于，t＜a，有，3t＜3a＜n1/4，因此，

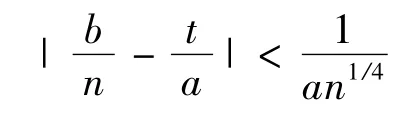
由于，3a＜n1/4，可得，

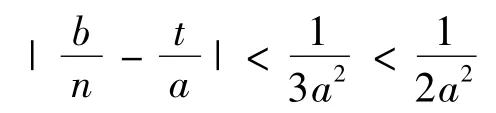
根据有理数的最佳逼近原理，分数t/a是分数b/n的一个最佳渐近分数.n和b是公钥，很容易计算出它的收敛子来.

通过计算，

并解如下方程，

则可以完全分解模n了.

下面给出依据上述逼近原理计算最佳渐近分数的一种算法和一个具体实例.

2.1 威勒算法

威勒算法(Wiener Algorithm)［3］的具体步骤如下:

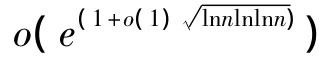
2.2 应用实例

例 设n=160 523 347，b=60 728 973，计算其解密指数a，并且将n分解.

解 ①将b/n展开为连分数，

②验证渐近分数EK.发现，E1、E2、E3、E4、E5不是最佳渐近分数，不能产生n的分解和计算出解密指数a.

④解方程，

得到，x1=12 347，x2=13 001

⑤据此可以把n成功的地分解为，

故所求的解密指数a为，

3 结 论

事实上，攻击RSA密码体制最常用的一种方式就是攻击者试图分解模数n，获得密钥p和q，如果这一点得以实现，那么就可以很简单地计算出，＞(n) =(p-1)(q-1)，然后从b精确地计算出解密指数a，从而破解密文.从本文的分析可以看出，当RSA密码体制所选模数n满足一定的条件时，可以利用连分数的最佳有理逼近原理很快地将模数完全分解并计算出它的解密指数，本文方法不失为攻击RSA密码体制的一种有效方法.因此，一个RSA密码体制要成为安全的，必须要求n=pq充分大，并使之超出现有的分解因子算法的能力，进而使得分解它在计算上是不可行的.

［1］Stinson D R.密码学原理与实践［M］.冯登国译.北京:电子工业出版社，2003.

［2］潘承洞，潘承彪.初等数论［M］.北京:北京大学出版社，2003.

［3］Rivest R L.Shamir A，Adleman L.A Method for Obtaining Digital Signatures and Public Key Cryptosystems［J］.Communications of the ACM，1978，21(2):120-126.

［4］Rosen K H.Elementary Number Theory and Its Applications［M］.New Jersey:Addison-Wesley Publishing Company，1999.