断裂岩石粗糙性与岩体抗剪强度和机理的实验研究

曹秋菊，王金安

(北京科技大学土木与环境工程学院，北京 100083)

自然岩体和工程岩体中普遍存在断裂结构，断裂面是控制岩体长期力学行为[1-2]的主要因素。岩石断裂面[3-6]并非是绝对几何光滑的，而是具有一定粗糙性的[7]。岩体断裂面粗糙性不同，其长期力学行为也会随之变化。

岩石断裂面的粗糙性，可以用“粗糙度”(waviness)和“起伏度”(asperity)两个指标来表征[8]。粗糙度是在较小尺度上表征断裂面的光滑程度，起伏度是在较大尺度上描述断裂面的平整程度。前人对粗糙度的研究较多，用于估算粗糙度的理论方法有许多种，最早的是Barton于1977年提出的节理表面粗糙度系数[9]，而目前最具有代表性的是分形维数计算方法，包括三角形棱柱表面积法、投影覆盖法、立方体覆盖法等[10-14]。对粗糙面起伏度的定量描述还不多见，本文提出了起伏度的一种定量计算方法。并且通过对断裂岩石加载过程中粗糙性演化，揭示构成其长期抗剪强度的机制，本文通过对两类不同破坏方式的断裂岩石进行压剪蠕变实验，并对加载前、加载中和加载后的岩石断裂面进行激光扫描，测试并计算不同阶段断裂岩石双翼表面的粗糙性变化，揭示构成其长期抗剪强度的机理。

1 实验方案

岩样取自山西某矿山的砂岩。其基本物理和力学参数如表1所示。砂岩尺寸为50mm×50mm×50mm，分别由纯剪破坏方式和巴西劈裂拉破坏方式得到两类断裂岩石，如图1所示。

实验具体方法如下：

1)对断裂岩石的两翼进行第一次激光扫描。

2)将扫描过的试件在剪切流变试验机上进行剪切蠕变实验，施加恒定的轴向荷载和分级施加的剪切荷载，如图2所示。试件S1、S2、S3和试件B1、B2、B3施加的轴向荷载，分别为5 MPa、10 MPa和15 MPa。

3)剪切荷载加到估算的抗剪强度值的一半之后卸载，然后打开岩石，对其两翼进行第二次激光扫描。

4)继续对断裂岩石进行剪切蠕变实验，直至试件突然发生较明显的剪切位移。卸载后，对断裂岩石的两翼进行第三次激光扫描。

表1 砂岩物理力学参数表

图1 纯剪破坏和拉破坏的岩石试样

图2 剪切蠕变实验加载方法

2 岩石断裂面粗糙性的计算和演化

在以往的研究中，通常用“粗糙度”这一概念来描述岩石断裂面的凹凸状态。根据摩擦学的原理，岩石断裂表面都是由两种不同的粗糙(或起伏)[8]构成：一种是宏观粗糙度(或宏观起伏度)，它是断裂面上较大的起伏不平，称为“起伏度”；一种是微观粗糙度(或微观起伏度)，它是其起伏面上较小的凹凸不平，称为“粗糙度”。起伏度是在较大尺度上描述断裂面的平整程度，粗糙度是在较小尺度上表征断裂面的光滑程度。起伏度和粗糙度示意图如图3所示。

图3 起伏度和粗糙度示意图

用激光扫描仪对不同加载阶段的断裂岩石两翼进行扫描，将扫描所得数据文件导入Surfer，生成岩石断裂表面凹凸特征图。试件扫描区域为45mm×45mm×45mm，扫描间隔为0.18mm。S1 A面和B2 B面加载前断裂表面凹凸特征如图4所示。图4中所取数据点的间隔为0.36mm。由图4可以看出，纯剪破坏试件S1较巴西劈裂破坏试件B2起伏大，而且B2试件表面则更粗糙些。

注：箭头表示剪力加载方向。

2.1 起伏度分维的计算

过去的研究中，对粗糙度的计算方法已经有很多种，但是对起伏度的定量描述却很少见。投影覆盖法[11]和立方体覆盖法[13]是最有代表性的计算粗糙度的方法。由于岩石断裂表面并不是严格的自相似分形，在计算粗糙度时，这两种方法都是取测量尺度较小时的分形维数计算结果，而并未对码尺较大时的分维计算结果加以分析。因为粗糙度本身描述的就是断裂面上较小的凹凸不平，所以这种取较小码尺计算粗糙度的分形维数的方法是非常合理的。而起伏度描述的是断裂面上的较大的起伏，那么我们可以用码尺较大时测得的断裂岩石凹凸特征的数据来计算岩石断裂面的起伏度，然后确定起伏度分维值与观察到的试件的起伏特征是否一致。

下面用投影覆盖法计算岩石断裂面粗糙度和起伏度的分维值，并确定两者测量码尺的取值范围。由分形理论可知，粗糙表面在二维欧式空间的测度一般可以表示为:

A(δ)=A0δ2-D

(1)

式中：A(δ)为测量尺度为δ时，用投影覆盖法计算出的粗糙表面的面积，mm；A0为按二维计算的岩石断裂面的面积，mm。

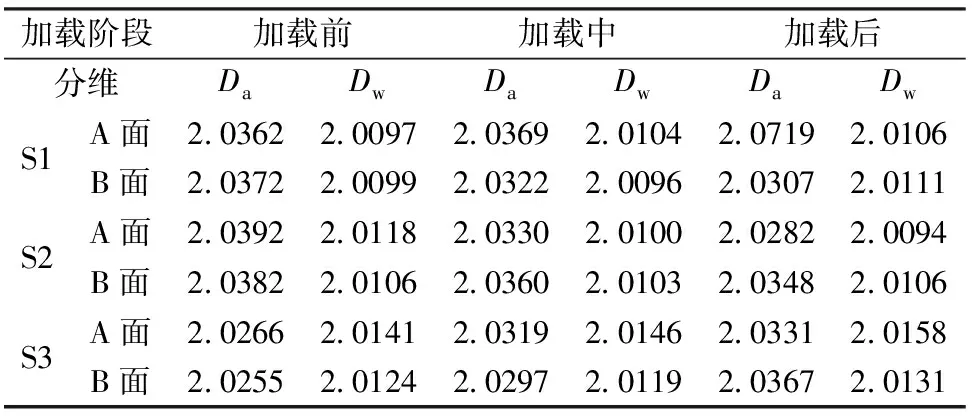
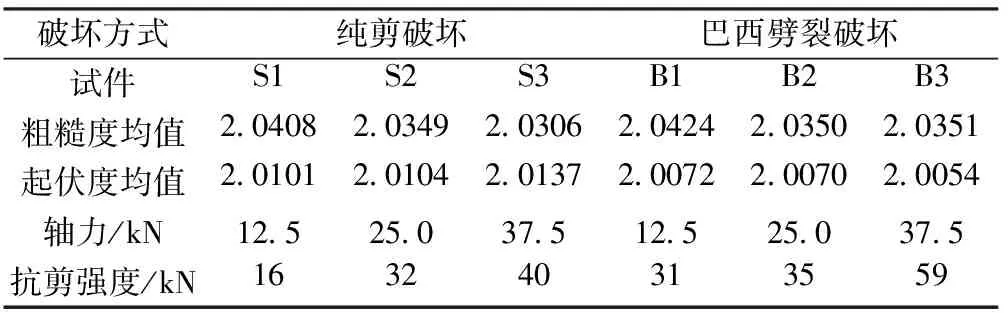
本实验取断裂面上长度和宽度均为45mm的区域，A0=2025mm2；δ为测量尺度，本实验中0.18mm<δ<45mm；D为粗糙表面的真实分形维数，2

由式(1)可以得出：

(k=D-2,且k∈(0,1))

(2)

则D=k+2

由于岩石断裂表面并不是严格的自相似分形，其分形维数值根据码尺的大小分为两段，如图5所示。当码尺0.18mm≤δ≤1.8mm时，线性拟合较好，计算出的分形维数为粗糙度分维，表征起伏面上较小的凹凸不平，用Da表示。若δ的最大值取大于1.8mm的值，数据点线性较差，已经不适用于计算粗糙度分维值。当码尺1.8mm≤δ≤45mm时，线性拟合也较好，计算出的分形维数取为起伏度分维，用以表征断裂面上较大的起伏不平，用Dw表示。图5中，下段直线表示断裂面的起伏度Dw，上段直线表示断裂面的粗糙度Da，这两个参数共同表征断裂面的凹凸特征。需要说明的是，起伏度码尺范围的选取受试件尺寸和测量精度的影响。

图5 试件S1 A面和B2 B面不同加载阶段断裂面的粗糙度和起伏度

纯剪破坏和巴西劈裂破坏方式岩石断裂面的分形维数计算结果如表2和表3所示。由两表可以看出，纯剪破坏岩石断裂面起伏度的分维值为2.0094～2.0158，巴西劈裂破坏岩石断裂面起伏度的分维值为2.0048～2.0079。前者严格大于后者，即纯剪破坏断面的起伏度大于巴西劈裂破坏的断面，与观察到的断裂面的起伏状态一致，即验证了这种计算起伏度的方法是合理的。

表2 纯剪破坏方式岩石断裂面粗糙度和起伏度的分维

表3 巴西劈裂破坏方式岩石断裂面粗糙度和起伏度的分维

下面对起伏度和粗糙度进行分析和比较：

1)分析粗糙度和起伏度的数值。由表2和表3可以看出，无论哪种破坏方式，粗糙度都明显大于起伏度。这是因为粗糙度描述的是较小的凹凸不平，随着码尺变大，很多凹凸体的信息都不参与计算，所以计算出的断裂面面积下降很快，即粗糙度的分维较大。因此，粗糙度越大，岩石断裂面越粗糙。相反，起伏度描述的是断裂面上较大的起伏，随着码尺的增大，断裂面面积也相应变小，但没有计算粗糙度时那么敏感，所以起伏度的分维值较小。

2)比较两类破坏方式的粗糙度和起伏度。由表2和表3的数据可以看出，两类破坏方式的岩石断裂面，粗糙度相差不大，巴西破坏方式岩石断裂面粗糙度略大；而起伏度则是，纯剪破坏方式明显大于巴西劈裂破坏方式。这与观察到的情况是统一的，所以起伏度和粗糙度两者结合能很好的表示断裂岩石表面的凹凸特征。

2.2 加载过程中粗糙度和起伏度的演化特征

由表2和表3的数据可以看出，岩石断裂面的起伏度和粗糙度并不是随着荷载的增加或剪位移的增大而降低。加载过程中，断裂面粗糙度的分维有的变大有的变小，即岩石断裂面出现“粗糙化”或“光滑化”的现象。这是因为加载过程中，随着断裂岩石剪位移的变化，粗糙面接触区域上受剪部分的岩石颗粒有的发生移动，移至粗糙面上相对凹下的区域时，有使之有填平的趋势，分维变小即光滑化；移至粗糙面上相对凸出的区域时，有使之有更粗糙的趋势，分维变大即粗糙化。

然而与粗糙度相比，岩石断裂面的起伏度在加载过程中变化很小。说明压剪荷载对于两接触面上的起伏度影响较小，而对粗糙度的改变相对较大。同时，也因为粗糙度对于断裂表面小的凹凸体变化较敏感，所以其分维值变化相对较大。

3 粗糙度和起伏度对抗剪强度的影响

由表4可见，岩石断裂面的粗糙度，巴西劈裂破坏方式略大于纯剪破坏方式；而断裂面的起伏度，纯剪破坏方式明显且严格大于巴西劈裂破坏方式；纯剪破坏的抗剪强度均大于巴西劈裂破坏。因此，由实验可以得出，断裂面的粗糙度是影响岩石抗剪强度的最主要因素，而起伏度对抗剪强度的影响相对较弱，但其作用也不可忽视。

由于粗糙度描述的断裂面上较小尺度的凹凸不平，断裂岩石需剪断小的凹凸体后才能继续前行；而起伏度描述的是较大尺度的起伏不平，断裂岩石克服两接触面之间的摩擦力后，在剪力作用下就可继续前行。实际上在剪切过程中，粗糙度和起伏度的影响交织在一起，共同影响岩石的抗剪强度，即断裂面的抗剪断能力和抗摩擦能力两者决定了断裂岩石的抗剪强度。

由图1可见，由纯剪破坏方式得到的断裂岩石表面起伏度较大，看起来大的凹凸不平较明显；由巴西劈裂破坏方式得到的断裂岩石表面看起来较平坦，但仔细观察可发现平坦面上较小的凹凸体分布较密集。纯剪破坏岩石断裂面起伏度相对较大，在剪切蠕变过程中，主要是克服凹凸体上的摩擦力才能使两断裂面发生相对移动，但遇到小的凹凸体时，要先将之剪断才能继续克服摩擦力前行。而巴西劈裂破坏断裂面起伏不大，但小的粗糙体相对较多，断裂在剪切蠕变过程中，主要是剪断阻碍其向前移动的密集的粗糙体，在这过程中伴随着克服断裂面上大的起伏在其移动过程中而产生的摩擦力。由实验和分析得出，轴向力相同时，粗糙度大的试件抗剪强度较大，而起伏度起次要作用。

表4 断裂岩石粗糙度、起伏度及抗剪强度对照表

注：粗糙度平均值和起伏度平均值指的是每个试件A、B两面3次扫描的所得的6个分维值的均值。

4 结论与讨论

对由纯剪破坏和巴西劈裂破坏两类方式得到的断裂岩石进行了剪切蠕变实验，同时对加载过程中断裂岩石的两翼进行激光扫描。计算出断裂岩石两翼的粗糙度，并对断裂面的起伏度进行了定量描述。计算得到的起伏度分维值，能够很好地表征断裂面的起伏特征。

实验研究表明，构成断裂岩石长期抗剪强度的机制极其复杂，主要有两个：① 细观凹凸体的抗剪断能力，此因素为粗糙度范畴；② 宏观凹凸体的抗摩擦能力，此因素为起伏度范畴。断裂岩石剪切蠕变过程中剪位移的增加，是通过克服大的凹凸体上的摩擦力和剪断小的粗糙体来实现的，这两种因素同时作用在岩体上。

从上面的分析可以得出，巴西劈裂破坏主要以第一种破坏机制为主，纯剪破坏方式主要以第二种破坏机制为主。实际上，在加载过程中，这两种机制都是交织在一起共同作用于受载岩体上，并随时间或剪位移的增加而相互转换的。

[1] 孙钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报，2007，26(6)：1081-1106.

[2] 张尧，熊良宵.岩石流变力学的研究现状及其发展方向[J].地质力学学报，2008，14(3)：274-285.

[3] 夏才初.岩石结构面的表面形态特征研究[J].工程地质学报，1996，4(3)：71-78.

[4] 贺建明，吴刚.岩体异性结构面的抗剪强度准则[J].重庆大学学报：自然科学版，1994，17 (2)：105-110.

[5] 夏才初，王伟，曹诗定.节理在不同接触状态下的渗流特性[J].岩石力学与工程学报，2010，29(7)：1297-1306.

[6] 何满潮，胡江春，王红芳.岩石表面形态的各向异性及其摩擦特性研究[J].采矿与安全工程学报，2006，23(2)：151-154.

[7] 吴承伟.粗糙表面接触研究进展[J].力学进展，1991，21(1)：96-108.

[8] 陶振宇，唐方福，张黎明，等.节理与断层岩石力学[M].武汉：中国地质大学出版社，1992.

[9] N.Barton，V.Choubey.The shear strength of rock joints in theory and practice [J].Rock Mechanics Felsmechanik Mécanique des Roches，1977，10(2)：1-54.

[10] Clark K C.Computation of the fractal dimension of topographic surfaces using the triangular prism surface area method [J].Computers and Geosciences，1986，12(5)：713-722.

[11] 王金安，谢和平，田晓燕，Kwasniewsk M.A.一种新的断裂表面分形测量方法[J].北京科技大学学报，1999，21(1)：6-9.

[12] Xie H，Wang J A，Stein E.Direct fractal measurement and multifractal properties of fracture surface [J].Physics Letters A，1998，A242：41-50.

[13] 周宏伟，谢和平，Kwasniewsk M.A.粗糙表面分维计算的立方体覆盖法[J].摩擦学学报， 2000，20(6)：455-459.

[14] 张亚衡，周宏伟，谢和平.粗糙表面分形维数估算的改进立方体覆盖法[J].岩石力学与工程学报，2005，24(17)：3192-3196.