后处理工艺Purex流程计算机模拟研究现状及展望

陈延鑫，何 辉，唐洪彬，张春龙，于 婷

中国原子能科学研究院 放射化学研究所，北京 102413

Purex流程是复杂的多级逆流萃取流程，该流程的设计和优化往往需要耗费大量的人力物力，得到的结果却很有限。利用Purex流程中相应组分的分配比、萃取设备的水力学参数等基础数据开展计算机模拟研究，能够在较宽的范围内开展流程的分析和优化工作，找出最佳的工艺条件，具有极其重要的实用价值。

计算机模拟方法的历史可以追溯到20世纪30年代的图表计算方法，当时的Varterressian和Fenske[1]利用该方法计算了符合萃取、洗涤和反萃设计要求所需要的萃取分配系数、两相相对流速和反应器级数等。但这种计算方法只适合于单一溶质或者溶质之间没有相互作用的体系，只是计算机模拟的雏形。

20世纪50年代后期，以计算机技术为基础的图表计算方法继续发展，随后被用于核工业回收和浓缩U、Pu的TBP-煤油液-液萃取流程以及工厂的相关工艺设计。尽管这种方法是图表性质的，并不能解决过程中涉及的动力学问题或对时间有依赖关系的相关问题，但由于其对很多问题能快速给出合适的答案，所以早期采用Purex流程的很多后处理厂的设计是在这种图表计算方法的基础上完成的[2]。

20世纪70年代以来，随着计算机技术的迅猛发展和计算机的普及，大量的计算机模拟程序被开发出来，主要有SIMTEX[3]、SOLVEX[4]、SEPHIS(MOD1—MOD4)[5-7]、VISCO[8]、PULCO[9]、EXTRA·M[10]、CUSEP[11]和PARC[12]。其中SOLVEX、SEPHIS(MOD1—MOD4)、EXTRA·M等程序用来模拟混合澄清槽中各组分的萃取行为，PULCO和CUSEP程序用来模拟脉冲萃取柱，PARC可以模拟混合澄清槽和脉冲萃取柱，VISCO程序则对混合澄清槽、脉冲萃取柱和离心萃取器都能进行模拟。但是由于这些程序的核燃料后处理应用背景，其相关报道不详细。

1 Purex流程计算机模拟体系概述

在核燃料后处理Purex流程中，同时存在硝酸、铀、钚、还原剂和微量组分镎、裂片元素等多种组分，含有溶质的硝酸水相通过与TBP-煤油有机相逆流接触，发生传质达到萃取平衡。对于等温等压条件下的某一萃取体系来说，该体系任何组分的分配比是一定的，与设备及工况等因素无关，组分的分配比只会随着萃取体系中的硝酸浓度、其他组分浓度以及所使用的萃取剂浓度等的变化而变化，而在实际工业生产中，由于所使用的设备和工况的差异，组分在两相间的分配还由传质速率和化学平衡来确定，操作温度、各组分浓度和两相的接触情况均影响传质速率和化学平衡，进而影响到流程中各组分在两相中的分配情况。因此，Purex流程计算机模拟研究需在大量研究各组分化学行为、分配比数据、动力学数据等基础上，建立各组分的分配比模型函数，同时结合Purex流程中所使用的萃取设备开展水力学研究，建立不同类型萃取设备的数学模型，从而分别开展Purex流程的计算机模拟研究，最终根据不同后处理厂的设备选用情况进行全流程计算机模拟研究。Purex流程计算机模拟体系具体示于图1。

图1 Purex流程计算机模拟总体设计

2 分配比模型

分配比是指萃取达到平衡后，被萃物在有机相的总浓度与水相中的总浓度之比值，也称分配系数，以符号D表示。物质的分配比大小与它本身的性质、萃取剂性质以及萃取体系中的其他条件有关。在Purex流程中，通过控制不同的工艺条件，造成分配比的变化和差别，以实现萃取、分离和反萃取的目的。

由于分配比的复杂可变性，从20世纪70年代开始，国外的研究者[13-19]就对不同萃取体系下的HNO3、U、Pu等组分的分配比进行过系统研究，并试图在大量分配比数据的基础上，拟合出Purex流程中相关组分的分配比模型，拟合的方法主要有两种：一种是在理论分析的基础上通过数据拟合得到分配比模型，函数公式中的参数具有一定的物理意义，其中最有代表性的是美国的Richardson模型[19]和俄罗斯Bochvar无机材料研究所(AUSRIIM)的研究者Rozen拟合的模型[20](以下简称Rozen模型)；另一种是完全通过数据拟合得到的分配比模型(以下简称拟合模型)[10]，函数公式中的参数完全没有物理意义。

2.1 半理论模型

Richardson分配比模型涵盖了Purex流程中HNO3、U(Ⅵ)、Pu(Ⅲ)、Pu(Ⅳ)四种组分。通过这些金属离子Mm+在TBP-HNO3中的热力学萃取平衡常数计算公式，建立起分配比D与表观平衡常数、自由TBP浓度、总硝酸根浓度之间的关系，模型公式为:

DM=co(M(NO3)m·nTBP)/ca(Mm+)=

(1)

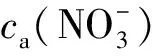
4c(Pu4+)+3c(Pu3+)+Sa

(2)

式中Sa代表其他硝酸盐及其他不被有机相萃取的离子总浓度。

对于不同温度、不同TBP浓度下的分配比差异主要通过调节表观平衡常数来实现，具体的方法可以参考文献[21]。从而，各组分的分配比可表示为：

(3)

(4)

(5)

(6)

式中的自由TBP浓度cf(TBP)可通过对TBP物料衡算得到，具体方法参照文献[14]。

针对Richardson分配比模型的缺点，俄罗斯Bochvar无机材料研究所(AUSRIIM)的Rozen[20]提出用离子强度来代替总硝酸离子浓度进行拟合的方法。目前采用这种方法对U(Ⅵ)、Pu(Ⅵ)、Np(Ⅵ)、U(Ⅳ)和Pu(Ⅲ)五种组分进行了修正，得到的修正模型为：

3.29×10-3I3+1.18×10-4I4

(7)

其中I为实际有效离子强度：

I=c(H)+3c(U(Ⅵ))+

c(Pu(Ⅳ))+3c(Pu(Ⅵ))

(8)

同时，相对于Np(Ⅵ)与Pu(Ⅵ)的活度系数有：

γNp(Ⅵ)=γU(Ⅵ)(1-9.8×10-3I)

(9)

γPu(Ⅵ)=γU(Ⅵ)(1-1.96×10-3I)

(10)

(11)

对于Np(Ⅳ)，其表观平衡常数则直接与Pu(Ⅳ)的表观平衡常数拟合，同时根据是否存在U(Ⅵ)，分别加以修正，得到的模型为：

(12)

当有U(Ⅵ)共存时：

(13)

同样，对于U(Ⅳ)，拟合后的模型公式为：

(14)

对于Pu(Ⅲ)，由于缺乏活度系数的数据，在拟合时采用Nd(Ⅲ)的数据代替Pu(Ⅲ)进行拟合：

lnγPu(Ⅲ)=-7.53I/(1+2.84I)+

0.391I+0.040 7I2+5.57×10-4I4

(15)

Rozen模型将各组分的活度系数作为新的参数引入了模型，从原理上使模型与实际更趋近了一步，同时拟合了Pu(Ⅲ)和U(Ⅳ)的活度系数或表观萃取常数，从而解决了Richardson模型在模拟计算这两种组分时的偏差较大的问题。但是，不同组分在不同条件下的活度系数毕竟很难测定，有些组分由于价态变化迅速等原因甚至无法测定，或者测定的数据也无很好的重现性，因此，该模型还需进一步的深化和改进。

2.2 拟合模型[10]

鉴于理论推导中有些参数无法测定，日本原子能研究所于20世纪90年代摒弃了复杂的理论推导和分析，完全从大量的分配比数据出发，拟合了HNO3、U(Ⅳ)、U(Ⅵ)、Pu(Ⅲ)、Pu(Ⅳ)、Pu(Ⅴ)、Pu(Ⅵ)、Np(Ⅳ)、Np(Ⅴ)、Np(Ⅵ)、Tc(Ⅶ)、Zr(Ⅳ)的分配比模型公式。针对硝酸和金属离子分别采用两种公式加以拟合如下：

硝酸的分配比拟合公式：

(16)

金属离子分配比拟合公式：

(17)

与Richardson模型和Rozen模型相比，该模型拟合的组分众多，几乎包含Purex流程中的全部组分，该模型在程序EXTRA·M上得到了应用，EXTRA·M的作者通过文献数据及一系列的实验验证了该模型的可靠性，具有极其重要的实用参考价值。但是，该模型拟合的仅仅是30％TBP浓度、25 ℃条件下的数据，无法考察不同TBP浓度、不同温度条件对流程的影响，有一定的缺陷。

2.3 国内情况

国内也开展过类似研究，如李光鸿等[22]对铀、钚以及硝酸的分配比数据做过较为系统的研究，拟合了相应组分的分配比模型，同时对微量钚条件下的分配比数据做了研究，弥补了Richardson模型的部分缺陷；陶成英等[23-24]对U(NO3)4-HNO3-H2O/30％TBP-煤油萃取体系下的U(Ⅳ)分配比进行了系统的测量和研究，拟合了U(Ⅳ)的分配比数学函数，U(Ⅳ)分配比函数的计算误差均值为7.1％；另外，中国科学院上海应用物理研究所的杨金峰等[25]对铀、钍核燃料后处理萃取过程开展了计算机模拟工作，获得了铀、钍的分配比模型，为铀、钍核燃料后处理萃取过程计算机模拟研究奠定了基础。

3 级式萃取设备模拟

级式萃取设备包括混合澄清槽和离心萃取器两种，能够区分出明确的萃取级。由于两相流体在级式萃取设备的各级混合比较充分，此类设备的数学模型在流体状态上均可以采用全混流模型。国内外对于此类设备的模拟也都是采用全混流模型而开展模型函数的建立工作的，区别在于考虑参数的量不同。

美国橡树岭国家实验室于1970—1974年间，先后开发了SEPHIS程序的四个版本用于Purex流程不同工艺段的分析和优化工作。该程序将多级混合澄清槽的一级分为1个混合室和3个澄清段加以建模(图2)。

图2 SEPHIS(MOD1—MOD4)采用的混合澄清槽模型

其中每一级混合室接受来自相邻级的液流(Aj-1和Oj+1)或由萃取器外引入的料液(Afj和Ofj)，流出液从澄清室的第三室流出(APj和OPj)，可以为下一相邻级提供料液(Aj和Oj)或生成产品液(APj和OPj)而离开萃取器，也可以设定内部料液循环模式(Afj和Ofj)。根据以上思想，从设备运行的不平衡阶段作为开始，建立各级萃取器的模型公式如下：

Oj+1yi,j+1+Af,jxf,i,j+Of,jyf,i,j-

(Aj+Ap,j)xi,j-(Oj+Op,j)yi,j

(18)

由于假设萃取器的容积和流体的流量是恒定的，并且认为各级的萃取都能够达到萃取平衡，从而两相间的组分浓度满足：

yi,j=Dixi,j

(19)

通过联立以上两式就可以解得稳态时两相的各组分浓度。该模型仅涵盖Purex流程中的HNO3、U(Ⅵ)、Pu(Ⅲ)、Pu(Ⅳ)四种组分，同时可模拟以U(Ⅳ)、HAN、Fe2+中的其中一种作为还原剂的模拟研究。该程序主要用于模拟以混合澄清槽作为萃取设备的Purex流程的相关工艺工程，虽然也可以用于脉冲萃取柱的模拟，但是模拟结果较差。

EXTRA·M程序是日本核能研究机构东海研究所的燃料循环安全工学部于1989年至1994年开发的[10]，该程序仅以混合澄清槽作为模拟对象，继承了SEPHIS程序的数学模型建立方法，同时对该模型进行了简化，忽略了有机相料液的内循环，仅考虑水相的料液循环，因此简化了模型计算过程。另外，鉴于SEPHIS程序所涵盖的组分数目较少的缺点，该程序添加了Np(Ⅳ、Ⅴ、Ⅵ)、Tc、Zr、Ru等18种组分的分配比模型，大大提高了程序的模拟范围和实用性。该程序分为3个版本，其中EXTRA·M1版本涵盖8个氧化还原反应，EXTRA·M2版本涵盖30个氧化还原反应，EXTRA·M3涵盖18个氧化还原反应。通过考虑氧化还原反应，就可以模拟组分在不同条件下的价态变化对流程的影响情况，使程序模拟与实际情况更加接近，可靠性和准确度都有了较大幅度的提高。

日本原子力基础工学研究部于2008年发布了一个新开发的程序PARC[12]，该程序可实现对混合澄清槽和脉冲萃取柱两种设备的模拟。对于混合澄清槽的模拟仍然继承了SEPHIS程序所采用的模型，不同的是，PARC程序不再将混合澄清槽的澄清室分为3个澄清段建模，而是和实际的混合澄清槽一样，分为1个混合室和1个澄清室分别进行物料衡算，从而建立数学模型，使得模型和实际更加趋近。与EXTRA·M中涵盖的Purex流程组分数相比，PARC共涵盖了29种组分，除了包含HNO3、U(Ⅳ、Ⅵ)、Pu(Ⅲ、Ⅳ)等组分外，还添加了因辐解而产生的DBP、MBP等。PARC程序除了能够实现稳态条件下各级的浓度剖面计算外，由于考察了时间因素，还能够实现混合澄清槽运行状态的动态模拟。在模型参数方面，由于添加了总传质系数和传质面积，使模拟结果与实际值更加接近。

国内从20世纪70年代开始也开展了类似的研究，中国原子能科学研究院的陶成英[26]曾就3B工艺段中羟胺还原钚的工艺流程进行了计算机模拟研究，通过27次的模拟计算，探索研究了5个重要因子对3B槽钚收率和分离系数影响的定量关系，从而节省了大量的人力和时间，为后期的计算机模拟工作奠定了良好的基础。到了21世纪初，中国原子能科学研究院的何辉[27]采用新型还原剂N,N-二甲基羟胺作为还原剂开展了相关的计算机模拟工作，同时采用稳态趋近模型对1A工艺段开展了计算机模拟工作，以典型的1A工艺流程作为输入条件，考察了流量变化对铀钚收率的影响，获得了流量的边界条件，为工艺运行提供了参考。

4 微分式萃取设备模拟

与混合澄清槽不同，两相流体在脉冲萃取柱内传质始终处于不平衡状态，无法划分出明确的萃取级，组分在两相间的传质除了依靠浓度差的传质推动力之外，还与外界能量输入有很大的关系，因此，脉冲萃取柱的数学模型与混合澄清槽有较大的差别。国内外对于脉冲萃取柱的模拟也开展了大量的研究，但是真正能够适用于后处理工艺Purex流程模拟的程序软件并不多见，目前见诸报道的仅有日本的PULCO程序、英国的CUSEP程序、Hass程序、Visco程序和近期的PARC程序，这些程序大部分都没有进行详细报道，仅就其中的部分内容给予了介绍。通过对比相关的文献报道，脉冲萃取柱的计算机模拟研究主要采用的数学模型有2种，分别是20世纪五、六十年代由Danckwerts以及Sleicher分别建立的扩散模型和返混模型。由于返混模型较多的应用于RDC、Scheibel柱，对于有强烈凝聚和再分散的场合较为适用；而扩散模型不但考虑了筛板内的传质和返混特性，而且物理意义又较为明确，所以国内外的大部分研究者都采用扩散模型来描述脉冲萃取柱内流体流动行为和传质行为。

扩散模型(或称轴向扩散柱塞流模型)假定在连续逆流传质过程中，除了相际传质外，每相中都存在从高浓度向低浓度的扩散传递过程，将柱内所有使其偏离柱塞流模型的原因归结为两个轴向扩散系数Ex、Ey，每一相中的扩散都符合Fick定律。该模型假设分散相亦为一“连续相”，这样使模型能够较好的预测连续相的轴向混合，模型示意图示于图3。

图3 扩散模型示意图

图3中表示的是两相逆流接触(假设Y相为分散相)，取其中一个微元作物料衡算，设向下为正方向，柱子截面积为S，留存分数为Φ，柱高为H，微元高为dh，且假设在两相逆流接触过程中，两相流速ux、uy不发生变化。在微元内X相体积为(1-Φ)Sdh，Y相体积为ΦSdh。经过相关的物料衡算以及归一化得到一个方程组。

动态条件下：

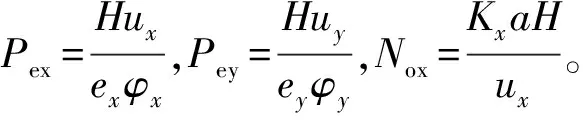
当多组分共存时，该方程组的计算十分复杂，后期的研究者都进行了大量的研究以合理简化该模型方程。Steiner等[28]实验发现，即使分散相的轴向扩散系数发生了显著的变化，沿脉冲萃取柱轴向的浓度变化也非常小，因此趋向于将分散相的轴向扩散系数忽略，该研究也得到了其他一些研究者[29]的认同。

另外，随着水力学研究的深入以及技术手段的增强，液滴的尺寸分布被越来越多的研究者所重视。由Olney[30]首先报道液滴尺寸分布的影响以来，一些研究者[31-34]研究认为，相对于液滴的尺寸分布来说，分散相的轴向扩散系数可以被忽略。因此，最近的一些相关研究都从液滴的角度去考虑分散相的相关行为，将液滴按照不同的尺寸归类，认为每一类液滴有着各自的传质速率，然后通过积分得到模型方程。

我国对于后处理工艺Purex流程体系下的脉冲萃取柱计算机模拟研究尚不充分。尽管清华大学对脉冲萃取柱的操作性能、流体力学等方面开展过较详细的研究[35-43]，对脉冲萃取柱的数学模型和解法等方面也取得了一定的研究成果[31-34]，但是这些研究都停留在单组分硝酸体系下，在应用到核燃料后处理工业中的脉冲萃取柱模拟时还存在一系列需要解决的问题，如多组分共存体系的模型数学解法、后处理体系中各组分的传质系数等。

5 结论与展望

对于后处理工艺Purex流程计算机模拟已经开展了大量的研究工作，在各组分分配比模型、混合澄清槽模拟、脉冲萃取柱模拟等方面都取得了令人瞩目的成就。由于程序的核燃料后处理应用背景，大部分均未完全公开，就目前获得的文献资料可知：

(1)分配比模型研究是计算机模拟研究的基础；目前的分配比模型主要采用半理论模型，其中最具代表性的是Richardson模型，在该模型的基础上，通过拓宽组分数目和引入新的参数等方法，能够使模型的可靠性和准确性进一步提高；

(2)混合澄清槽和离心萃取器都属于级式萃取设备，该类设备的模拟研究主要集中于混合澄清槽；根据混合澄清槽的流体状态，一般选用全混模型来建立数学模型，国内采用稳态趋近算法具有较好的可靠性和准确度；由于离心萃取器的使用较少，目前以离心萃取器开展Purex流程计算机模拟的程序较少；

(3)脉冲萃取柱主要采用扩散模型进行研究，由于模型中涉及大量的水力学参数，因此，除需分配比数据作为基础数据外，还需建立可靠的水力学参数模型，才能保证模拟的可靠性和准确度。

目前，对于Zr、Ru、HNO2等化学形态和萃取行为复杂的组分，适用数据拟合的方式获得分配比模型；对于相对含量较高且化学行为研究充分的组分，适宜采用半经验模型。对于混合澄清槽和脉冲萃取柱计算机模拟，国内现阶段仅能模拟组分价态不变化、不涉及氧化还原反应的计算，因此，需进一步开展涉及氧化还原反应、高浓度钚的模拟研究；同时，还应加强离心萃取器方面的计算机模拟研究工作。

[1]Varterressian K A， Fenske M R.Liquid-Liquid Extraction Performance of a Packed Extraction Column Using Continuous Current Operation[J].Ind Eng Chem,1936,28: 928.

[2]Schulz W W,Navratil J D,Burger L L.Science and Technology of Tributyl Phosphate Vol(Ⅱ): Applications of Tributyl Phosphate in Nuclear Fuel Processing[M].The United States: CRC Press,Inc,1990: 183-184.

[3]Burton W R,Mills A L.Computer Calculation of Flowsheets for Reprocessing Nuclear Fuels[J].Nucl Eng,1963,8: 248.

[4]Scotten W C.SOLVEX-A Computer Program for Simulation of Solvent Extraction Processes: DP-1391[R].Aiken,SC,USA: Du Pont De Nemours (E.I.)and Company,1975.

[5]Richardson G L.Effect of High Solvent Irradiation Exposures on TBP Processing of Spent LMFBR Fuels: HEDL-TME 73-51[R].USA: OAK Ridge National Laboratory,1973.

[6]Mitchell A D.SEPHIS-MOD4: A User′s Manual to a Revised Model of the Purex Solvent Extraction System: ORNL-5471[R].USA: OAK Ridge National Laboratory,1979.

[7]Watson S B,Rainey R H.Modification of the SEPHIS Computer Code for Calculating the Purex Solvent Extraction System: ORNL/TM-5123[R].USA: OAK Ridge National Laboratory,1975.

[8]Petrich G.The Purex Process Computer Model “VISCO” and Its Application[C].Proc Int Solvent Extraction Conf,Dechema,Munich,West Germany,Vol.1,1986: 427.

[9]Gonda K,Matsuda T.Calculation Code PULCO for PUREX Processes in a Pulsed Column: PNCT-841-82-19[R].Japan: Power React and Nucl Fuel Dev Corp,1982.

[10]Tachimoli S.EXTRA·M: A Computing Code System for Analysis of the Purex Process With Mixer Settler for Reprocessing: JAERI-1331[R].Japan: Japan Atomic Energy Research Institute,1993.

[11]Geldard J F,Beyerlein A L.CUSEP—A New Mathematical Model of Pulsed Column Contactors Using the PUREX Process[J].Nucl Tech,1989,85: 172-186.

[12]Tsubata Y,Asaura T,Morita Y.Development of a Computer Code,PARC,for Simulation of Liquid-Liquid Extraction Process in Reprocessing: JAEA-2008-010[R].Japan: Japan Atomic Energy Agency,2008.

[13]Youichi E,Ichiro Y.Distribution Coefficient Correlations for Nitric Acid,U(Ⅵ)and Pu(Ⅳ)in Two-Phase System With Aqueous Nitric Acid and 30％ Tri-n-Buthylphosphate Solutions[J].J Nucl Sci Tech,1997,34(7): 700-707.

[14]Alcock K,Bedford F C,Hardwick W H,et al.Tri-n-Butyl Phosphate as an Extracting Solvent for Inorganic Nitrates: Ⅰ Zirconium Nitrates[J].J Inorg Nucl Chem,1957,4: 100-105.

[15]Scargill D,Alcock K,Fletcher J M,et al.Tri-n-Butyl Phosphate as an Extracting Solvent for Inorganic Nitrates: Ⅱ Yttrium and the Lower Lanthanides Nitrates[J].J Inorg Nucl Chem,1957,4: 304-314.

[16]Best G F,Mckay H A C,Woodgate P R.Tri-n-Butyl Phosphate as an Extracting Solvent for Inorganic Nitrates: Ⅲ The Plutonium Nitrates[J].J Inorg Nucl Chem,1957,4: 315-320.

[17]Hesford E,Mckay H A C,Scargill D.Tri-n-Butyl Phosphate as an Extracting Solvent for Inorganic Nitrates: Ⅳ Thorium Nitrate[J].J Inorg Nucl Chem,1957,4: 321-325.

[18]Uchiyama G,Hotoku S,Fujine S.Distribution of Nitrous Acid Between Tri-n-Butyl Phosphate/N-Dodecane and Nitric Acid[J].Solvent Extr Ion Exch,1998,16(5): 1 177-1 190.

[19]Richardson G L,Swanson J L.Plutonium Partitioning in the Purex Process With Hydrazine-Stabilized Hydroxylamine Nitrate: HEDL-TME 75-31[R].USA: OAK Ridge National Laboratory,1975.

[20]Rozen A M,Andrutskii L G,Vlasov V S.Improved Mathematical Models of Actinide Extraction by 30％ Solutions of the Tri-n-Butylphosphate in Diluents[J].At Energy,1987,62(4): 264-271.

[21]何辉，李高亮，陈辉,等.Purex流程共去污工艺计算机稳态模拟[J].原子能科学技术，2008，42(9): 784-789.

[22]李光鸿，刘秋生，王乃陶.UO2(NO3)2-HNO3-H2O/30％(体积)TBP-240号煤油体系萃取过程的数学模型:Ⅰ.计算铀、酸分配数据的数学模型[J].核化学与放射化学，1979，1(1)：42-56.

[23]陶成英.U(NO3)4-HNO3-H2O/30％TBP-煤油萃取体系平衡分配数据及其数学描述[J].原子能科学技术，1986，20(1)：13-18.

[24]陶成英，费洪澄.U(NO3)4-HNO3-H2O/30％TBP-煤油体系萃取平衡分配数据的测定[J].原子能科学技术，1988，22(2)：185-191.

[25]杨金峰，包伯荣，夏源贤,等.钍铀核燃料后处理萃取过程的数学模拟及工艺流程的计算机优化[J].核化学与放射化学，1992，14(1)：27-43.

[26]陶成英.萃取过程的计算机数学模拟研究:Ⅱ Purex过程3B槽羟胺还原工艺条件的选择[J].原子能科学技术，1983，17(2):174-181.

[27]何辉，胡景炘，张先业,等.N,N-二甲基羟胺对Pu(Ⅳ)的还原反萃和相应的计算机模型[J].核化学与放射化学，2001，23(2):65-71.

[28]Steiner L,Bertschmann H,Hartland S.A Model for Simulation of Hydrodynamics and Mass Transfer in Extraction Columns Filled With Regular Packing[J].Trans IChemE: Part A,1995,73: 542-550.

[29]Morales C E,Perez H A.Modeling and Simulation of a Liquid Extraction Column With Structured Packing[J].Comput Chem Eng,2007,31: 1 694-1 701.

[30]Olney R B.Droplet Characteristics in a Countercurrent Contactor[J].AIChE J,1964,10(6): 827-835.

[31]Tang X J,Luo G S,Li H B,et al.Two-Phase Flow Characteristics in a Coalescence-Dispersion Pulsed-Sieve-Plate Extraction Column[J].Chin J Chem Eng,2004,12: 1-6.

[32]Tang X J,Luo G S,Wang J D.A Dynamic Forward Mixing Model for Evaluating the Mass Transfer Performances of an Extraction Column[J].Chem Eng Sci,2004,59: 4 457-4 466.

[33]Tang X J,Luo G S,Wang J D.An Improved Dynamic Combined Model for Evaluating the Mass Transfer Performances in Extraction Columns[J].Chem Eng Sci,2005,60: 4 409-4 421.

[34]Tang X J,Luo G S,Li H B,et al.A Dynamic Interaction Mass Transfer Model for Simulating the Mass Transfer Process in Extraction Columns[J].Comput Chem Eng,2006,30: 978-988.

[35]张惟博，戴为智，胡熙恩,等.梯形波脉冲筛板萃取柱流体力学性能[J].高等化学工程学报，1993，7(3):207-213.

[36]张惟博，戴为智，胡熙恩.梯形波脉冲筛板萃取柱传质性能[J].高等化学工程学报，1993，7(3)：214-220.

[37]邰德荣，戴为智，胡熙恩,等.梯形脉冲筛板萃取柱性能的研究[J].原子能科学技术，1989，23(3)：26-32.

[38]毕升，景山，吴秋林,等.30％TBP-煤油/HNO3体系在折流板脉冲萃取柱中的水力学性能[J].原子能科学技术，2007，41(7)：410-415.

[39]马荣林，陈靖，徐世平,等.脉冲筛板萃取柱中30％TRPO-煤油/硝酸体系流体力学性能研究[J].原子能科学技术，2000，34(1)：54-58.

[40]钱宇，费维扬，汪家鼎.脉冲筛板萃取柱中传质过程研究[J].化工学报，1988，5：522-529.

[41]朱慎林，张宝清，沈忠耀,等.脉冲筛板萃取柱中两相流体力学的研究[J].化工学报，1982，1：1-13.

[42]毛宗强，公锡泰，马栩泉,等.脉冲筛板柱萃取分离镍钴的半工业实验[J].有色金属，1995，47(1)：44-48.

[43]王悦云，吴秋林.脉冲折流板萃取柱板间距对流体力学性能影响-30％TRPO-煤油/硝酸体系[J].核科学与工程，2003，23(1)：68-72.