一类具变时滞细胞神经网络的全局渐近稳定性

常 青，周立群

（天津师范大学 数学科学学院，天津 300387）

一类具变时滞细胞神经网络的全局渐近稳定性

常 青，周立群

（天津师范大学 数学科学学院，天津 300387）

讨论一类具变时滞细胞神经网络平衡点的唯一性和全局渐近稳定性，利用矩阵不等式，通过构造合适的Lyapunov泛函，得到了具变时滞细胞神经网络全局渐近稳定性的新的充分条件.

细胞神经网络；变时滞；全局渐近稳定性；矩阵不等式；Lyapunov泛函

细胞神经网络模型于1988年由Chua L.O.等首次提出［1－2］，它是一种能实时、高速并行处理信号的大规模非线性模拟电路模型，易于VLSI实现，可描述三阶以上的动力学行为.1990年，Roska T.等提出了时滞细胞神经网络模型［3］.细胞神经网络模型和时滞细胞神经网络模型在图像处理、模式识别、联想记忆等领域有广泛应用.近年来，许多学者对细胞神经网络的动力学行为，尤其是网络的动态性，如网络平衡点的存在性、唯一性以及全局渐近稳定性和全局指数稳定性，进行了深入研究并取得了很多成果［4－12］.文献［12］利用矩阵不等式和Lyapunov泛函研究了激活函数为分段线性函数f（x）＝0.5（｜x＋1｜＋｜x－1｜）的具常时滞细胞神经网络平衡点的唯一性和全局渐近稳定性.在此基础上，本研究扩大激活函数的范围，利用矩阵不等式和构造合适的Lyapunov泛函研究了具变时滞细胞神经网络平衡点的唯一性和全局渐近稳定性，得到了具变时滞细胞神经网络全局渐近稳定性的新的充分条件.

1 预备知识

考虑具变时滞细胞神经网络系统

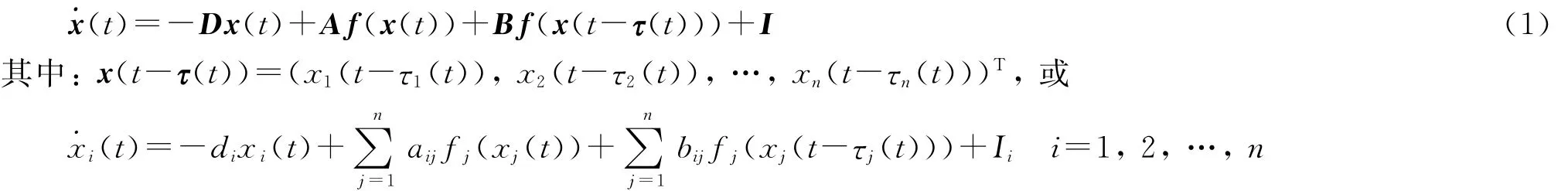
2 主要结果

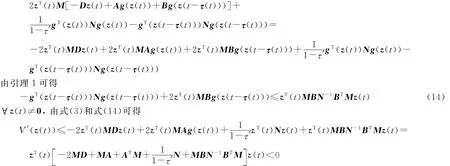
所以原点是系统（2）的全局渐近稳定点.证毕.

注1 若在系统（1）中令D＝I（单位矩阵），x（t－τ（t））＝x（t－τ），则系统（1）就是文献［12］讨论的模型.定理1与定理2中当τ′＝0时就是文献［12］中当β＝1时的结果.

3 算例及仿真

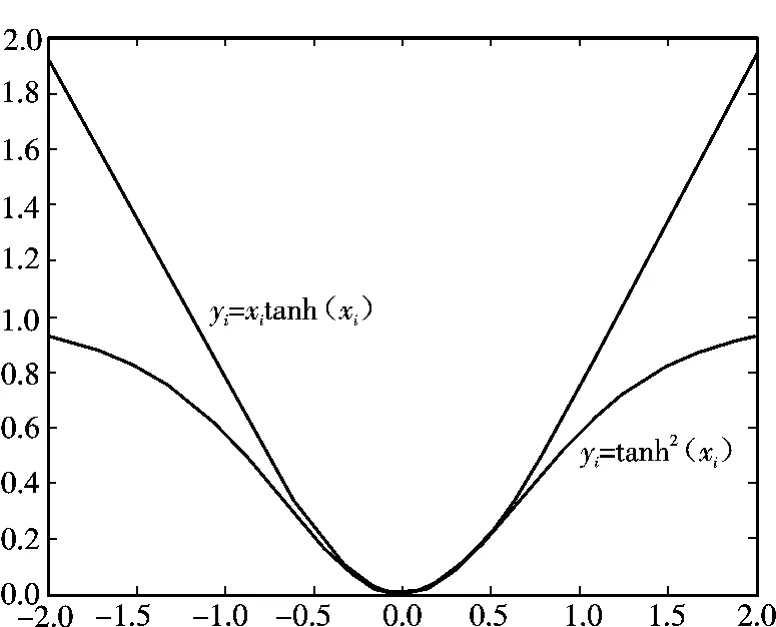
图1 tanh2（xi）≤xitanh（xi）Fig.1 tanh2（xi）≤xitanh（xi）

图2 系统（15）的仿真图Fig.2 Simulation of system （15）

［1］ CHUA L O，YANG L.Cellular neural networks：theory［J］.IEEE Transactions on Circuits and Systems，1988，35：1257－1272.

［2］ CHUA L O，YANG L.Cellular neural networks：applications［J］.IEEE Transactions on Circuits and Systems，1988，35：1273－1290.

［3］ ROSKA T，CHUA L O.Cellular neural networks with nonlinear and delay－type template elements and nonuniform grids［J］.International Journal of Circuit Theory and Applications，1992，20：469－481.

［4］ ZHANG Q，WEI X P，XU J.Delay－dependent exponential stability of cellular neural networks with time－varying delays［J］.Chaos，Solitons and Fractals，2005，23：1363－1369.

［5］ SINGH V.Global asymptotic stability of cellular neural networks with unequal delays：LMI approach［J］.Electronics Letters，2004，40：548－549.

［6］ CAO J D，LI Q.On the exponential stability and periodic solutions of delayed cellular neural networks［J］.Journal of Mathematical Analysis and Applications，2000，252：50－64.

［7］ PENG J G，QIAO H，XU Z B.A new approach to stability of neural networks with time－varying delays［J］.Neural Networks，2002，15：95－103.

［8］ SUN C Y，FENG C B.Exponential periodicity and stability of delayed neural networks［J］.Mathematics and Computers in Simulation，2004，66：469－478.

［9］ HUANG C X，HUANG L H，YUAN Z H.Global stability analysis of a class of delayed cellular neural networks［J］.Mathematics and Computers in Simulation，2005，70：133－148.

［10］ ZHOU L Q，HU G D.Global exponential periodicity and stability of cellular neural networks with variable and distributed delays［J］.Applied Mathematics and Computation，2008，195：402－411.

［11］ SONG X L，PENG J G.Exponential stability of a class of neural networks with discrete time－varying and distributed delays［J］.Chinese Journal of Engineering Mathematics，2010，27：731－740.

［12］ 刘静.对延迟细胞神经网络全局渐近稳定性一个结果的改进［J］.大学数学，2010，26：26－29.

Global asymptotic stability of a class of cellular neural networks with variable delays

CHANGQing，ZHOULi－qun
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

The uniqueness and the global asymptotic stability of the equilibrium point of a class of cellular neural networks with variable delays are studied.In virtue of constructing a linear matrix inequality and a suitable Lyapunov functional，new sufficient conditions are derived for the global asymptotic stability of the cellular neural networks with variable delay.

cellular neural networks；variable delays；global asymptotic stability；linear matrix inequality；Lyapunov functional

O175.13

A

1671－1114（2012）01－0006－04

2011－06－21

国家自然科学基金资助项目（60974144）；天津市高等学校科技发展基金计划资助项目（20100813）；天津师范大学博士基金资助项目（52LX34）

常 青（1988—），女，硕士研究生.

周立群（1972—），女，博士，副教授，主要从事神经网络稳定性、随机微分方程数值方法的稳定性和收敛性方面的研究.

（责任编校 马新光）