神府煤田建设中扰动地面水沙过程模拟研究

黄鹏飞，刘敏，王文龙，3†，罗婷

(1.中国科学院 水利部 水土保持研究所，黄土高原土壤侵蚀与旱地农业国家重点实验室，712100 陕西杨凌;2.杨凌区水务局水利水保站，712100 陕西杨凌;3.西北农林科技大学水土保持研究所，712100 陕西杨凌;4.杭州大地科技有限公司，310000，杭州)

伴随我国生产建设项目的日益增多，生产建设过程中的水土流失问题也愈加严重［1］，其中，生产建设项目产生的水土流失已经成为当前我国新增水土流失的主要策源地［2］。如水利建设、城镇开发、铁路公路建设、矿山开采等，常常对地表植被和地面造成不同程度的扰动，破坏了原始地貌，造成了新的、严重的水土流失，形成了独特的侵蚀特点［3－5］。孙飞云等［6］研究认为，在强降雨条件下，弃土场内的泥沙输移量是建设项目进行前的几十倍乃至上百倍。郭成久等［7］对弃土场侵蚀产沙过程的研究结果表明，产沙量随坡度和降雨强度的增大而增加，侵蚀量增加较快。徐永年等［8］通过研究各种土壤侵蚀影响因素，提出了新的水土流失预测方法。李强等［9］对煤田开发区的侵蚀产沙进行了研究，结果表明，扰动地面的土壤入渗率和径流量均大于原始地面。此外，国内一些学者［10－12］还对生产建设中扰动地面侵蚀产沙的影响因子、侵蚀过程、预测方法等进行了相应的研究，尽管取得了一些成果，但我国对生产建设人为活动水土流失过程、机制、预测预报及其侵蚀特殊性等方面的研究还十分薄弱［13］。笔者采用野外放水冲刷试验方法，通过模拟生产建设中扰动地面，探讨生产建设扰动地面的侵蚀过程及其机制，并对侵蚀产流产沙进行定量研究，以期为生产建设项目新增水土流失准确预测、科学配置水土保持措施、生态环境重建及科学合理编制水土保持方案提供理论依据。

1 试验设计与研究方法

1.1 放水试验设计

试验采用野外放水冲刷模拟的方法。共设计5种放水流量，分别为5、10、15、20 和25 L/min，3 个坡度级别，分别为5°、10°和18°。

1.2 样地选取

试验于2011 年6—8 月在野外进行，试验样地选取位于神木县西沟乡六道沟村的一块撂荒地坡面。因神府东胜煤田生产建设中造成的地面扰动情况复杂，真实扰动地面不能满足试验所需的水源、坡度、坡长等条件，因此，试验模拟的扰动地面是用铁锹将原始地面翻动20 cm 深，并将其平整后形成。试验区土壤物理性质见表1。

表1 试验区土壤物理性质Tab.1 Physical characteristics of soil samples

1.3 试验小区布设

试验小区为10 m×1 m 的长方形，两侧边界用1 mm 厚的钢板密封(插入地下0.15 m，地面露出0.1 m)。小区上方放置一个容积为2 m3的水箱，经水泵由水库供水。紧靠小区顶端布置一个嵌入地下与小区等宽、与坡面齐平的溢流箱，由汽油泵从水箱供水，并在汽油泵出水管口安装2 个闸阀以调节放水流量，确保试验水流是均匀的薄层水流。小区底端安置可嵌入地表的集流槽。依次在距离小区顶端2 ～3 m、5 ～6 m、8 ～9 m 处设置3 个观测断面。试验装置示意图见图1。

1.4 试验过程及数据采集

试验开始前，测定小区的土壤含水量、土壤密度、水流温度等，并对放水流量进行2 次率定，前后误差不超过5%。试验过程中，记录径流形成前时间并观测坡面微形态变化。当径流形成后，在小区集流槽出水口用集流桶收集径流泥沙样并记录采集时间，随后用量筒测量其体积。

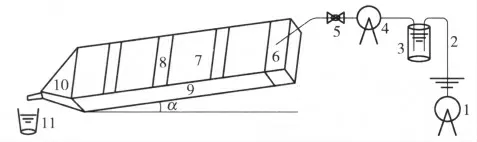
图1 野外放水冲刷试验装置示意图Fig.1 Sketch map of outdoor scouring erosion experimental apparatus

试验时间共45 min，产流初期每1 min 取1 次径流泥沙样，放水历时3 min 后，每隔3 min 取1 次径流泥沙样。同时，用高锰酸钾示踪法测量坡面上不同断面的径流平均流速，用薄钢尺测量坡面各断面水流宽度及径流深。各样品的含沙量采用烘干法测定。

1.5 土壤入渗率计算

下垫面不同，土壤水分入渗过程也不相同。一般而言，土壤入渗过程直接决定了产流过程和产流量。根据水分平衡公式可知，放水量为径流量、入渗量与蒸发量之和，由于水分蒸发量与径流量和入渗量相比很小，故忽略水分蒸发量。土壤入渗率为单位时间单位面积上土壤水分下渗量，可知，土壤入渗率公式［14］为

式中:i 为土壤入渗率，mm/min;W 为放水量，m3;R为径流量，m3;S 为小区水平投影面积，m2;t 为放水时间，min;1 000 为单位换算系数。

2 结果与分析

土壤侵蚀产沙主要是降水特征、下垫面状况等因素共同作用的结果。放水冲刷形成的径流不仅是引起坡面发生侵蚀的主要驱动力，而且是泥沙输移的载体。为了更直观地阐述径流冲刷对坡面侵蚀的微观机制，揭示不同坡面处理条件下坡面产流产沙在整场放水冲刷过程中随时间的动态变化过程，研究土壤入渗率、含沙量、土壤剥蚀率与放水流量和坡度之间的定量关系，笔者根据试验现场实测径流泥沙数据，通过数据处理分析，分别点绘出了不同下垫面坡面土壤入渗率、径流含沙量、土壤剥蚀率随时间的变化趋势图，见图2 ～图4。

图2 不同下垫面土壤入渗率随时间的变化Fig.2 Variation of soil infiltration rate over souring time under different underlying surface

图3 不同下垫面径流含沙量随时间的变化Fig.3 Variation of sediment concentration over souring time under different underlying surface

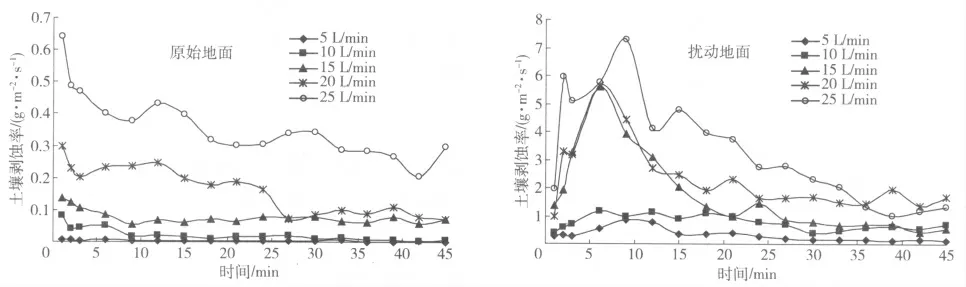
图4 不同下垫面土壤剥蚀率随时间的变化Fig.4 Variation of soil detachment rate over souring time under different underlying surface

2.1 土壤入渗率动态变化特征

由图2 可以看出:在不同的放水流量下，原始地面的土壤入渗率变化趋势较扰动地面平缓。扰动地面的土壤入渗率在1 ～9 min 内变化较为剧烈，呈急剧的下降趋势，土壤入渗率的减小幅度达38.53%～97.10%，随后则以平缓波动变化。不同放水流量下，原始地面的土壤入渗率变化范围为0.19 ～0.95 mm/min，其中，流量为20 和25 L/min 时的平均土壤入渗率较为接近，分别为0.58 和0.61 mm/min，其余放水流量下的平均土壤入渗率较为接近，变化范围在0.31 ～0.35 mm/min 之间;扰动地面土壤入渗率的变化区间为0.04 ～2.03 mm/min，各放水流量下的平均土壤入渗率不同，在0.14 ～0.51 mm/min 之间变化。对比可知，扰动地面平均土壤入渗率是原始地面的0.44 ～0.73 倍。利用SPSS 18.0对原始地面和扰动地面的平均土壤入渗率与放水流量进行回归拟合，得出经验方程如下。

原始地面:

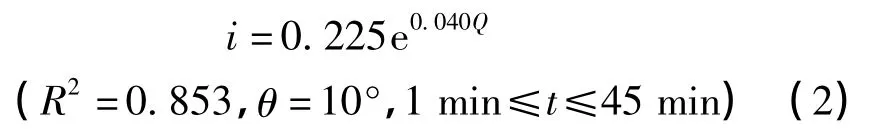
扰动地面:

式中:Q 为放水流量，L/min;θ 为坡度，(°) 。

回归方程(2)与(3)表明，原始地面的平均土壤入渗率随放水流量呈显著的指数函数关系，扰动地面的平均土壤入渗率与放水流量则呈显著的幂函数关系，二者的决定系数R2均在0.850 以上，Sig.值均小于0.05，回归效果显著。

结合现场观测分析可知，原始地面植被较好。Liu Guobin［15］对草地植被恢复的研究结果表明，根系层对土壤的缠绕、固结等作用强化了土壤的抗冲性，使土壤具有良好的结构和孔隙。如表1 所示，原始地面的平均土壤密度为1.53 g/cm3，较扰动地面(1.21 g/cm3)大，表明原始地面具有较强的抗蚀能力。扰动地面土壤疏松，土粒之间多存在较大孔隙，平均孔隙度为0.54，原始地面为自然状态，平均孔隙度为0.42;因此，当放水冲刷时水流首先入渗土壤，此时原始地面和扰动地面的土壤入渗率最大。随冲刷历时的延续，原始地面因土壤结构和孔隙度较好，地面细小碎散土粒较少，土壤入渗率在整个过程中变化趋势较为平缓，而扰动地面土壤多为大空隙且碎散土粒多，因大量细小土粒堵塞土壤大孔隙，故在9 min 前土壤入渗率急剧减小，最终趋于稳定。

2.2 不同放水流量下坡面侵蚀产沙特征

2.2.1 径流含沙量动态变化特征 径流含沙量的变化是侵蚀产沙过程的一个重要体现，是产流、产沙及水沙动态关系消长与演变的重要指标［16］。

从图3 可知:原始地面和扰动地面的径流含沙量均随时间呈逐渐减小趋势，且随着放水流量的增大，径流含沙量均增大。相同的放水流量下，原始地面平均径流含沙量的变化范围为1.61 ～12.05 g/L，扰动地面为62.16 ～118.66 g/L，扰动地面的平均径流含沙量是原始地面的10 ～39 倍。放水流量为5和20 L/min 时，原始地面的径流含沙量波动较为剧烈，在1 ～3 min 呈急剧减小趋势，其余则在1 ～9 min表现为急剧下降，随后径流含沙量随时间呈现平缓波动变化。扰动地面的径流含沙量在1 ～12 min 呈现出剧烈的多峰型波动状态，12 min 后各放水流量下径流含沙量相差变化不大，均表现为平缓减小的趋势。对原始地面和扰动地面的平均含沙量与放水流量分别进行相关分析，建立的经验关系式如下。

原始地面:

扰动地面:

式中Sw为径流含沙量，g/L。

通过式(4)与(5)可知，原始地面的平均径流含沙量随放水流量呈指数函数关系，扰动地面的平均含沙量与放水流量呈对数函数关系，二者的决定系数R2均在0.980 以上，Sig.值均小于0.001，回归效果达到极显著水平。

经分析可知:原始地面具有密实的土壤结构和良好的土壤孔隙度(表1)，因此，土壤抵抗径流的冲刷能力较强，且因原始地面具有细小的碎屑土壤颗粒，产流初期首先被冲刷运移;所以此时径流含沙量最大。对于扰动地面，由于土壤的稳定结构被破坏，地表碎屑土粒增多，且土粒大小不均一，土壤抗蚀能力差，径流初期就能形成较大的含沙量。随着冲刷历时的推移，原始地面和扰动地面均有不同程度的跌坎形成，并逐渐贯通形成结构较为稳定的细沟，此时径流含沙量趋于稳定。

2.2.2 土壤剥蚀率动态变化特征 从图4 可以看出:总体趋势上，原始地面与扰动地面的土壤剥蚀率均随放水流量的增大而增大，并随时间呈现出平缓或剧烈的上下波动直至达到某一稳定状态。此外，在相同的放水流量下，扰动地面的平均土壤剥蚀率(19.38 ～202.58 g/(m2·s))远大于原始地面(0.24 ～21.75 g/(m2·s))，其平均土壤剥蚀率是原始地面的9 ～79 倍，其中5 L/min 放水流量情况下，甚至达到79 倍左右。由此可知，人为对地面的扰动加剧了土壤侵蚀的发生。通过比较可知:1 ～9 min 原始地面的土壤剥蚀率急剧减小，随后出现了不同程度的波动;但总体趋于平缓，其中20 和25 L/min 放水流量情况下，土壤剥蚀率在9 min 后呈现出较为强烈的波动。可知，随着放水流量的增大，径流量、径流深、流速均增大，径流具有较大的侵蚀动能及搬运能力，冲刷能力强，土壤剥蚀率大。扰动地面的土壤剥蚀率表现为先增大后减小，并逐渐趋于平缓的趋势，其中5 和25 L/min 放水流量情况下，土壤剥蚀率在9 min 时达到最大，其余均在6 min 时达到最大，15、20和25 L/min 放水流量情况下，土壤剥蚀率均表现为较强烈的波动减小趋势。分析原因，可能是产流初期径流量小，一部分径流入渗土壤，径流所能挟带的泥沙含量少，随着历时的延续，土壤入渗率减小，用于形成径流的水量增加，且形成的细沟结构不稳定，土壤剥蚀率增大。

经回归拟合，原始地面与扰动地面平均土壤剥蚀率与放水流量的经验关系式如下。

原始地面:

扰动地面:

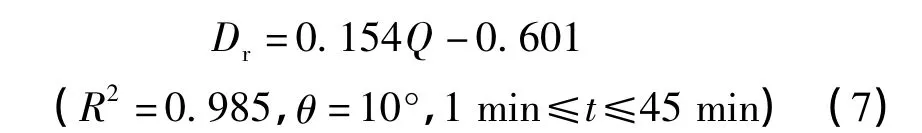
式中Dr为土壤剥蚀率，g/(m2·s)。

可以看出，原始地面的平均土壤剥蚀率与放水流量可以用指数函数进行描述，扰动地面则表现为显著的线性相关关系。

2.3 不同坡度下坡面侵蚀产沙特征

根据试验现场实测径流泥沙数据，分别点绘了不同坡度下径流含沙量、土壤剥蚀率随时间的变化趋势，见图5 ～图6。

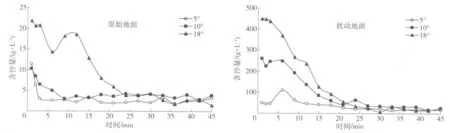
图5 不同下垫面径流含沙量随时间的变化Fig.5 Variation of sediment concentration over souring time under different underlying surface

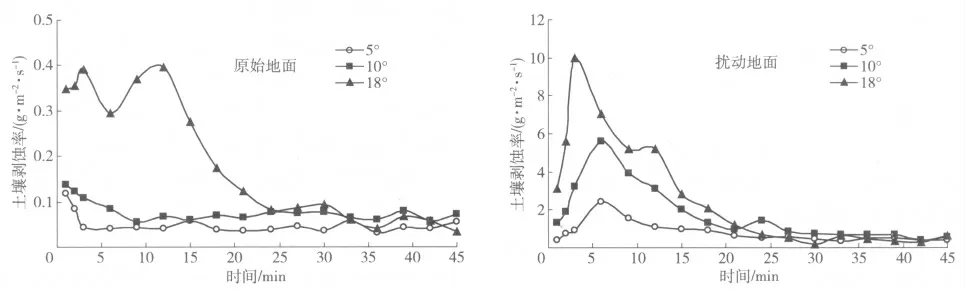
图6 不同下垫面土壤剥蚀率随时间的变化Fig.6 Variation of soil detachment rate over souring time under different underlying surface

2.3.1 径流含沙量动态变化特征 由图5 可知:不同下垫面的径流含沙量均随着坡度的增大而增大，并随冲刷历时呈现不同程度的波动减小趋势，进而趋于稳定波动状态。原始地面坡度为5°和10°，扰动地面为5°时，径流含沙量在1 ～9 min 内变化较为剧烈，之后趋于稳定。原始地面坡度为18°，扰动地面为10°和18°时，径流含沙量则在24 min 前呈现急剧减小趋势。分析原因，可能是小的坡度下，径流具有较小的动能，侵蚀能力较弱，细沟形成的结构稳定且规模较小，表现为缓慢的侵蚀演变过程;因原始地面土壤结构良好，坡度为10°时，径流含沙量(对比扰动地面)表现为平缓的波动状态。随着坡度增大，径流动能变大，侵蚀能力变强，细沟形成较快，但初期结构不稳定，随历时延续(24 min 时)，细沟规模及径流含沙量逐渐趋于稳定。原始地面的平均径流含沙量变化范围为3.27 ～9.62 g/L，扰动地面为36.19 ～155.96 g/L，不同坡度下扰动地面的平均径流含沙量是原始地面的11 ～23 倍。

通过回归模拟，建立的平均径流含沙量随坡度的经验方程如下。

原始地面:

扰动地面:

回归方程式(8)和(9)表明，原始地面的平均径流含沙量是坡度的指数函数关系式，扰动地面的平均径流含沙量与坡度呈现为显著的线性函数关系。

统计分析(R2＞0.96)结果说明，坡度对径流含沙量具有显著的影响。

2.3.2 土壤剥蚀率动态变化特征 由图6 可知:不同下垫面土壤剥蚀率均随坡度的增大而增加，原始地面在坡度为5°和10°时，土壤剥蚀率随时间呈现出先减小(9 min 前)后趋于平稳波动的变化趋势，坡度为18°时，在1 ～24 min 内土壤剥蚀率随时间波动剧烈，12 ～24 min 内土壤剥蚀率急剧减小并逐渐趋于稳定;而扰动地面的土壤剥蚀率均呈现为先增大后减小的单峰变化过程，且峰值出现在6 min 左右。经比较，原始地面的平均土壤剥蚀率变化范围为0.05 ～0.19 g/(m2·s)，扰动地面为0.79 ～2.70 g/(m2·s)，不同坡度下扰动地面的平均土壤剥蚀率是原始地面的14 ～22 倍。分析可知:坡度较小时，坡面径流的流速、流量较小，径流侵蚀能力和挟沙能力小，土壤剥蚀率小;坡度增大，径流流速、流量均增大，径流侵蚀能力和挟沙能力变大，土壤剥蚀率变大。通过对原始地面和扰动地面土壤剥蚀率与坡度进行回归分析，建立的二者之间的经验关系式如下。

原始地面:

扰动地面:

可以看出，原始地面的平均土壤剥蚀率与坡度呈现显著的指数函数关系，扰动地面的平均土壤剥蚀率与坡度则为显著的线性相关。

2.4 不同下垫面平均土壤剥蚀率与放水流量和坡度的关系

为了探讨不同下垫面处理条件下土壤剥蚀率与放水流量和坡度之间的定量关系，利用SPSS 18.0对相关数据进行了回归拟合分析。结果表明，不同放水流量情况下，原始地面和扰动地面的土壤剥蚀率与放水流量和坡度呈显著的复合幂函数关系。数据样本方差决定系数R2均大于0.896，显著性水平Sig.值均小于0.01。通过比较表2 中原始地面与扰动地面各回归关系式的显著性水平可知，土壤剥蚀率受放水流量和坡度的共同影响。

表2 土壤剥蚀率与放水流量和坡度的回归方程Tab.2 Regressive equations between soil detachment rate with flow discharge and slope gradient

3 结论

1) 不同放水流量情况下，平均土壤入渗率原始地面＞扰动地面。原始地面与扰动地面的平均土壤入渗率与放水流量分别呈显著的指数函数和幂函数关系。

2) 原始地面和扰动地面的径流含沙量及土壤剥蚀率均随放水流量和坡度的增大而增大，随放水历时延续逐渐减小并趋于稳定。扰动地面的平均径流含沙量及土壤剥蚀率远大于原始地面。原始地面平均径流含沙量及土壤剥蚀率与放水流量、坡度呈显著的指数相关关系。扰动地面的平均径流含沙量与放水流量呈显著的对数函数关系，与坡度呈线性关系，其平均土壤剥蚀率与放水流量和坡度分别呈显著的线性关系。

3) 原始地面和扰动地面的平均土壤剥蚀率与放水流量和坡度呈复合幂函数关系，土壤剥蚀率由放水流量和坡度共同影响。

［1］ 冷疏影，冯仁国，李锐，等.土壤侵蚀与水土保持科学重点研究领域与问题［J］.水土保持学报，2004，18(1):1－6

［2］ 林敬兰，朱颂茜，温秀萍，等.开发建设项目土壤侵蚀监测方法体系探讨:以福银高速公路联合段为例［J］.亚热带水土保持，2010，22(4):47－51

［3］ 赵永军.开发建设项目水土保持方案编制技术［M］.北京:中国大地出版社，2006:38

［4］ 陈晶萍.工程侵蚀的根源及其防治技术措施体系［J］.福建水土保持，2001(2):48－51

［5］ 王海军，张雨华，王兆良，等.编制矿山开发建设项目水土保持方案的几点经验［J］.水土保持通报，2005，25(5):108－110

［6］ 孙飞云，杨成永，黄新民，等.铁路工程建设水土流失监测试验研究:以北同蒲增建二线改造项目太原至原平段为例［J］.水土保持研究，2006，13(1):248－250

［7］ 郭成久，安晓奇，武敏，等.弃土场侵蚀产沙模拟试验研究［J］.中国水土保持，2010(3):29－31

［8］ 徐永年，孙秋来.谈开发建设项目扰动面土壤流失量的预测［J］.中国水土保持，2004(3):25－27

［9］ 李强，李占斌，鲁克新，等.神府东胜矿区不同下垫面产流产沙试验研究［J］.水土保持研究，2008，15(3):1－3

［10］孙虎，唐克丽.城镇建设中人为弃土降雨侵蚀实验研究［J］.土壤侵蚀与水土保持学报，1998，4(2):29－35

［11］吴普特，周佩华.黄土坡面薄层水流侵蚀试验研究［J］.水土保持学报，1996，10(1):40－45

［12］王利军，鲍永刚.北京市不同地貌类型开发建设项目新增水土流失预测方法研究［J］.北京水务，2008(2):48－51

［13］贺秀斌，陈晨宇，韦杰，等.工程建设弃土弃渣水土流失7Be 核素示踪监测技术［J］.水土保持通报，2006，26(6):67－71

［14］马萍，宋锋惠，史彦江，等.伊犁河流域裸露缓坡地放水试验研究［J］.中国水土保持科学，2010，8(1):34－39

［15］Liu Guobin.Study on soil anti－scourability and its mechanism of grassland on Loess Plateau［J］.Journal of Soil Erosion and Soil and Water Conservation，1998(1):93－96

［16］马春艳，王占礼，寇晓梅，等.工程建设弃土弃渣水土流失过程试验研究［J］.水土保持通报，2009，29(3):78－82