下丘脑－垂体－肾上腺轴激素分泌的周期振荡及混沌现象

佟 倜，巴合提古丽·阿斯里别克，孙迎春

（1.吉林大学第二医院胸外科，吉林长春 130041；2.东北师范大学物理学院，吉林长春 130024；3.新疆伊犁师范学院电子与信息工程学院，新疆伊犁 135000）

下丘脑－垂体－肾上腺轴激素分泌的周期振荡及混沌现象

佟 倜1，巴合提古丽·阿斯里别克2，3，孙迎春2

（1.吉林大学第二医院胸外科，吉林长春 130041；2.东北师范大学物理学院，吉林长春 130024；3.新疆伊犁师范学院电子与信息工程学院，新疆伊犁 135000）

结合生理学内分泌调节理论，采用了变步长龙格－库塔法，以Matlab软件为计算平台，对改进的下丘脑－垂体－肾上腺轴激素脉冲分泌的非线性动力学进行了参变量数据模拟，求出了下丘脑－垂体－肾上腺轴激素脉冲分泌的周期振荡解及混沌解.结果显示，此分泌系统中激素浓度变化与实验事实相符，其混沌模型是合理的.

下丘脑－垂体－肾上腺轴；非线性动力学模型；脉冲分泌；混沌；周期振荡

下丘脑－垂体－肾上腺轴是人体内分泌系统中相对独立的循环系统之一，在机体的生理过程中起着重要作用.它与神经系统等相互作用，调节、维持机体生理代谢的内环境稳定，对人的生长发育非常重要［1］，我们在人体生理的多个系统中建立并分析了非线性动力学模型［2－3］.下丘脑－垂体－肾上腺轴主要调节血液中皮质醇激素的分泌.本文依据下丘脑－垂体－肾上腺轴各激素间的相互作用关系，在已有模型基础上［4－5］，依据生理学理论，考虑了更多的调节因素，改进了原有模型，并以Matlab软件为计算平台，对此模型系统内各参数进行合理调节，从而探讨激素分泌的相关性，以期对人体的内分泌活动规律和功能给予理论上的深入研究，并对临床病例分析和诊断提供分析参考数据.

1 非线性动力学方程

分泌肾上腺皮质激素的过程主要有：在垂体分泌的促肾上腺激素（ACTH）作用下，通过由胆固醇参与的酶促反应形成；机体自身能产生少量的自主分泌（autonomors secretion）；下丘脑分泌的促皮质激素释放激素（CRH）也具有激活作用；血液中自由的皮质醇对下丘脑和垂体有负反馈作用；血液中皮质醇的浓度可由从结合态皮质醇中解离出来.

事实上，通过生理学测定早已发现，ACTH和皮质醇在血液中的浓度既有昼夜节律，又有1～3 h的脉冲释放现象，同时，非线性动力学理论认为［6－7］，正常情况在血液中激素的脉冲分泌并不是均匀的，而是在一个有限宽度的区间做非均匀振荡，即呈现混沌现象.考虑到此轴内各个激素间的相互作用，加入体现相互作用的交叉项，以期通过对改进模型的求解，能解释激素分泌中的振荡现象及混沌现象.

模型方程为：

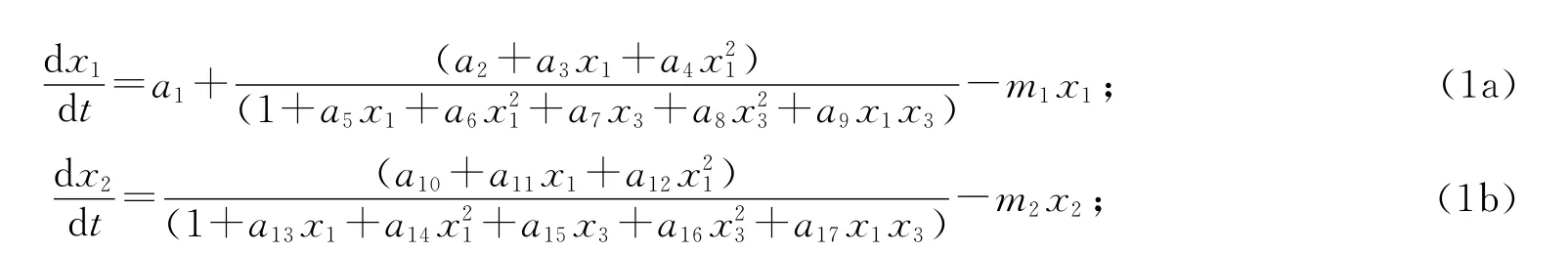
方程组（1a）－（1e）中x1，x2，x3，x4和x5分别表示CRH、ACTH、游离皮质醇（cortisol）（包括糖皮质醇和盐皮质醇）、与皮质类固醇结合的球蛋白（CBG）结合皮质醇和与白蛋白（ALB）结合皮质醇的血浆浓度，各激素单位都是μg／L，时间单位是min.式中各参数的意义：ai表示各个因子的相对作用强度，是正的常数项；mi是代谢清除系数，表达了激素浓度的衰减，体现了体内的正常代谢；单独的常数项表示腺体的自主分泌（autonomous secretion）；a1是下丘脑以外的释放激素分泌源的分泌强度，包括了神经系统对CRH分泌的影响；dx i／dt表示x i随时间变化的动力学演化规律.由于各个方程中分式的分子或分母的所有系数均为正数，根据代数方程的理论可知［3］：此非线性方程组没有正的实数解，但x i表示的是血液中皮质醇激素的浓度，且都为正值，因此实际模型的方程组中，分式的分子无极点，分母无奇点.这就保证了模型中分式不存在奇点发散的情形.在动力学演化的过程中，各方程中的分式与清除项一直处于竞争状态，代谢清除是以指数衰减的方式进行，在暂态过程中处于主导地位.整个方程组中分式项具有非线性特征，它与清除项共同作用可以维持系统处于周期振荡或混沌状态.

为了便于模型的分析，对上面的方程组进行数学化简.令：

2 求解方程

2.1 均匀的振荡解

方程组共有36个未知系数，依据现有数学理论无法求解出确切的解析解.此模型是36维的参数空间，是高度非线性的分时微分方程组，以常规的数学方法（如阻尼最小二乘法，回归法等）无法解出方程确定的系数，因此采用Matlab软件，并利用四阶龙格－库塔数值积分法，对方程组（2a）－（2e）进行代数变换，求出了周期振荡解（见方程组（3a）－（3e））及其在给定初始条件情况下数值解的时域图（见图1）.

图1 激素脉冲分泌的均匀振荡时域图

由图1可得各激素分泌x1，x2，x3和x4的振荡周期均为181.8 min，相应的振荡基础值分别为0.006 7，0.036 9，5.126 6和85.002 9μg／L，与生理实验测定数据符合较好，从而说明该模型是合理模型.

2.2 混沌解

对均匀振荡解方程组的系数进行更细致的调节，得到了具有混沌特征的方程参数，代入方程组，结果如（4a）－（4e）式：

选取实验测定值（x10＝0.01，x20＝0.05，x30＝12.5，x40＝82，x50＝19）为初值，代人方程组（4a）－（4e）中进行求解数值解，得到血液中激素浓度与时间关系的时域图（见图2）.图像表面，经过短暂的暂态过程后，各激素的浓度都在做非周期振荡，且峰值既不相等又不超出周期振荡显示的峰值，体现出混沌特征.

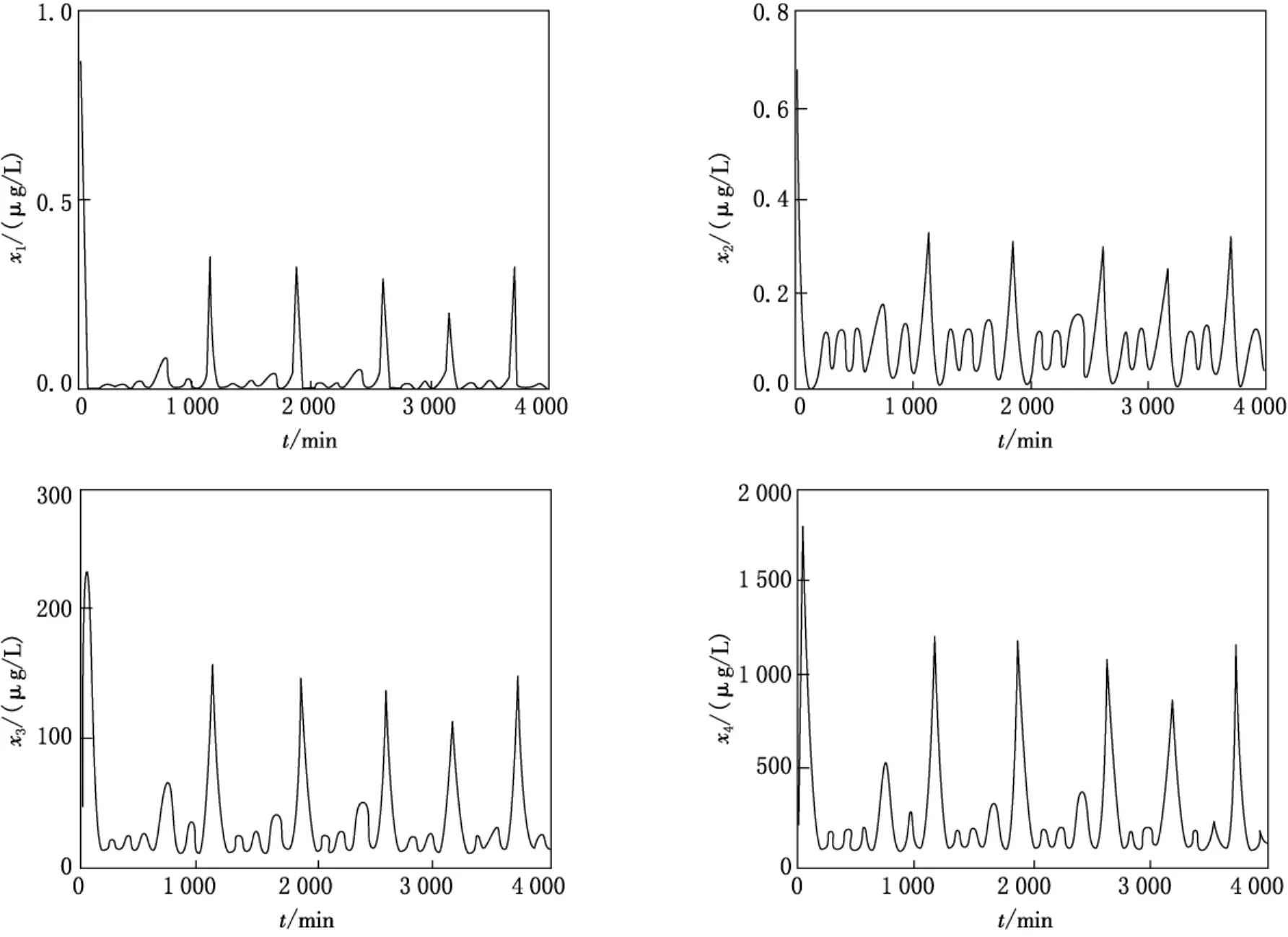
图2 各激素具有混沌特性的时域图

2.3 混沌相图及吸引子

为了进一步确定方程组（4a）－（4e）具有混沌特性，用Matlab软件计算出激素分泌的相图（以x1为例，见图3），图像清楚显示出从1周期、3倍周期到6倍周期，直至混沌的过程.相图中的每一点都代表系统的一个状态，单倍周期相图是一个闭合的曲线，表示系统是在做周期运动，即时域图中的周期振荡.2倍周期相图则为有一个交叉点的2个闭合曲线，依此类推，混沌状态时的相图为具有单一节点的无穷多闭合曲线的集合，此节点即为混沌的吸引子.

图3系统各周期相图及混沌吸引子

3 结束语

迄今为止人们认为混沌现象至少有以下3个特征：

（1）混沌运动是决定性和随机性的对立统一，即它具有随机性但又不是真正的或完全的随机运动；

（2）混沌现象对初始状态的依赖非常敏感，即具有蝴蝶效应；

（3）只有非线性系统才可能做混沌运动.

本文对下丘脑－垂体－肾上腺轴激素分泌的研究表明，此系统内激素是以从周期振荡到倍周期运动直到混沌运动的过程，合理的描述了激素之间的相互作用和转化，通过合理调整参数，得到了激素分泌的混沌解.

［1］特纳·贝格纳尔.普通内分泌学［M］.北京：科学出版社，1983：235－256.

［2］王颖，孙迎春，佟倜.下丘脑－胰岛轴血糖调节的非线性动力学模型［J］.东北师大学报：自然科学版，2010，42（1）：133－136.

［3］王颖，佟倜，孙迎春.下丘脑－垂体－睾丸轴激素的振荡行为与非线性动力学模型［J］.东北师大学报：自然科学版，2009，41（2）：92－95.

［4］LIU YI－WE1，HU ZHI－HONG.A dynamical model for the pulsatile secretion of the hypothalamo－pituitary－adrenal axis［J］.Mathematical and Computer Modeling，1999，29：103－110.

［5］LIU B Z，DONG G M.A improved mathematical model of hormone secretion in the hypothalamo－pituitary－gonadal axis in man［J］.J Theor Biol，1991，150（51）：323－326.

［6］刘秉正.非线性动力学与混沌基础［M］.长春：东北师范大学出版社，1994：301－407.

［7］刘秉正.生命过程中的混沌［M］.长春：东北师范大学出版社，1999：162－178.

Periodic oscillation of the hormone secretion of hypothalamus－pituitary－adrenal cortex axis and chaos

TONG Ti1，BAHETIGULI·Asilibieke2，3，SUN Ying－chun2

（1.Department of Thoracic Surgery of No.2 Hospital，Jilin University，Changchun 130041，China；2.School of Physics，Northeast Normal University，Changchun130024，China；3.College of Electronic and Information Engineering，Yili Normal University，Yili 135000，China）

In this paper，the periodic oscillation and the chaos solution of an improved model for the hormone secretion of the hypothalamus－pituitary－adrenal axis was proposed.This model is based on Physiology endocrine regulation theory and used Matlab working platform and the four order Runge－Kutta（RK4）method to simulate a group of parameter data which fit the model.The results showed that the all changes with time of the concentrations of the hormones in the model agree well with experimental results.From the results，the model is a more reasonable one.

hypothalamus－pituitary－adrenal cortex axis；nonlinear dynamics model；pulsatile secretion；chaos；periodic oscillation

Q 45

110·5110

A

1000－1832（2011）04－0076－05

2011－05－08

吉林省科技发展计划项目（20030543－3）.

佟倜（1962—），男，教授，博士研究生导师，主要从事胸外科临床及基础研究；通讯作者：孙迎春（1961—），女，副教授，主要从事生物物理研究.

石绍庆）