基于VAR和VEC模型的杭州市三次产业结构分析

阳长征

（桂林理工大学管理学院，广西 桂林 541004）

基于VAR和VEC模型的杭州市三次产业结构分析

阳长征

（桂林理工大学管理学院，广西 桂林 541004）

通过对过去文献的综述，鉴于传统的经济建模方法分析及存在的不足，结合经济计量分析的特点，提出了基于向量自回归（vector auto regression，VAR）及向量误差修正（vector error correction，VEC）模型的经济数据的分析方法，阐述了该方法在经济计量分析中的优点，并介绍了VAR和VEC的模型构建。通过杭州市1978—2008年三次产业数据的实例分析，揭示了杭州市三次产业之间的关系，其分析结果与杭州实际状况相吻合，具有指导意义，能为国家或地区的政策制定和投资策略指明方向。

产业结构；向量自回归；修正模型；实证检验

1 引言

过去有很多学者采用不同方法对中国产业结构问题做过研究。但从现有文献来看，他们采用的方法几乎都是以经济理论为基础来描述经济变量之间的结构关系，这些模型的优点是具有明显的经济理论含义。但是，从计量经济学建模理论而言，也存在许多不足和缺陷：通常明确哪些是内生变量、哪些是外生变量，并不容易，甚至往往带有主观性。如果在一组变量之中有真实的联立性，那么这些变量就应平等地加以对待，而不应该事先区分内生和外生变量。内生变量与扰动项相关，从而使模型参数估计变得十分复杂，也不能很好地反映出变量间的动态联系。在借鉴现有文献研究的基础上，以及针对过去常使用的研究方法存在的不足，本文通过VAR和VEC模型对三次产业结构进行分析，为我国或地区产业结构布局的调整和优化提供依据。该模型与过去研究方法相比具有如下3个的优点：第一，它不是以经济理论为基础描述经济变量之间的结构关系来建立模型的，而是以数据统计性质为基础，把某一经济系统中的每一变量作为所有变量的滞后变量的函数来构造模型；第二，它是一种处理具有相关关系的多变量的随机扰动对系统的动态冲击的最有效的方法。而且在一定条件下，多元移动平均（moving average，MA）模型、自身回归移动平均（autoregressive moving average，ARMA）模型，也可化为VAR模型来处理，这为研究具有相关关系的多变量的分析和预测带来很大方便；第三，VAR模型所表述的是变量之间的一种“长期均衡”关系，而实际经济数据却是“非平衡过程”的时间序列，即在现实经济模型估计中各变量之间常常存在协整关系，因此向量误差修正模型VEC能用数据的动态非均衡过程来逼近经济理论的长期均衡过程［1］。

2 模型构建

2.1 VAR和VEC模型

向量自回归（VAR）是基于数据的统计性质建立模型，它把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型，从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型。Y（t）=A（1）Y（t-1）+…A（n）Y（tn）+BX（t）+e（t），其中（t）是一个内生变量列向量，X（t）是外生变量向量，A（1），……，A（n），和B是等估的系数矩阵，e（t）是误差向量。误差向量内的误差变量之间允许相关，但是这些误差变量不存在自相关，与Y（t），Y（t-1），……，Y（t-n）和X（t）也不相关。

Engle和Granger指出两个或多个非平稳时间序列的线性组合可能是平稳的，假如这样一种平稳的或I（0）的线性组合存在，这些非平稳（有单位根）时间序列之间被认为是具有协整关系的。这种平稳的线性组合被称为协整方程且可被解释为变量之间的长期均衡关系。

向量误差修正模型 （VEC）是一个有约束的VAR模型，并在解释变量中含有协整约束，因此它适用于已知有协整关系的非平稳序列。

2.2 建模步骤

第一，对数据进行趋势分析、滞后排除项检验以及滞后长度选择标准分析，从而进行VAR模型估计。

第二，检验变量之间的因果关系。Granger因果检验是用于检验两个变量之间因果关系的一种常用的方法，它可以更准确地研究经济变量之间的相关关系，避免虚假回归。Granger因果关系是一个特定的当期变量与另一变量集之间所有过去信息之间的关系，即若一个变量X的滞后值在对另一个变量Y的解释方程式中是显著的，那么就称X是Y的“格兰杰原因”。

第三，进行变量间的冲击响应和预测误差的方差分解分析。由于VAR模型是一种非理论性模型，它无需对变量做任何先验约束，在分析VAR模型时，往往不是分析一个变量的变化对另一个变量的影响如何，而是分析当一个误差项发生变化，或者说模型受到某种冲击时对系统的动态影响，这种分析方法称为脉冲响应函数方法。而方差分解是分析每一个结构冲击对内生变量变化（通常用方差来度量）的贡献度如何。

第四，在VEC模型估计前，先对经济序列进行平稳性检验。实际中，只有极少数时间数据是平稳的。当采用时间序列模型时，所用时间序列应具有平稳性，但是经济变量往往非平稳，用非平稳变量建立回归模型会带来伪回归问题，因此在进行协整分析之前，首先对各经济变量进行单整检验，分析各经济变量的平稳性，如不平稳则通过差分使其变为平稳的时间序列。

第五，对于其中的非平稳性变量进行协整检验以及误差修正，从而进行VEC模型估计［2］。

3 实证分析

3.1 数据来源

该实例分析的数据来自 《杭州市年鉴》（1978—2008年）［3］，其中的指标分别为三次产业产值总值及总值指数（即设定1978年的水平为100，将各年产值与1978年相比所得的指数）。其中Y1，Y2，Y3分别为第一产业、第二产业、第三产业产值指数序列，这些数据是经过适当处理后得到的。在此采用E-views 6.0软件进行数据处理。

3.2 VAR模型

（1）模型估计。

为了减少数据的波动，先对三次产业的产出指数序列Y1，Y2，Y3取自然对数，得到新的序列LY1， LY2，LY3，同时对取对数后的序列进行ADF单位根平稳性检验，可知VAR模型中应该包括截距项和趋势项。

对于所估计的VAR模型进行滞后长度选择标准分析，根据AIC信息准则（aic information criterion）和SC准则取最小值的原则来确定模型的滞后阶数。其处理结果显示，当选择3阶进行VAR模型估计比较理想。根据VAR模型参数估计结果，可以写出VAR模型的估计结果：

VAR模型的检验结果显示，所估计的VAR模型中3个方程的拟合优度R2都很大，几乎接近数值1，同时AIC准则和SC准则都比较小，说明该模型的估计比较合理［4］。

（2）Granger检验和滞后项检验。

对于杭州三次产业之间的因果方向检验，即判断各产业之间的因果关系，采用非平稳序列下的格兰杰（Granger）因果关系检验法进行分析检验。

格兰杰因果检验结果表明，在Y1方程中，Y2，Y3及这两变量所有滞后联合的格兰杰因果检验的概率值Prob.均小于5%的显著水平，则拒绝原假设，可以认为Y2，Y3及这两变量所有滞后联合是Y1的原因，表明第二、三产业的发展是第一产业发展的原因，说明杭州的工业和服务业的发展对农业的发展起很大的推动作用。关于Y2方程，Y1，Y3及这两变量所有滞后联合的格兰杰因果检验的概率值Prob.均大于5%的显著水平，则不能拒绝原假设，可以认为Y1，Y3及这两变量所有滞后联合不是Y2的原因，表明第二产业外生于系统，说明杭州的第二产业很发达，在很大程度上不依赖于当地的农业和服务业发展程度。关于Y3方程，Y1的格兰杰因果检验的概率值Prob.大于5%的显著水平，则不能拒绝原假设，可以认为Y1不是Y2的原因，而Y2及Y1和Y2这两变量所有滞后联合的格兰杰因果检验的概率值Prob.均小于5%的显著水平，则拒绝原假设，可以认为Y2及Y1和Y2这两变量所有滞后联合是Y1的原因，表明杭州服务业的发展很大程度上不依赖于农业的发展，但工业的发展和工业与农业的联合作用会影响服务业的发展。这些结果与杭州的经济发展实际情况相吻合［5］。

（3）脉冲响应函数与方差分解。

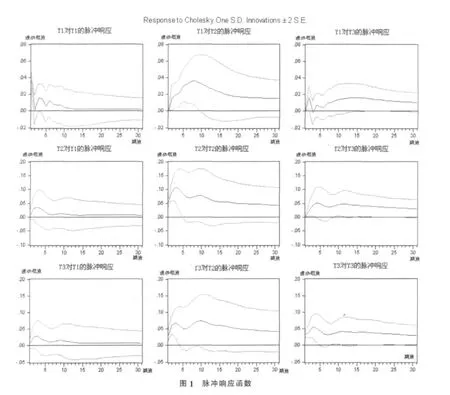
①脉冲响应函数分析。

由图1a～图1c可知：第一产业对来自自身的扰动立即做出了正向响应，其影响在前13期内会上下波动，于第13期后开始趋于稳定并持续增长，以及对第二产业第三产业的扰动作出的响应在第一期等于零，之后开始出现正向响应，直至第20期开始趋于稳定并持续增长。由图1d～图1f可知：第二产业对来自第一产业的冲击立即做出正向响应，于第15期后开始趋于稳定而持续的增长，而对于来自本身的冲击立即做出正向响应，接着缓慢上升至第3期，之后开始缓慢下降，对第三产业的冲击没有立即做出响应，而是缓慢上升至第3期，其后开始缓慢下降。由图1g～图1i可知：第三产业对来自自身和其他两个产业的冲击立即做出正向响应，之后正向波浪型变化，直至第10期开始缓慢下降。

②方差分解分析。

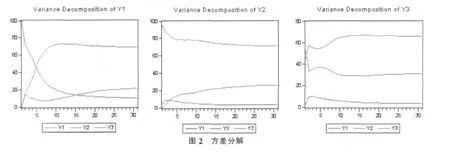
为了确定三次产业之间相互影响的程度，在此继续做方差分解分析，其分析结果如图2所示。

由图2可以看出：随着预测期的推移，第一产业预测方差中由第一产业自身扰动所引起的部分的贡献率一直缓慢下降至31期9.89%，第二产业对此的贡献率缓慢上升至13期的73.00%再下降至31期69.02%，第三产业对此的贡献率迅速上升至第2期14.45%再缓慢下降至第6期6.75%，之后再持续上升至第32期21.08%。在第二产业预测方差中由第二产业自身扰动所引起的部分的贡献率一直缓慢下降至第31期70.99%，第一产业对此的贡献率缓慢上升至第2期的33.38%再上升至第5期37.30%，第三产业对此的贡献率一直缓慢上升至第31期26.02%。在第三产业预测方差中由第三产业自身扰动所引起的部分的贡献率迅速下降至第2期70.99%，再缓慢下降至30期30.91%，第一产业对此的贡献率迅速上升至第3期的9.72%，再持续下降至31期3.12%，第二产业对此的贡献率首先迅速上升至第2期57.24%，再缓慢下降至第4期54.56%，再缓慢上升至第18期66.70%，其后基本持平［6］。

3.3 VEC模型

（1）单根检验。

由ADF单根检验结果可以看出：序列LY1，LY3，LY3的单根检验的统计量均大于10%检验水平下的临界值，因此这3个序列都包含单位根，从而是非平稳序列。序列LY1，LY3的一阶差分的单位根检验的概率值小于1%的显著水平，于是可以拒绝原假设，接受不存在单位根的结论，因此可以确定序列LY1，LY3一阶单整序列I（1）。而序列LY2直到二阶差分的单位根检验概率值才小于1%的显著水平，于是可以拒绝原假设，接受不存在单位根的结论，因此可以确定序列LY2是二阶单整序列I（2）。

（2）协整检验。

由协整检验可知：不论是迹检验还是最大特征值检验，检验的结果都是拒绝“至多存在1个协整关系”的原假设，而不能拒绝“至多存在2个协整关系”的原假设，因此表明在5%的水平下存在2个协整关系。

（3）VEC模型估计及分析。

依输出结果可以写出两个协整方程：（1）LY1t-1= 0.355LY3t-1+2.807；（2）LY2t-1=1.052LY3t-1-0.44，协整方程（1）说明在其他条件不变的情况下，第三产业的Ln（Y3）值每增加1个百分点，则第一产业的Ln（Y1）值就增加0.355个百分点，统计量显著，说明第三产业对第一产业有促进作用。协整方程（2）说明在其他条件不变的情况下，第三产业的Ln（Y3）值每增加1个百分点，则第二产业的Ln（Y1）值就增加1.052个百分点，统计量显著，说明第三产业对第二产业有促进作用。根据VEC模型的参数估计结果可得如下的修正模型：

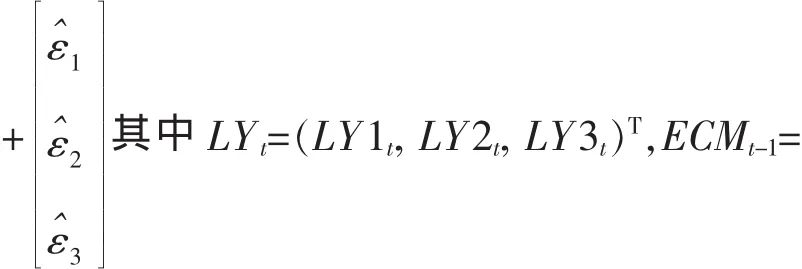
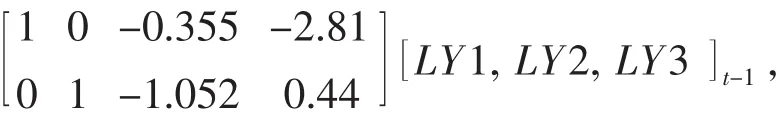
模型检验部分数据显示，VEC模型中3个方程的拟合优度R2都不小，同时AIC准则和SC准则分别为-9.837和-7.821，都比较小，说明该模型的估计比较合理。

协整关系图表明第一产业与第三产业之间的关系一直有所波动，至1988年趋于稳定，其后继续波动，2000年又趋于均衡稳定，2001—2008年虽然存在波动但波动幅度较小。同时第二产业与第三产业之间的关系一直存在较大波动，至1985年趋于稳定，其后继续波动至 1995年又趋于均衡稳定，1996—2008年虽然存在波动但波动幅度较小［7］。

4 结论和建议

（1）从上述分析可知三次产业结构失衡，主要表现为第二产业与第三产业发展不协调，其主要原因可能是投资与消费、基础工业与加工工业和基础设施之间的不协调；固定资产投资规模仍然过大，增长速度仍然过快，一些行业和地区低水平重复建设还没有得到有效遏制；资源瓶颈约束仍然很突出，能源、运输和重要原材料的供求形势依然紧张；价格上涨压力依然很大；就业压力并未缓解等。同时经济增长方式仍很粗放，基本上是速度型效益的表现，这可能是部分生产资料行业价格大幅度上涨和规模扩张效益大幅度上升拉动的结果。

（2）要按照以产业结构调整带动经济发展方式转变的理念，坚持增量做优与存量调整相结合，坚持企业搬迁与技术改造相结合，坚持外延式发展与内涵式发展相结合，把打造产业链和现代产业集群放到长三角整体发展中去谋划，加快调整优化产业结构和产业布局，努力推动三次产业联动发展。

（3）要坚持“工业兴市”不动摇。当前和今后一个时期,工业仍然是杭州经济的主要支撑、财政税收的主要来源、吸纳就业的主要渠道、推进城市化的主要动力，要大力提升改造传统优势产业，做强做大高新技术和战略性新兴产业。

（4）要加快发展现代服务业和文化创意产业。在当前和未来的经济中，服务业是增长最快的产业，要积极构筑与“生活品质之城”相适应的“高增值、强辐射、广就业”的现代服务业体系，要以现代服务业集聚区为依托，通过放宽市场准入，完善投融资体制，加强用地保障，落实税费减免优惠，鼓励主辅业分离。

（5）把加强宏观调控作为更好地调整结构、深化改革和转变增长方式的契机和手段，把宏观调控的着力点放在深化改革、调整结构、转变增长方式上，标本兼治；加快投资体制的改革步伐，协调推进其他方面的改革，包括金融体制的改革、企业兼并方面的政策，从而使总量政策、结构政策和改革政策形成一种合力；把扩大内需方式从投资转向消费，进一步鼓励消费增长［8］。

［1］高铁梅.计量经济分析方法与建模（2版）［M］.北京：清华大学出版社，2009.

［2］樊欢欢，张凌云.Eviews统计分析与应用［M］.北京：机械工业出版社，2009.

［3］杭州统计信息网.2009年杭州统计年鉴 ［EB/OL］.2009-10-15.http://www.hzstats.gov.cn/web/ShowNews.aspx?id= K7TYu2b6ZN4=.

［4］陈伟国，张红伟.金融发展与经济增长——基于1952—2007年中国数据的再检验［J］.当代经济科学，2008，30（3）：49-56，125.

［5］张晓峒.计量经济学软件EViews使用指南（2版）［M］.天津：南开大学出版社，2006.

［6］张晓峒.计量经济分析［M］.北京：经济科学出版社，2000.

［7］孙士金.安徽省金融发展与经济增长：基于VAR和VEC模型的实证［J］.统计教育，2010，（3）：18-27.

［8］张方波.我国产业结构优化调整的相互关系实证研究——基于向量自回归模型（VAR）［J］.商业文化（学术版），2010，（6）：331-332.

Analysis of Three-industry-structure in Hangzhou Based on the VAR and VEC Model

Yang Changzheng
（School of Management,Guilin University of Technology,Guilin 541004，China）

Through literature reviews,the article points out the defect and the limitation of traditional statistic approaches.Considering these problems and characteristic of those econometrics analysis,it puts forward the application of conbination of vector auto regression（VAR）and vector error correction（VEC）to the analysis of three industries，and explains its advantages in the econometrics analysis, and introduces its theory,then shows its modeling steps through exemplification.Through the data analysis of three industries of Hangzhou city from 1978 to 2008,it comes to conclusion that the analysis is in accordance with its facts,so the method is constructive and can be used in the practice.

industrial industries;vector auto regression;correction model;empirical study

2011-05-09

阳长征（1984-），男，广西百色人，桂林理工大学，硕士研究生；研究方向：战略管理。

F211

A

（责任编辑 张九庆）