F-G广义凸函数与半连续函数

黄金莹，赵 宇，李 东，刘秀娟

（佳木斯大学理学院，黑龙江佳木斯 154007）

F-G广义凸函数与半连续函数

黄金莹，赵 宇，李 东，刘秀娟

（佳木斯大学理学院，黑龙江佳木斯 154007）

文章研究了F-G广义凸函数，并利用条件P1、P2所蕴含的等式关系，得到两个稠密性定理，进而得到两个与半连续性相关的F-G广义凸函数的充分条件，最后将结果应用于不同类型的广义凸函数.

F-G广义凸函数；中间点F-G广义凸函数；条件P1；条件P2

凸性及广义凸性是不等式研究的主要内容，同时也在最优化理论方面起着重要作用.目前文献中出现了不同类型的广义凸函数，大致可以分成两类：一类是以不等式的创建和改进为目的，通过将凸函数进行映射变换所构造的广义凸函数，包括几何凸函数［1－2］、rP-凸函数［3］等；另一类则是以讨论极值问题最优性条件为目的，通过将凸性条件弱化所构造的广义凸函数，如不变凸函数［4－6］、预不变拟凸函数［7］等.

文献［8］给出了严格F-G广义凸函数，并给出了条件P1、P2及其性质，对严格F-G广义凸函数的性质和两个充分条件进行了研究.该文在此基础上，进一步抽象出各类具体广义凸函数的本质特征，得到两个与半连续性相关的F-G广义凸函数的充分条件.

1 定义及引理

文献［8］给出如下定义：

定义1［8］称集合K⊂Rn是关于F的广义凸集，若存在向量值函数F：K×K×［0，1］→Rn，使得∀λ∈［0，1］，∀x，y∈K，有F（x，y，λ）∈K.

将上述中K⊂Rn换成D⊂R，就会有：称集合D⊂R是关于G的广义凸集，若存在数量函数G：D×D×［0，1］→R，使得∀λ∈［0，1］，∀s，t∈D，有G（s，t，λ）∈D.

定义2［8］设K⊂Rn是关于F的广义凸集，D⊂R是关于G的广义凸集，称数量函数f：K→D在K上是F-G广义凸函数，若∀λ∈［0，1］，∀x，y∈K，有f［F（x，y，λ）］≤G［f（x），f（y），λ］.

下文始终用K表示Rn中的点集，用D表示R中的点集，而用F表示K×K×［0，1］→Rn的向量值函数，用G表示D×D×［0，1］→R的数量函数.

定义3［8］设K⊂Rn是关于F的广义凸集，称F在K上满足条件P1、P2，若∀α，β∈［0，1］，且α＜

β∀xy∈K有

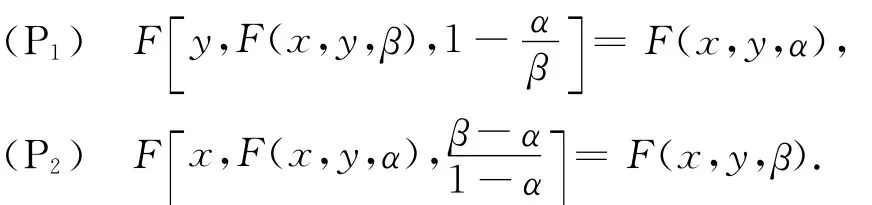
同样可以定义G满足条件P1、P2的概念.

为叙述方便，再给出如下定义：

定义4 称G在D上是正规的，若G在D上满足条件P1且关于λ在［0，1］连续，G（s，t，λ）关于s，t在D上非减，即∀λ∈［0，1］，∀s1，s2，t1，t2∈D，有G（s1，t1，λ）≤G（s2，t2，λ）.

定义5 设K⊂Rn是关于F的广义凸集，D⊂R是关于G的广义凸集，称数量函数f：K→D在K上是中间点F-G广义凸函数，若∃α∈（0，1），∀x，y∈K，f［F（x，y，α）］≤G［f（x），f（y），α］.

称数量函数f：K→D在K上是端点F-G广义凸函数，若∀x，y∈K，有f［F（x，y，0）］≤G［f（x），f（y），0］，f［F（x，y，1）］≤G［f（x），f（y），1］.

对于条件P1、P2，文献［8］给出了定理1和定理3，该文给出如下引理：

引理1［8］若F在K上满足条件P1，则对∀λ∈（0，1），∀u1，u2∈［0，1］，u1＞u2，∀x，y∈K，有F（x，y，λu1＋（1－λ）u2）＝F［F（x，y，u1），F（x，y，u2），λ］.

其证明见文献［8］定理1的证明过程ii），该文从略.

引理1中F换成G在关于G的广义凸集D⊂R中考虑也同样成立.

引理2［8］若向量函数η：Rn×Rn→Rn在K上满足条件C，则F（x，y，λ）＝y＋λη（x，y）在K上满足条件P1、P2.

其证明见文献［8］定理3的证明，该文从略.

2 稠密性定理

定理1（稠密性定理） 设F在K上满足条件P1，G在D上是正规的，f：K→D在K上关于F-G既是中间点广义凸函数也是端点广义凸函数，则集合A＝｛λ｜λ∈［0，1］，∀x，y∈K，f［F（x，y，λ）］≤G［f（x），f（y），λ］｝在［0，1］稠密.

证明 因f在K上关于F-G既是中间点广义凸函数也是端点广义凸函数，故∃α，0，1∈A，其中α∈（0，1）.

假设A在［0，1］非稠，则存在λ0∈（0，1），对λ1＝inf｛λ∈A｜λ≥λ0｝，λ2＝sup｛λ∈A｜λ≤λ0｝，有0≤λ2＜λ1≤1.

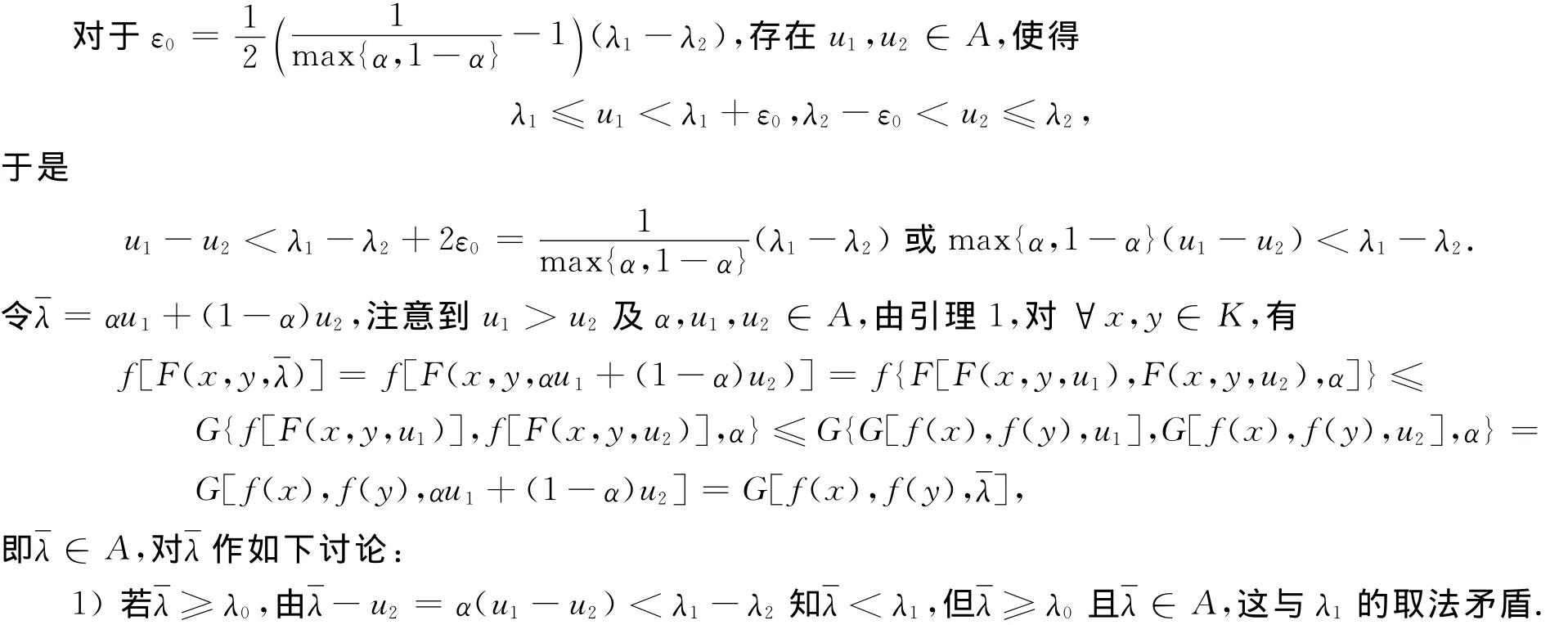
综上，假设不成立，故A在［0，1］中稠密.

受文献［9］定理6的启发，改变定理1中f为中间点广义凸函数的条件，可以得到一个与下半连续相结合的稠密性定理：

定理2 设F满足条件P1且关于λ在［0，1］连续，G在D上是正规的，f：K→D在K上是下半连续函数且是端点F-G广义凸函数，又∀x，y∈K，∃α∈（0，1），有f［F（x，y，α）］≤G［f（x），f（y），α］，则集合A＝｛λ｜λ∈［0，1］，∀x，y∈K，f［F（x，y，∀x，yλ）］≤G［f（x），f（y），λ］｝在［0，1］稠密.

证明 因f在K上关于F-G是端点广义凸函数，故0，1∈A.

假设A在［0，1］非稠，则存在λ0∈（0，1），对λ1＝inf｛λ∈A｜λ≥λ0｝，λ2＝sup｛λ∈A｜λ≤λ0｝，有0≤λ2＜λ1≤1.

根据确界性质，∃βn∈A，βn≤λ2，βn→λ2，因为F关于λ在［0，1］连续，就有

因f在K上是下半连续函数，故对∀ε＞0，∃N∈N＋，∀n＞N，有

根据定理2可以获得下半连续前提下F-G广义凸函数的充分条件.

定理3 设F满足条件P1且关于λ在［0，1］连续，G在D上是正规的，f：K→D在K上是下半连续函数且是端点F-G广义凸函数，又有∀x，y∈K，∃α∈（0，1），f［F（x，y，α）］≤G［f（x），f（y），α］，则f在K上是F-G广义凸函数.

证明 因为f在K上是端点F-G广义凸函数，故只需证∀λ∈（0，1），∀x，y∈K，有

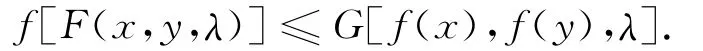
由定理2知，集合A＝｛λ｜λ∈［0，1］，∀x，y∈K，f［F（x，y，λ）］≤G［f（x），f（y），λ］｝在［0，1］稠密.于是对∀λ∈（0，1），∃λn∈A，λn→λ，因为F关于λ在［0，1］连续，就有

因f在K上是下半连续函数，所以对∀ε＞0，∃N∈N＋，∀n＞N，有

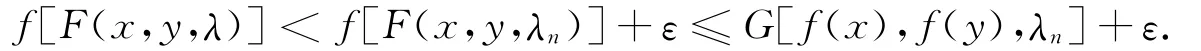
注意到G在D上的正规性及ε的任意性，就有

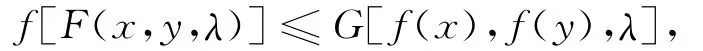
即f在K上是F-G广义凸函数.

根据定理1可以获得如下上半连续前提下F-G广义凸函数的充分条件.

定理4 设F、G满足条件P1、P2且关于λ在［0，1］连续，且G（s，t，λ）关于s，t在D上连续非减，fK→D在K上是上半连续函数且关于F-G既是中间点广义凸函数也是端点广义凸函数，则f在K上是F-G广义凸函数.

证明 由定理1知，集合A＝｛λ｜λ∈［0，1］，∀x，y∈K，f［F（x，y，λ）］≤G［f（x），f（y），λ］｝在［0，1］稠密.任取λ∈（0，1），任取x，y∈K，存在λn∈A，有λn→λ（n→∞）.

可对λn作如下限制：λn∈（0，1），λn＜λ，从而

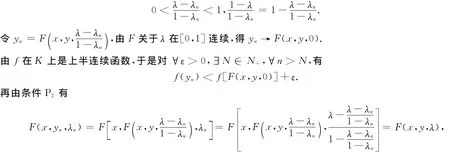
即F（x，yn，λn）＝F（x，y，λ）.

由λn∈A及G（s，t，λ）关于s，t在D上连续非减且f是端点广义凸函数，就有

注意到ε的任意性及G满足条件P2，就有

即f在K上是F-G广义凸函数.

3 主要应用

限于篇幅，以下仅以预不变拟凸函数、几何凸函数这两类广义凸函数为例，且仅验证它们满足定理1条件，对于预不变凸函数、rP-凸函数等同理可以验证.

定理5 设集合K是关η：Rn×Rn→Rn的不变凸集，

i）若函数f：K→R是预不变拟凸函数，则f在K上是F-G广义凸函数；

i）因K是关于η：Rn×Rn→Rn的不变凸集，即∀λ∈［0，1］，∀x，y∈K，有y＋λη（x，y）∈K，F（x，y，λ）∈K，故K是关于F的广义凸集.

∀λ∈［0，1］，∀s，t∈R，有max｛s，t｝∈R，即G（s，t，λ）∈R，故R是关于G的广义凸集.若函数f：K→R是预不变拟凸函数，即

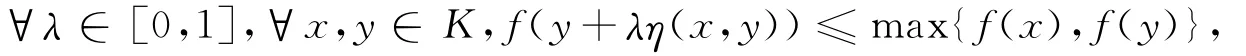
则

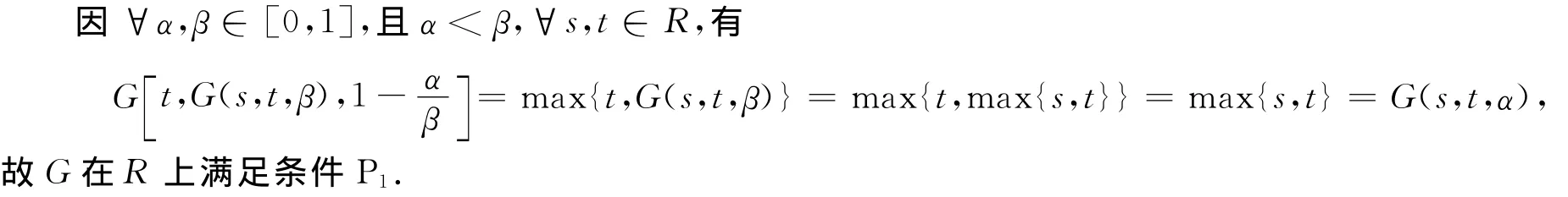
此外，显然G（s，t，λ）关于s，t在R上非减.

综上，验证了定理1诸条件，结论ii）成立.

下面定理需要明确这样的记号：

设Rn＋＋是分量为正的n维实数组全体，对于

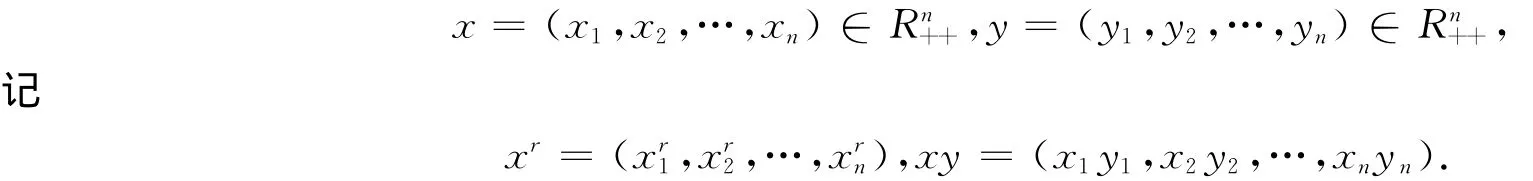
定理6 设集合K⊂Rn＋＋是几何凸集，

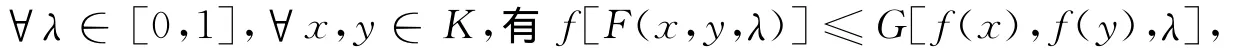
故预不变拟凸函数是F-G广义凸函数.

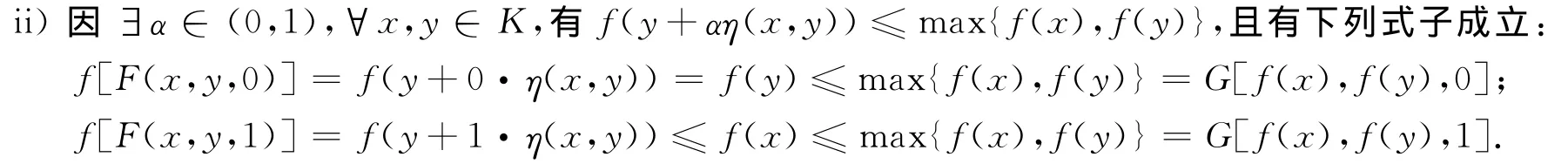
故f在K上关于F-G既是中间点广义凸函数也是端点广义凸函数.

根据引理2及η在K上满足条件C知，F（x，y，λ）＝y＋λη（x，y）在K上满足条件P1.

一些具体广义凸函数的性质及在优化问题中的应用散见于各种文献，将各类广义凸函数抽象为F-G广义凸函数开展一般性研究，是一个宏观化、系统化过程.透过现象探索问题产生的本质根源，将各类广义凸函数作为其特例，不仅解决目前各类广义凸函数的重复研究现象，同时也把一些广义凸函数纳入到优化问题的应用范畴中来，从而丰富了广义凸理论内容，统一了应用于优化问题研究和不等式研究领域的各类广义凸函数，初步构建了广义凸理论体系.

［1］张小明.几何凸函数［M］.合肥：安徽大学出版社，2004.

［2］吴善和.几何凸函数与琴生型不等式［J］.数学的实践与认识，2004，34（2）：155-163.

［3］吴善和.rp－凸函数与琴生型不等式［J］.数学的实践与认识，2005，35（3）：220-227.

［4］Wer T，Mond B.Pre-invex functions in multiple objective optimization［J］.J Math Anal Appl，1988，136（1）：29-38.

［5］Tang Wanmei，Yang Xinmin.The sufficiency and necessity condtions of strongly preinvex functions［J］.OR Transactions，2006，10（3）：50-58.

［6］黄金莹，赵宇，宋丽艳.预不变凸函数的若干性质［J］.哈尔滨师范大学自然科学学报，2009，25（3）：36-39.

［7］Tang Wanmei，Liu qian，Yang Xinmin.The sufficiency and necessity condtions of strongly prequasi-invex functions［J］.OR Transactions，2007，11（3）：21-30.

［8］赵宇，黄金莹，刘春妍.严格F-G广义凸函数［J］.杭州师范大学学报：自然科学版，2011，10（1）：20-26.

［9］颜丽佳，刘芙萍.强预不变凸函数［J］.重庆师范大学学报：自然科学版，2005，22（1）：11-15.

［10］Mohan S R，Neogy S K.On invex set and preinvex functions［J］.J Math Anal Appl，1995，189：901-908.

F-GGeneralized Convex Functions and Semicontinuous Functions

HUANG Jin-ying，ZHAO Yu，LI Dong，LIU Xiu-juan

（Department of mathematics，Jiamusi University，Jiamusi 154007，China）

The paper studiedF-Ggeneralized convex functions，obtained two density theorems and two sufficient conditions ofF-Ggeneralized convex functions with respect to semicontinuity of functions by using the equality relation in condition P1and P2，and put these results on some different types of generalized convex functions.

F-Ggeneralized convex functions；intermediate-pointF-Ggeneralized convex functions；condition P1；condition P2

O174.13 MSC2010：90C25；26B25

A

1674-232X（2011）03-0223-05

10.3969／j.issn.1674-232X.2011.03.007

2010-09-09

黑龙江省教育厅科学技术研究资助项目（11551499）.

黄金莹（1973—），男，黑龙江佳木斯人，副教授，硕士，主要从事凸分析与凸规划研究.E-mail：hjyshuxue＠163.com