自旋1／2粒子的Anandan量子相位

王 龙，李 康

（杭州师范大学理学院，浙江杭州 310036）

自旋1／2粒子的Anandan量子相位

王 龙，李 康

（杭州师范大学理学院，浙江杭州 310036）

通过求解狄拉克方程，得出了一个自旋为1／2且具有永久磁偶极矩和电偶极矩的中性粒子在通过电磁场时波函数在非对易空间和非对易相空间的相位变化，并讨论了与之相关的AC效应和HMW效应.

自旋1／2粒子；非对易空间；非对易相空间；Bopp's变换；Anandan相位

近年来，越来越多的人开始关注非对易空间上的物理效应.这是因为不仅在具有背景场的D膜理论低能效应中，而且在弦的尺度下，非对易空间效应问题的研究都具有重大意义.它可能给人们带来时间和空间观念的量子革命.通常研究非对易空间问题的理论主要是非对易量子场论.

对于自旋为1／2的粒子在非对易空间和非对易相空间的AC效应和HMW效应，此前已有很多物理学家做了研究［1－11］，但对于自旋为1／2粒子的Anandan效应，现在的研究很少涉及到，该文在这方面做了一些有用的探究.在非对易空间和非对易相空间中，笔者将重点利用Bopp变换求解自旋为1／2粒子的包含Anandan效应的狄拉克方程，得到一个Anandan相位，并由此出发得到HMW相位和AC相位.

1 对易时空Anandan效应的描述

在对易时空中，坐标和动量满足下列关系：

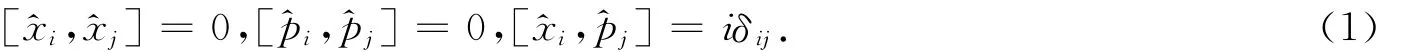
在2＋1维对易时空中，一个具有固有电矩和固有磁矩且自旋为1／2的中性粒子在电磁场中运动时，它的拉氏量具有如下形式：

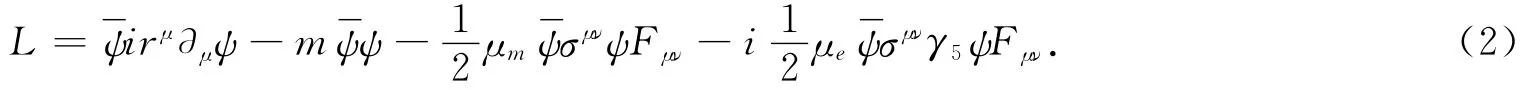
式中后两项分别是粒子的磁矩和电矩与电磁场的相互作用项.又因为σμνγ5＝（i／2）∈μναβσαβ，所以拉式量变为下列形式：

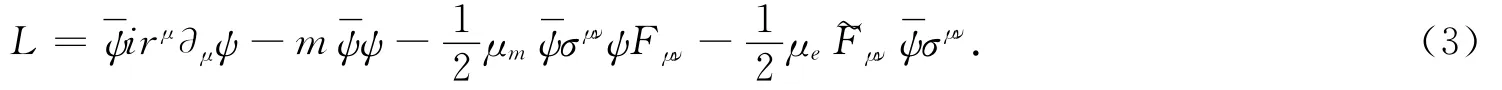
笔者在此用了3个4×4矩阵来描述自旋向上及向下投影在z方向分量.在2＋1维空间，这些矩阵满足下列关系式：

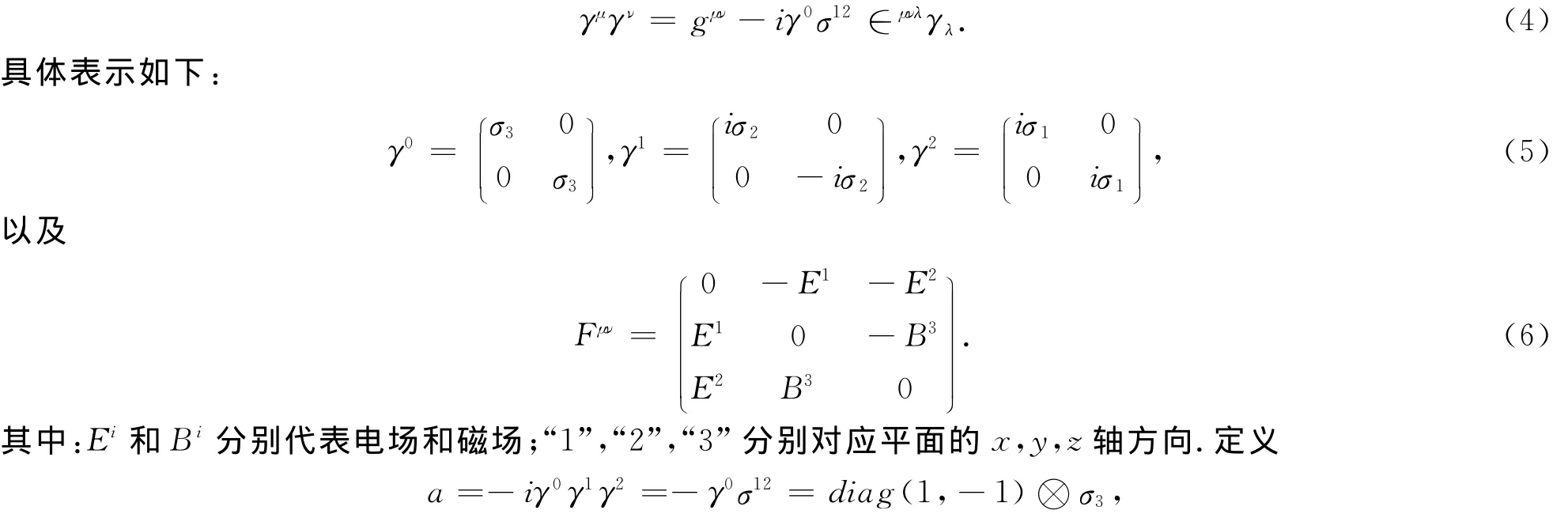
代入式（3）可得

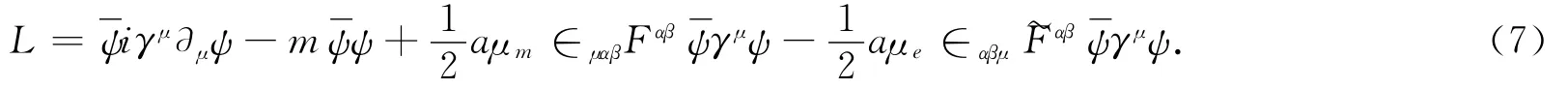
由欧拉—拉格朗日方程可以推出粒子的运动方程为

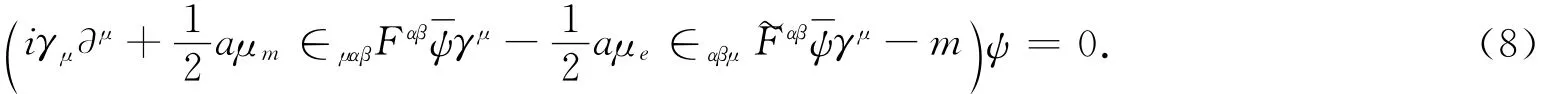
上式可以化简为

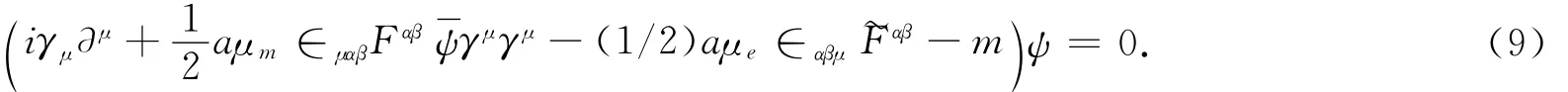
把式（9）的解写成如下形式：

其中ψ0是无电磁场外作用时的解.

则相位φ具有如下形式：

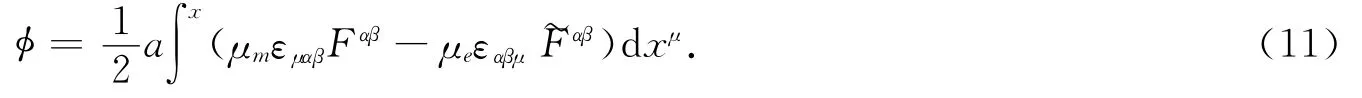
如果考虑一种特殊情形，即粒子在平面运动且处在一根均匀的、无限长的细导线产生的电磁场中，则

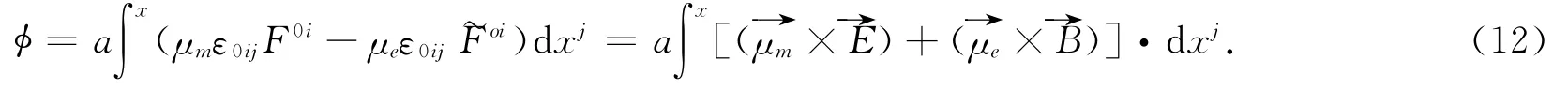
当中性粒子的电矩μe＝0时，可得到AC效应的几何相：

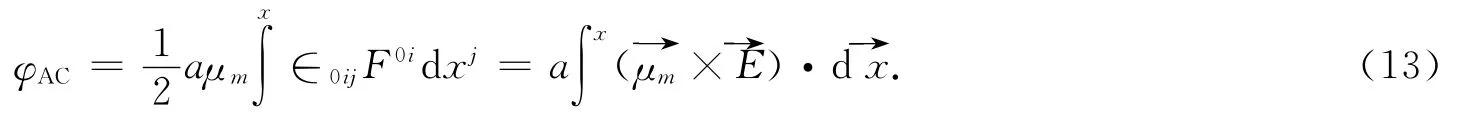
当中性粒子的磁矩为μm＝0时，可得到HMW效应的几何相：

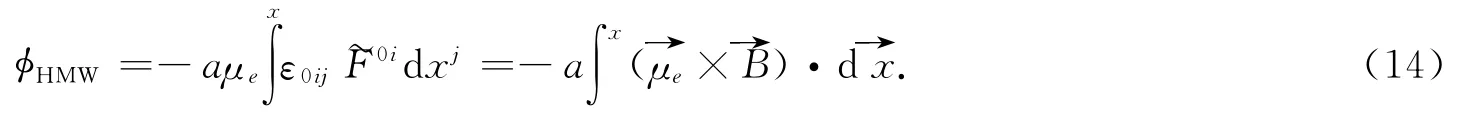
2 非对易空间的Anandan效应

非对易空间下，坐标和动量算符满足下列对易关系：

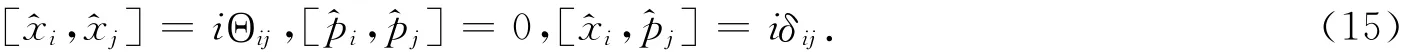
式中：Θij是一个反对称矩阵元素，它的值很小且与能标有关，代表了空间的非对性；x＾i，p＾j是非对易空间的坐标和动量算符.对易空间的量子力学方程只需将普通乘积改为星号（＊）乘积就可转变为非对易空间的量子力学方程［9］，所以在非对空间中，自旋为1／2的且具有固有电矩和磁矩的中性粒子，其狄拉克运动方程可以写为

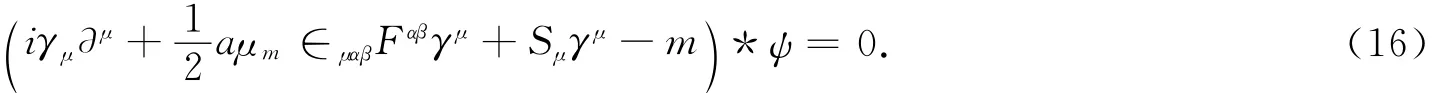
两个任意函数之间的星乘定义如下：

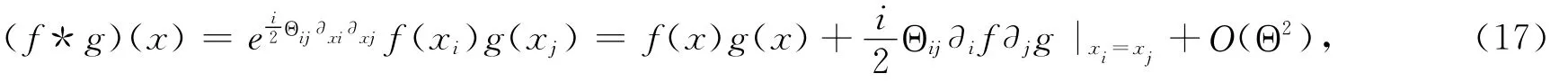
这里的f（x）和g（x）是两个独立的函数.

已有的研究大多是通过直接求解含有星乘运算的运动方程完成的.星乘运算可以用Bopp's变换转换成普通乘法.此时，相应的坐标和动量要做如下变换：

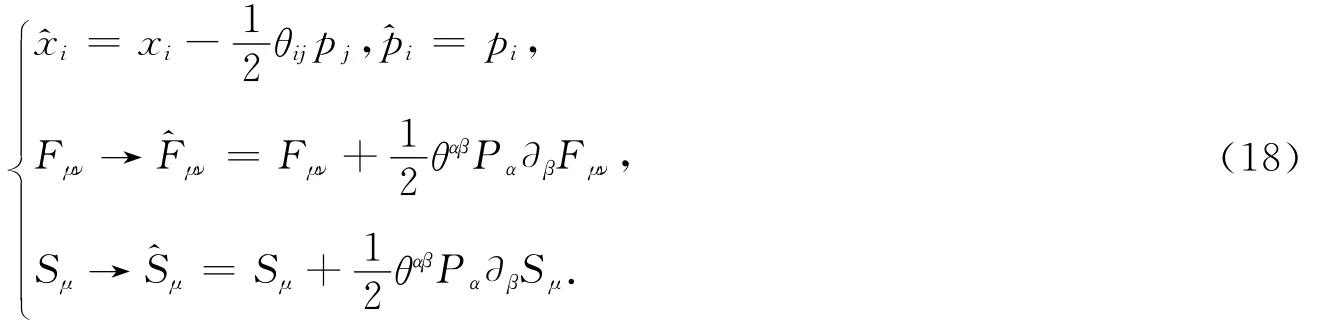
Bopp变换后中性粒子在非对易空间的运动方程为

上述狄拉克方程有如下形式的解：

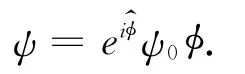
这里ψ0是电磁场无外作用时的解.非对易空间相φ＾具有如下形式：

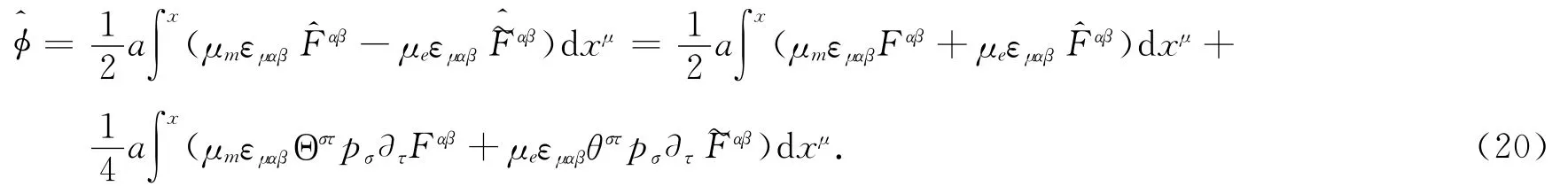
这是自旋为1／2的中性粒子在一般电磁场中的Anandan量子相位.

当中性粒子的电矩μe＝0时，可以得到在非对易空间AC效应的几何相：

当中性粒子的磁矩μm＝0时，可以得到非对易空间HMW效应的几何相：

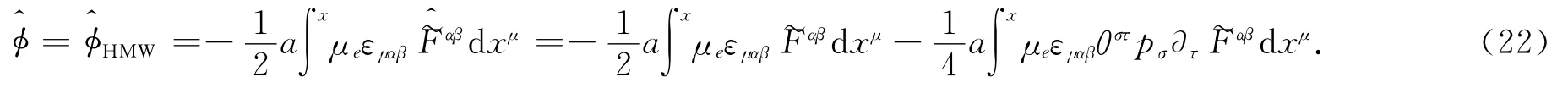
在电磁场存在情况下，粒子在对易空间的哈密顿量具有如下形式：

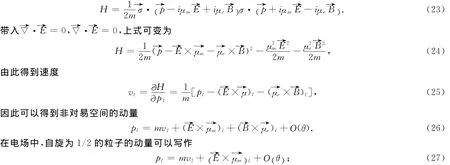
上式的φ为前文讨论过的对易空间的相位，而δφNCS是与非对易空间的相位相联系的.

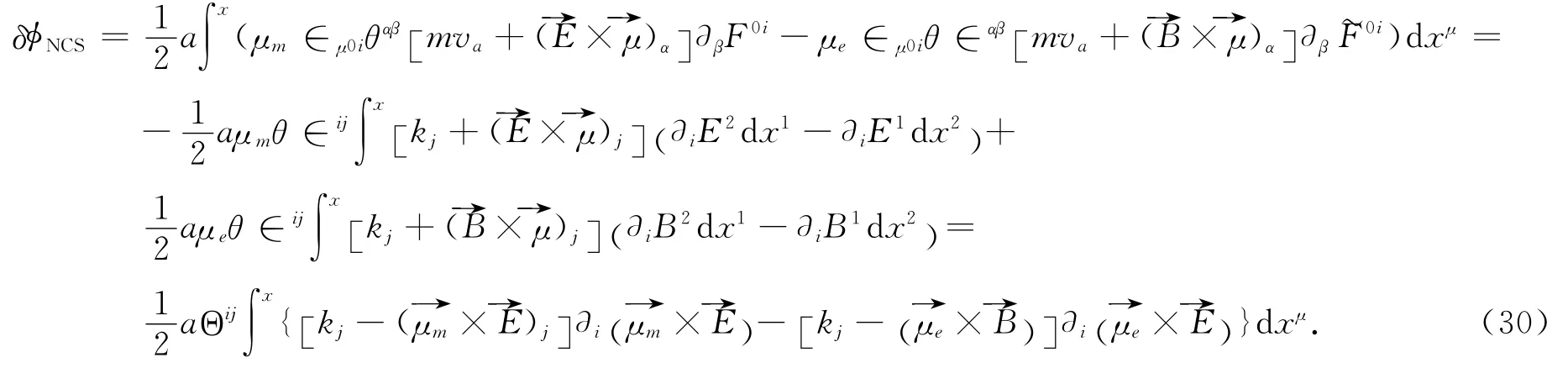
在磁场中，自旋为12的粒子的动量可以写作

式中kj＝mvj.此结果和已有文献［10］星乘法计算结果一致.第一项依赖于速度项的修正，能够修正相位的变换；第二项是对涡流的校正，对线性光谱没有贡献.

3 非对易相空间的Anandan效应

在非对易相空间，坐标和动量算符满足下列对易关系：

类似非对易空间的变换方法，非对易相空间的狄拉克方程变成

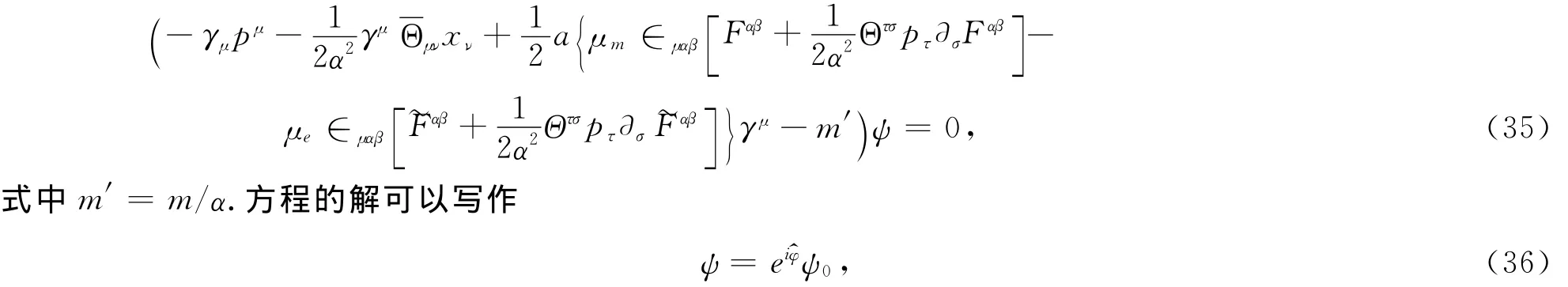
这里ψ0是无电磁场外作用时且质量为m′时的解.φ对应于粒子在非对易空间的相位，它有如下形式：

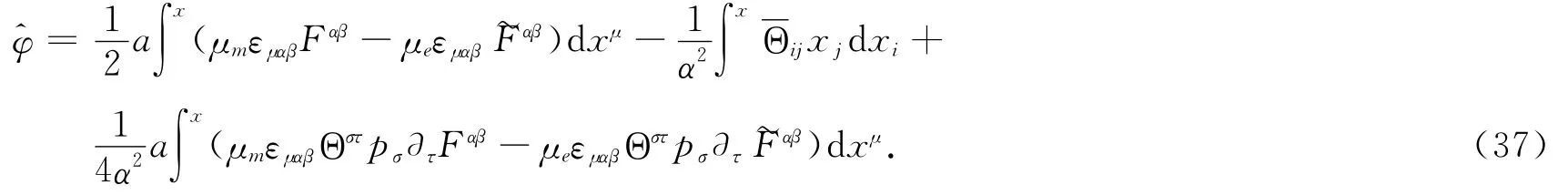
当中性粒子的电矩μe＝0时，可得到AC效应的几何相：

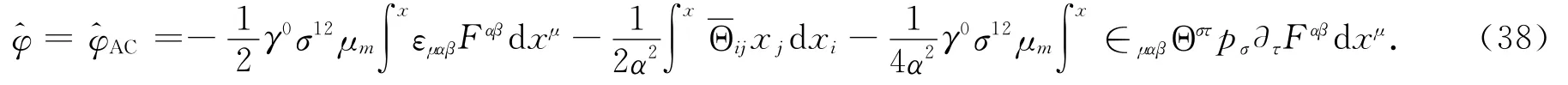
当中性粒子的磁矩μm＝0时，可得到HMW效应的几何相：

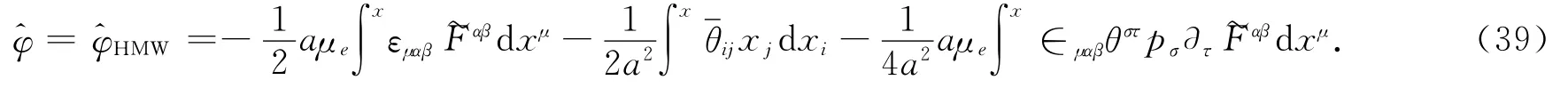
在非对易相空间，粒子在电磁场中运动，Anandan量子相位可以写作

这里φ对应于对易空间的相位，δφNCS对应于非对易空间对相位的贡献，δφNCPS为非对易相空间对相位的贡献.

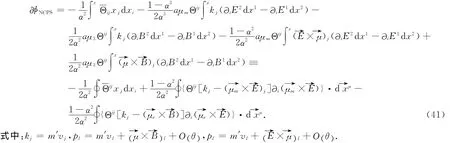
4 结 论

该文研究了非对易空间和非对易相空间的Anandan效应.相对于传统的直接求解含有星乘运算的运动方程的方法，文中采用的是用Bopp's变换把非对易空间和非对易相空间的含有星乘运算的运动方程转变为对易空间的含有普通乘法的运动方程，然后再求出相应的Anandan的量子相位，并且从Anandan的量子相位又推导出了AC效应和HMW效应的相位.这种求解方法使原本复杂的求解过程变得简单明了，它对于解决其它粒子相位问题也具有一定的启示性作用.

［1］Seiberg N，Witten E.String theory and noncommutative geometry［J］.Journal of High Energy Physics，1999（9）：1-99.

［2］Mirza B，Zarei M.Non-commutative quantum mechanics and the Aharonov-Casher effect［J］.Eur Phys J C，2004，32（4）：583-586.

［3］Li Kang，Dula S.The Aharonov-Bohm effect in noncommutative quantum mechanics［J］.Eur Phys J C，2006，46（3）：825-828.

［4］Li Kang，Wang Jianhua，Chen Chiyi.Representation of noncommutative phase space［J］.Mod Phys Lett A，2005，20（28）：2165-2174.

［5］He Xiaogang，McKellar B H J.Topological effects，dipole moments，and the dual current in 2＋1dimensions［J］.Phys Rev A，2001，64（2）：1-6.

［6］Aharonov Y，Casher A.Topological quantum effects for neutral particles［J］.Phys Rev Lett，1984，53（4）：319-321.

［7］Hagen C R.Exact equivalence of spin-1／2Aharonov-Bohm and Aharonov-Casher effects［J］.Phys Rev Lett，64（20）：2347-2349.

［8］Kamani D.Noncommutativity and the motion of Dpbrane along itself［J］.Europhys Lett，2002，57（5）：672-676.

［9］Li Kang，Wang Jianhua.The topological AC effect on non-commutative phase space［J］.Eur Phys J C，2007，50（4）：1007-1011.

［10］Passos E，Ribeiro L R，Furtado C.Noncommutative Anandan quantum phase［J］.Physical Review A，2007，76（1）：1-7.

［11］Wang Jianhua，Li Kang.The HMW effect in noncommutative quantum mechanics［J］.J Phys A，2007，40（9）：1-8.

Anandan Quantum Phase of Spin-1／2Particles

WANG Long，LI Kang

（College of Sciences，Hangzhou Normal University，Hangzhou 310036，China）

By solving the Dirac function，the paper obtained the phase changes of the wave function in non-commutative space and non-commutative phase space when a neutral spin-1／2particle with nonzero magnetic and electric dipoles moved in an external electromagnetic field，and discussed the related Aharonov-Casher effect and the He-McKellar-Wilkens effect.

spin-1／2particle；non-commutative space；non-commutative phase space；Bopp's shift；Anandan p hase

O413.3 MSC2010：81Q99；14M99；53Z05

A

1674-232X（2011）03-0262-05

10.3969／j.issn.1674-232X.2011.03.015

2010-11-16

王 龙（1977—），男，山西临汾人，理论物理专业硕士研究生，主要从事量子场论与量子力学及其前沿相关问题研究.E-mail：386349745＠qq.com