两个初值修正灰色GOM(1,1)模型及其等价性研究
何 霞,刘卫锋
(郑州航空工业管理学院数理系,河南郑州 450015)
两个初值修正灰色GOM(1,1)模型及其等价性研究
何 霞,刘卫锋
(郑州航空工业管理学院数理系,河南郑州 450015)
根据反向累加生成GOM(1,1)模型的初值取x0(1)(1)的情况,提出两个不同初值修正形式x0(1)(1)+β1,β2x0(1)(1),利用原始序列预测值的误差在最小二乘意义下最小准则,得到两个初值修正的优化GOM(1,1)模型,并证明了这两个初值修正GOM(1,1)模型的等价性和极高的模拟精度.
GOM(1,1)模型;灰色系统;初值修正;等价性
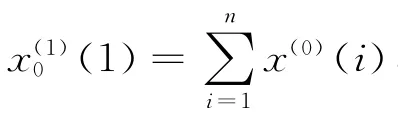
1 反向累加生成及灰色GOM(1,1)模型的建模机理
定义1[1-2]设原始序列为x(0)=(x(0)(1),x(0)(2),…,x(0)(n)),令
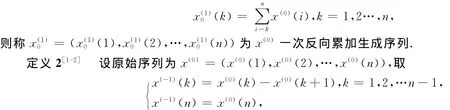

2)灰色GOM(1,1)模型的时间响应序列为

3)原始序列模拟值为
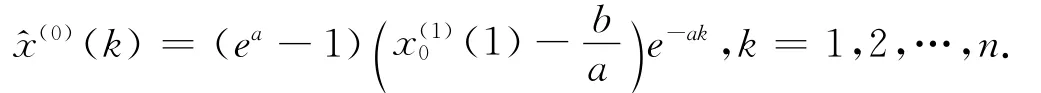
2 两个初值修正的灰色GOM(1,1)模型
2.1 初值修正方法Ⅰ

为使指标函数f取最小值,令
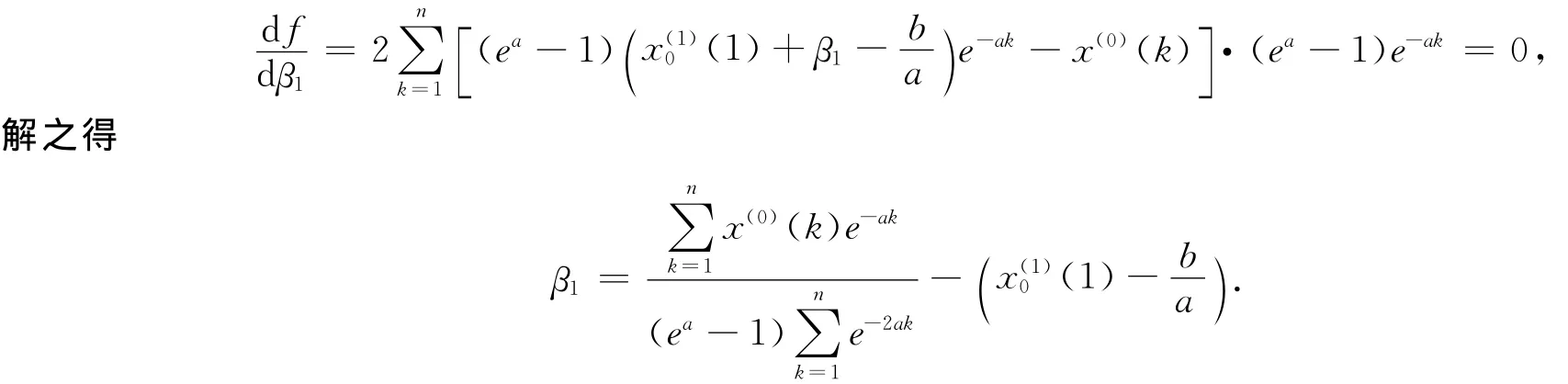
于是得到第一个初值修正的GOM(1,1)模型:
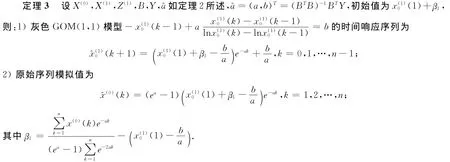
2.2 初值修正方法Ⅱ
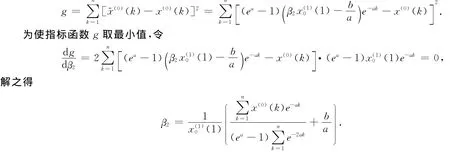
于是得到第二个初值修正的GOM(1,1)模型:
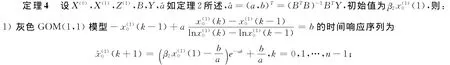
2)原始序列模拟值为
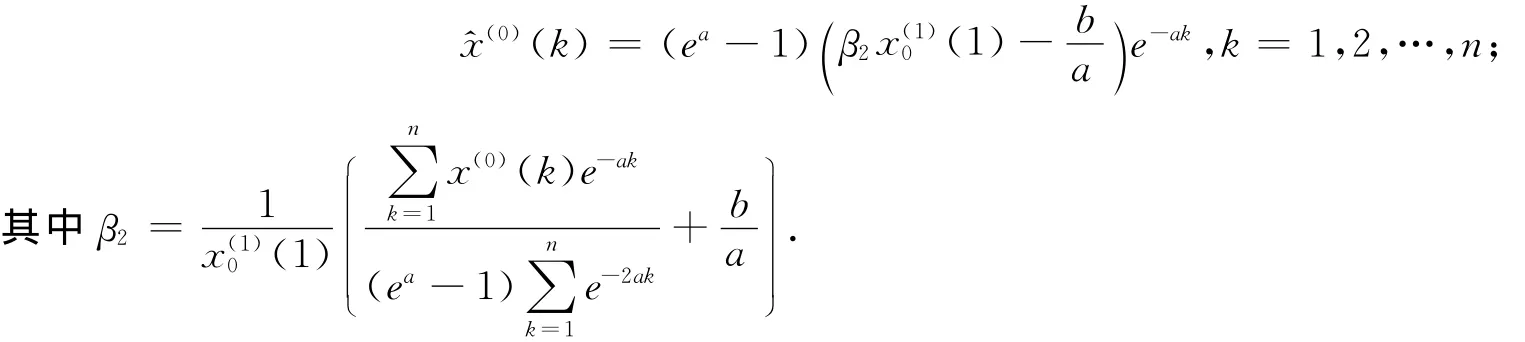
3 两个初值修正灰色GOM(1,1)模型的等价性

4 数据模拟精度比较
为了更好地加以比较,现取文献[4]中例2作为研究对象,通过该文中初值修正方法 Ⅰ 得到灰色GOM(1,1)模型,并与文献[4]中改进的灰色GOM(1,1)模型作比较.

表1 原始序列值Tab.1 The values of original sequence
根据该文初值修正方法Ⅰ建立灰色GOM(1,1)模型:
原始序列为x(0)=(10 000,1 353.35,183.16,24.79,3.35),一次反向累加生成序列为x(1)0=(11 564.65,1 564.65,211.30,28.14,3.35),令
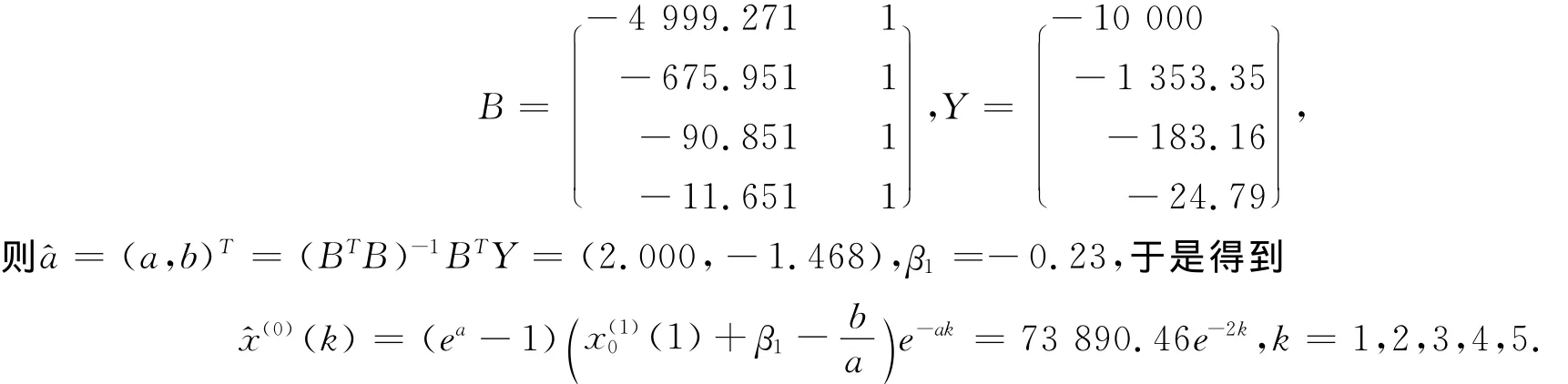
所以,原始数据模拟值为x^(0)=(9 999.99,1 353.35,183.16,24.79,3.35).
文献[4]中的改进灰色GOM(1,1)模型的时间相应式为x^(1)(k+1)=11 565.38e-1.9999997k-0.73.为示区别,将文献[4]中的改进灰色GOM(1,1)模型记为模型1,该文中根据初值修正方法Ⅰ得到的灰色GOM(1,1)模型记为模型2,两模型的模拟精度见表2.
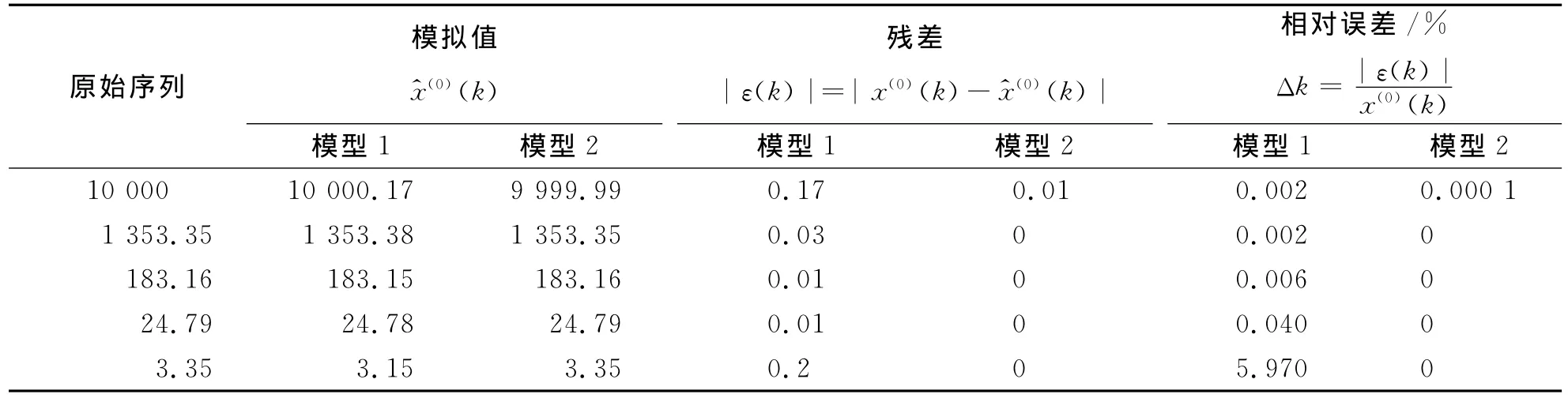
表2 模型1与模型2的模拟精度比较Tab.2 Comparisons between fitting precision of model 1and model 2
由表2可以看出,尽管文献[4]中模型的模拟精度较高,而该文中初值修正为x0(1)(1)+β1的模型的模拟精度更高,同时由模型的等价性可知,初值修正为β2x0(1)(1)的模型具有同样高的模拟精度,因而该文中的初值修正灰色GOM(1,1)模型具有极高的模拟精度,十分适合于高递减速率指数序列建模.
5 结 论
1)该文通过初值修正,利用原始序列预测值的误差在最小二乘意义下最小准则,分别建立了两个优化GOM(1,1)模型,从而拓展了GOM(1,1)模型.
2)该文证明了这两个形式不同的优化GOM(1,1)模型之间存在着本质联系,即它们之间是等价的.
3)经过数据模拟计算实例说明,该文中的两个初值修正GOM(1,1)模型都具有极高的模拟精度,因此也具有极强的实用性.
[1]宋中民,邓聚龙.反向累加生成及灰色GOM(1,1)模型[J].系统工程,2001,19(1):66-69.
[2]宋中民,肖新平.反向累加生成及灰色GOM(1,1)模型[J].武汉理工大学学报:交通科学与工程版,2002,26(4):531-533.
[3]刘金英,杨天行,王淑玲.反向GOM(1,1)模型参数的直接求解方法[J].吉林大学学报:工学版,2003,33(2):75-79.
[4]杨知,任鹏,党耀国.反向累加生成与灰色GOM(1,1)模型的优化[J].系统工程理论与实践,2009,29(8):160-164.
[5]陈鹏宇.GOM(1,1)模型背景值构造的重新改进[J].杭州师范大学学报:自然科学版,2010,9(1):33-36.
[6]张辉,胡适耕.GM(1,1)模型的边值分析[J].华中科技大学学报:自然科学版,2001,29(4):110-111.
Two Grey GOM(1,1)Models Based on Modified Initial Value and Its Equivalence
HE Xia,LIU Wei-feng
(Department of Mathematics and Physics,Zhengzhou Institute of Aeronautical Industry Management,Zhengzhou 450015,China)
Based on the initial value x(1)0(1)of opposite-direction accumulated generating GOM(1,1)model,the paper provided two different modified initial value forms x(1)0(1)+β1,β2x(1)0(1).Using the principle that minimum squares to minimize the errors of new fitting value of original sequence,the paper obtained two optimized GOM(1,1)models,and proved the equivalence as well as the great simulation accuracy of the two optimized GOM(1,1)models.
GOM(1,1)model;grey system;modified initial value;equivalence
O159;C93l MSC2010:93A99
A
1674-232X(2011)03-0217-06
10.3969/j.issn.1674-232X.2011.03.006
2010-11-19
何 霞(1976—),女,河南周口人,讲师,硕士,主要从事灰色系统理论研究.E-mail:hexia@zzia.edu.cn

