路基不均匀沉降对有砟轨道沉降影响的模型试验
邹春华,周顺华,王炳龙,韦 凯
(1.同济大学 道路与交通工程教育部重点实验室,上海201804;2.西南交通大学 牵引动力国家重点实验室,成都610031)
由于线路纵向地基土厚度及土层性质的变化、路堤填料不均匀性、地下水交替作用及基床病害等问题的存在,铁路路基不均匀沉降不可避免[1].路基不均匀沉降一方面使轨道结构产生变形附加应力,可能导致结构性损坏,另一方面可导致其服务性能的下降,从而对行车舒适性和安全性产生影响.现阶段我国铁路正向高速化、重载化的方向发展,铁路在高频、重载作用下除了对轨道结构产生不同形式损坏外,还将进一步引起路基的不均匀沉降,从而加重轨道结构的损坏.
对于有砟轨道下沉变形与高低不平顺发展间的关系国内外已进行了一些研究[2-4],然而这些研究中轨道的下沉变形包括路基沉降,难以明确路基沉降对轨道结构的影响.对于这一问题,目前学术界的侧重点仍多集中在路桥过渡段[5-8],对一般路段的研究较少,且这些研究都主要是针对无砟轨道来开展[9-10].总而言之,对于有砟轨道,由于散体道砟物理力学特性的复杂性[10]以及研究投入力度(或关注侧重点)等方面的原因,截至目前鲜有关于路基不均匀沉降对有砟轨道影响等方面的研究报道问世,但是该类问题研究的理论意义及应用前景都很大,值得深入研究.
为此,通过设计1∶1的室内有砟轨道系统模型试验,采用激振设备近似模拟的列车荷载长期作用,对路基不均匀沉降引起有砟轨道累积变形的发展情况进行了研究,其主要目的是研究在有砟轨道变形稳定后,轨枕空吊现象出现前后路基不均匀沉降与轨道不均匀下沉之间的关系,为路基不均匀沉降对有砟轨道结构影响等方面的进一步研究提供试验与理论支持.
1 模型试验
1.1 试验设计的思路
路基不均匀沉降发展到一定程度,上部轨面也将随之下沉,不可避免地将会影响到轨道不平顺,而轨道不平顺的改变又将加剧轮轨动荷载,使路基不均匀沉降进一步恶化.鉴于此特点,试验以有砟轨道为研究对象,在其底部人为地设计出不同纵向长度与沉降深度的路基不均匀沉降槽,用以研究长期列车动荷载作用下有砟轨道累积变形稳定后路基不均匀沉降与轨道不均匀沉降之间的关系.
需要指出的是,当路基不均匀沉降严重时,轨枕可能出现空吊现象,但是这种现象在现实铁路运营中是很少出现的(因为轨枕空吊对轨道结构及行车的危害极大,而养护部门的重要工作之一就是避免有砟轨道出现这种现象),同时轨枕空吊后路基不均匀沉降与轨面沉降的关系也极其复杂,会受到很多因素的影响,本文对这一问题不作深入研究,重点分析轨枕不空吊时路基与轨道沉降之间的关系.
为此试验前需确定引起轨枕脱空时路基不均匀沉降的临界值,由于该临界值的计算尚无成熟理论,所以采用材料力学理论对轨枕脱空临界值进行粗略的估算,在此基础上设计不同路基不均匀沉降对比工况,重点研究在有砟轨道变形稳定后,轨枕不出现空吊情况下路基不均匀沉降与有砟轨道不均匀沉降的对应关系.
1.2 试验组件的介绍
按照上述思路设计了1∶1有砟轨道系统模型试验,如图1所示.试验中使用60钢轨铺设了12.5 m 长的线路,轨枕用钢筋混凝土Ⅱ型轨枕,扣件为Ⅲ型弹条扣件.道砟级配和断面尺寸符合《京沪高速铁路设计暂行规定》.道床下方是刚性混凝土支承面,其中有一段是使用细砂和PVC(聚氯乙烯)管填充的凹槽,试验中通过抽PVC管实现对余弦型路基不均匀沉降模式的近似模拟.在与轮轴刚性连接的转向架上方放置与之刚连的激振器(SBZ60型变频变矩式振动机),用以近似模拟列车动荷载作用.室内1∶1有砟轨道系统模型试验现场照片如图2所示.需要特别指出的是,由于在1∶1室内不同工况模型试验中保持道砟厚度完全相同的难度非常大,故最终的道砟厚度是以道床捣固整平后的实际厚度为准.试验最后通过轨枕高程的量测,确定道砟振捣完成后的厚度分别为:第1组43.6cm、第2组43.0cm、第3组45.6cm,道床厚度的变化并不大.
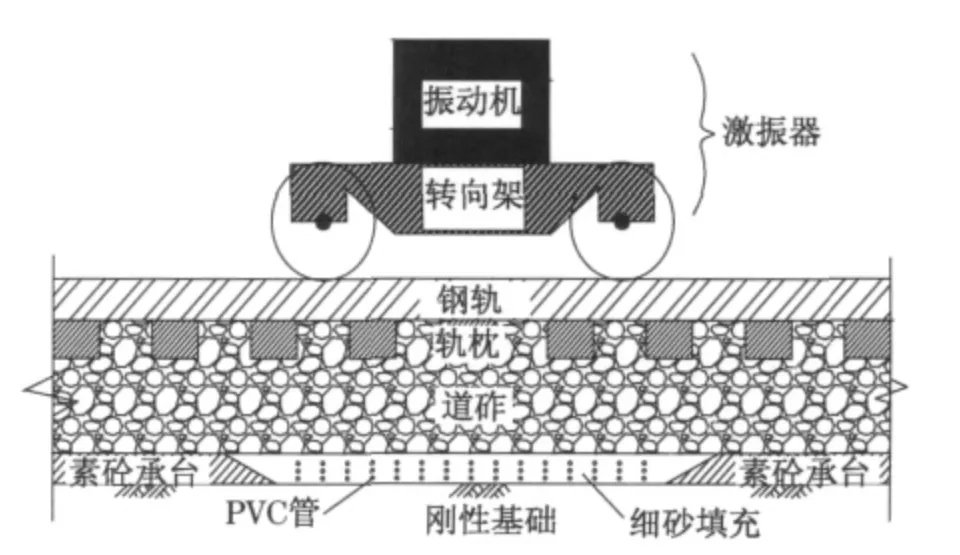
图1 1∶1轨道模型试验系统示意图Fig.1 Sketch map of 1∶1track model test

图2 1∶1轨道模型试验系统照片Fig.2 Photograph of 1∶1track model test
1.3 荷载模拟
(1)有砟轨道列车荷载
有砟轨道结构的累积沉降变形主要由列车动荷载作用引起,考虑相邻两节车厢的转向架间距一般为4~8m,转向架轴距2.5m,同一车厢的两个转向架之间的距离一般是10~18m,车辆的运行速度一般为80~300km·h-1(甬台温有砟轨道铁路最高时速达292km·h-1),那么动荷载频率的变化范围在1.2~33.3Hz之间;考虑客运与货运两种情况,列车的轴重变化较大,一般在12~25t之间.
(2)实验室列车荷载的模拟
实际工程中列车荷载的大小与频率变化范围较大,本文仅研究位于该范围内的某一确定轴重与频率的情况.在试验仪器调试过程中发现当荷载增大到一定值时,动荷载会引起实验室自身及周边建筑物的强烈振动.为确保试验安全顺利的进行,确定采用频率13.1Hz的6.85~11.05t的循环动荷载.然而,在试验实施过程中,由于每组试验道床的厚度的差异,引起振动能量传递、衰减与放大情况变化很大,使每组试验周边环境的振动响应不同.因此,对荷载激振力的大小及频率做了微调,最终确定3 组试验的动荷载频率分别为14.2、13.1和12.25 Hz,对应模拟一个转向架情况下列车轴重最小与最大值为6.55~11.45t、6.85~11.05t和7.2~10.8t.有研究[11]指出荷载频率对颗粒材料的长期累积变形影响可忽略,而本试验中荷载频率变化较小,因此荷载频率微小变化的影响在试验中不予考虑.与此同时,国内外实测与室内试验结果都表明,列车轴重与有砟轨道的长期累积变形成线性关系,因此试验所模拟荷载的大小变化将对试验结果产生影响.尽管如此,但是由于试验荷载大小的调整量相对于试验荷载的总大小来说是非常小(仅为其3.6%),可认为模拟荷载大小的微小调整对本试验结果的影响甚小.
1.4 路基不均匀沉降模拟设计
(1)轨枕临界脱空情况下路基不均匀沉降估算
为了估算出有砟道床轨枕临界空吊情况下路基不均匀沉降槽的临界面积值,首先作了如下3点基本假定:①路基不均匀沉降槽假定为余弦型沉降槽;②假定路基不均匀沉降在道砟中的传播角度为道砟的自然休止角,试验中测得道砟的自然休止角为42°,在未出现轨枕空吊前钢轨与道砟沉降槽的面积相等S2=S3(如图3所示),由此可估算出路基不均匀沉降槽传递到钢轨面的影响范围;③钢轨与轨枕作为一个整体被看作简支梁,通过计算试验静荷载作用下其挠度的大小,即可估算出该最大挠度对应的轨面沉降槽面积,从面得到引起轨枕空吊的路基不均匀沉降槽临界面积值.

图3 路基沉降与轨道沉降示意图Fig.3 Sketch map of subgrade settlement and track settlement
基于以上假定,利用材料力学简支梁计算公式(见式(1))可得到有砟道床轨枕空吊情况的路基不均匀沉降槽临界面积值.试验中,轮轴+转向架+激振器自重18t、道砟厚度0.4m、路基不均匀沉降宽度在2~3m 内变化.

式中:v为梁的挠度,m;P为集中荷载,N;EI为抗弯刚度,N·m2;l为梁的长度,m;x为离起点的距离,m.
(2)路基不均匀沉降的确定
根据试验目的要求,设计了3组试验,分别研究了轨枕出现临界空吊、轨枕不出现空吊及轨枕完全空吊3种情况下,路基不均匀沉降与轨道不均匀沉降变形的关系.由于试验条件限制,有砟轨道线路全长仅为12.5m,路基不均匀沉降槽宽度不能选取过长,当然也不能选取过短,否则会导致试验结果过小以至于难以辨别其不同工况间的差异.鉴于此本试验计划选取2.5、2.0和3m 的3组试验长度.然而由于试验过程中,模拟的路基不均匀沉降槽宽度与深度较小时,用于模拟路基沉降的PVC 管径与数量变小变稀,导致实际模拟路基沉降槽宽度有波动,3组试验中实际路基沉降槽宽度分别为2.43、2.25、3.00m,据此利用式(1)估算的3组试验临界空吊路基沉降槽临界深度,各自设计了3个试验工况(共9个试验工况),见表1,表中工况一代表每组试验中第1种情况的路基不均匀沉降,它由抽掉第1层PVC管所产生的空隙来模拟;工况二代表每组试验中第2种情况的路基不均匀沉降,它是由抽掉的第1层和第2层PVC管产生的空隙的总和来模拟;工况三代表每组试验中第3种情况的路基不均匀沉降,它是由抽掉的第1层、第2层和第3层PVC 管产生的空隙的总和来模拟.
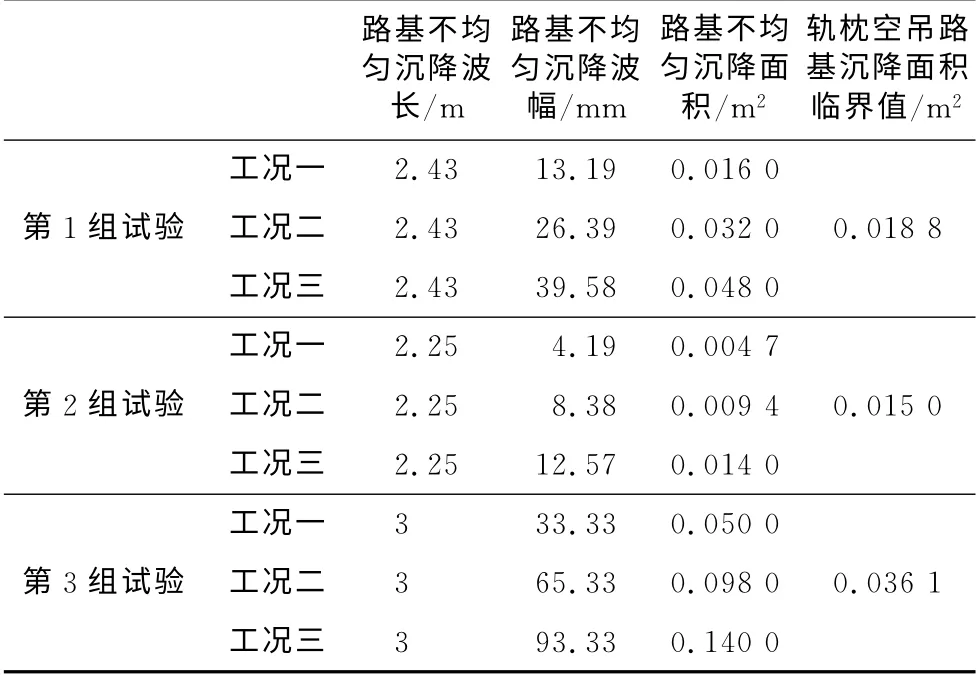
表1 路基不均匀沉降槽参数Tab.1 Parameters of subgrade differential setting tank
(3)路基不均匀沉降的模拟
试验实施过程中采用抽掉PVC 管的体积来模拟给定的路基不均匀沉降槽的大小,为保证PVC 管有足够的刚度,在PVC管中灌充砂粒并振动使其充分密实;为不使PVC 管中的砂粒在试验中松散挤出,在PVC管的两头采用素混凝土封口;同时为保证拔管时不对道砟产生拖带作用,在预留模拟不均匀沉降的空隙顶面铺一层土工布.第1组全部采用外径32mm 与20mm 两种管径的PVC管进行不均匀沉降沉降槽体积的模拟,每根PVC 管的竖向净间隔为10mm,水平向净间隔为37 mm,纵向总长为2.43m,横向长为6m;第2组全部采用外径20mm的PVC管,每根PVC管的竖向净间隔为20mm,水平向中心间隔为150mm,纵向总长为2.25m,横向长为6m;第3组试验,由于模拟的路基不均匀沉降槽体积较大,为使沉降槽的形状更接近于余弦形式,采用了3种不同外径的PVC 管,详见图4所示,每根PVC管的竖向净间隔为10mm,水平向净间隔为10mm,纵向总长为3m,横向长为6m.最终本试验模拟的3组试验余弦型路基不均匀沉降的波长、波幅及对应的不均匀沉降面积见表1.

图4 第3组试验模拟不均匀沉降PVC管布置图(单位:mm)Fig.4 Arrangement diagram of PVC pipe used to imitate the differential settlement in the third group(unit:mm)
1.5 测点布置及量测
轨道结构沉降的量测采用在轨枕面上布测点来实现.轨枕的沉降采用DSZ2精密水准仪进行量测,测点布置与编号如图5所示.图中,Gij表示轨枕测点编号.
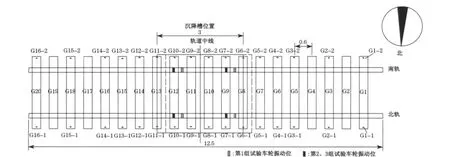
图5 3组试验测点编号(单位:m)Fig.5 Measuring point number of the three groups’test(unit:m)
本文主要研究在路基不均匀沉降作用下,路基不均匀沉降与有砟轨道最终累积沉降变形的关系,因此试验轨道沉降应取轨道沉降变形稳定后的数据进行分析.为得到轨道沉降变形稳定后的数据,试验前先对路基不均匀沉降引起轨道沉降变形的发展随时间、振次的变化进行了观测,结果如图6所示,图中沉降量坐标中正表示降起,负表示沉降.从图中可知振动6 万次后轨道沉降变形的变化趋于稳定值(个别点有跳跃),为更准确地得到轨道沉降变形稳定后的数据,本试验取振动10 万次后沉降变形数据进行分析,并认为此时沉降变形完全稳定.因此,本试验数据均为激振器振动10万次后量测的,即在模拟路基不均匀沉降之前先对轨道各段面进行预振.各断面预振完成后,测轨道高程作为本试验的轨道高程初始值,然后在每个试验工况中都量测振动10万次后的轨道高程,高程差即为轨道的沉降变形.

图6 测点沉降量与荷载作用次数的关系Fig.6 Relationship between the measuring point settlement and the loading number
在测量钢轨面的沉降变形时,激振器无法移开,试验所测轨面沉降变形为有激振器静载作用下的轨面沉降变形,而激振器静荷载的作用可能对试验结果产生一定的影响,但是通过计算分析发现静载作用下轨道沉降的最大值仅为0.107mm,而本试验高程测量的精度为0.1mm,因此可认为静载作用对试验结果的影响很小.
2 试验结果
2.1 余弦型路基不均匀沉降发生后轨面沉降模式
取第1组试验第1种工况下沉降曲线范围的沉降观测数据进行分析,采用余弦型和多项式两种函数对其进行拟合,所得拟合曲线如图7所示.
由图7知,两种函数的拟合相关性都较好,相关系数在0.97以上,但余弦型函数拟合能更好地反映原有数据沉降峰值的大小,而轨道沉降峰值的大小是本文所研究的重点内容之一,此外,余弦型函数所需确定的参数比4次多项式要少,便于实际工程的应用.对3组试验任一工况的沉降数据采用以上两类函数进行拟合分析,得与前面分析结果一致的结论.因此,钢轨的沉降模式均采用余弦型表示.本文随后轨面沉降曲线围成的面积的计算就是按照余弦函数所围成的面积计算公式进行计算的.

图7 沉降曲线的拟合Fig.7 Fitting of settlement curve
2.2 余弦型路基不均匀沉降发生后轨面沉降规律
分别对路基不均匀沉降引起的轨面沉降数据进行分析,第1组试验3个工况路基不均匀沉降槽面积大小的增量是相同的,但轨道的沉降槽面积主要由路基沉降的第1个工况引起,随着路基不均匀沉降槽面积的等量增加轨道的沉降槽面积增量减小,如图8a所示.3个工况情况下路基沉降曲线面积与轨道沉降曲线面积之比分别为1.000、0.719、0.521(见表2),说明第1组试验路基沉降量较小时(第1个工况)路基沉降槽面积与轨道沉降槽面积相等,此时可认为轨枕未与道砟脱空,而随着路基沉降量的增加轨道沉降槽面积增量逐渐减小,出现轨枕空吊现象.根据轨面沉降数据分析结果可知,采用本文所提的轨枕临界空吊时路基不均匀沉降面积临界值估算方法来设计试验工况是可行性的.
第2组试验所得轨道变形如图8b所示,3条沉降曲线所围成的面积增量基本相等,说明随着路基不均匀沉降槽面积的等量增加钢轨沉降槽面积的增加量也相等.进一步分析知,路基沉降曲线面积与轨道沉降曲线面积之比约为1,说明在本试验条件下最终沉降变形稳定阶段道砟的前后密实状态相同,同时也说明此时不产生轨枕空吊.
第3组试验结果与第1 组试验定性规律相似,但从图8a与图8c沉降曲线对比可得,两组试验的第2个工况路基沉降槽面积增量所引起的轨道沉降槽面积增量都比第1个工况情况下轨道沉降槽面积增量小,说明第2个工况情况下,路基沉降槽面积的增量与轨面沉降槽面积的增量存在一定的差值,而这部分面积差将引起轨枕的空吊与道砟的松散,但由于道砟厚度较小,道床变形稳定后道砟松散所引起的面积变化量较小,因此可判断在第2个工况情况下轨枕将产生空吊现象.同时,从图8a与图8c的对比可知,第3组试验的第2个工况所引起的轨道沉降变形增量明显比第1 组试验要小,说明第3组试验轨枕空吊量较大,试验过程中第3组试验观察到明显的轨枕空吊现象,且最大的轨枕空吊量较大,约为65mm,如图9所示.

表2 路基不均匀沉降槽与轨面沉降槽的参数对比Tab.2 Contrast of subgrade differential setting tank parameters and track setting tank parameters

图8 路基不均匀沉降引起轨面的变形Fig.8 Track settlement caused by subgrade differential settlement

图9 轨枕空吊现象Fig.9 Phenomenon of unsupported sleeper
对表2数据进行进一步分析可得,轨面与路基不均匀沉降槽曲线的面积比随路基不均匀沉降面积变化的关系如图10所示,路基的不均匀沉降槽面积较小且并未引起轨枕空吊时,轨面与路基纵向不均匀沉降槽的面积比为1,随着路基不均匀沉降继续增加,当轨面与路基纵向不均匀沉降槽的面积比小于1时,有砟轨道将出现轨枕空吊现象,并且面积比将随路基不均匀沉降的增加而减小.以本试验为例,当路基不均匀沉降的面积小于0.016m2时,面积比近似为1,表明道砟在试验前后两种稳定状态的密实程度不发生变化;当路基不均匀沉降的面积大于0.016 m2时,该面积比随路基不均匀沉降面积的增大而减小,表明随道路基不均匀沉降的面积的增大,有更多的变形不能反映到钢轨面上,将出现轨枕空吊现象.由以上分析知,在试验荷载作用下,当路基不均匀沉降曲线的面积与钢轨面沉降曲线的面积比由近似为1的值开始减小时,所对应的路基不均匀沉降的面积为轨枕出现空吊的临界值.通过对结果及数据的分析,可确定在试验条件下,这个临界值在路基不均匀沉降面积为0.016~0.032m2之间,即出现轨枕吊空现象时,对应于波长为2.43m 的余弦型路基不均匀沉降,波幅为13.19~26.39 mm 之间的某一个值.
2.3 余弦型路基不均匀沉降发生后轨面沉降计算
(1)轨枕脱空情况
当路基不均匀沉降较大时将引起轨枕的空吊现象,此时作用于轨枕下方的道砟上的动荷载较未脱空时小,导致最终变形稳定状态道砟的密实程度变小,引起道砟的体积变大,在线路纵断面上表现为道砟有ΔS的面积增量.结合图3进行分析,此时道砟面的沉降槽面积S2不等于钢轨面沉降槽的面积S3,其差值ΔS′即为轨枕与道砟面脱空的空隙在纵断面所形成的面积,因此路基沉降槽的面积可表示为

轨枕空吊情况下,道砟的体积变化涉及诸多因素,如动荷载的作用、路基沉降特性、道砟材料的物理力学特性等,限于试验条件,本试验无法对这些因素的影响展开研究.同时,由于道砟体积变化量及轨枕空吊引起的空隙的大小都难以在试验中进行量测,因此仅从本试验结果分析无法给出余弦型路基不均匀沉降引起轨枕空吊情况下轨面不均匀沉降的确切计算公式,但是该问题值得进一步研究.
(2)轨枕未脱空情况
轨枕未脱空情况下,显然ΔS′=0,根据前面试验结果可知,当路基不均匀沉降小于引起轨枕发生空吊的路基不均匀沉降临界值时,路基不均匀沉降槽的面积与最终钢轨面的变形槽的面积相等.未出现轨枕脱空时,近似余弦型路基不均匀沉降在一定动荷载作用下,可认为在轨道变形稳定前后道砟的体积不发生变化ΔS=0,整个轨道结构纵向变形可采用光滑余弦型曲线表示,路基的沉降在道砟中成一定的角度向上扩散.因此,只要知道路基的沉降大小和道砟的变形扩散特性,即可得到轨道的累积沉降变形大小.
取全波余弦型路基不均匀沉降的波长为l1,波幅为δ1,全波余弦型轨面沉降槽的波长为l2,波幅为δ2,道砟的变形扩散角为φ,道砟厚度为b,轨枕高为h,则有

根据式(2),由路基不均匀沉降槽的面积与钢轨面的变形槽的面积相等,即:

从而可求出路基不均匀沉降引起轨面沉降槽曲线的波幅δ2的大小:

当路基沉降曲线为余弦型曲线且曲线的表达式已知时,根据式(3)~(5)可计算钢轨面余弦型沉降曲线的表达式.
在式(3)~(5)中,道砟的变形扩散角是其中重要的参数之一.在本试验中(见表2),路基沉降槽宽度外延两跨轨枕的纵向长度(约1.2 m 左右)即为钢轨沉降的受影响范围.此时路基沉降变形在道砟中的传播扩散角在第1、3 组中约为26°,第2 组中约25°.显然,这与道砟的自然休止角相差较大,且角度较小,它可能是由于以下两方面的原因引起的:第一,本试验轨道沉降变形测点的纵向间距较大(约0.6 m),因此所取观察点未必是轨面沉降变形宽度的实际端点;第二,由于激振动荷载的作用,使道砟颗粒的自稳性变差,休止角变小,那么道砟变形扩散角亦变小,这与道砟的材质、级配、颗粒大小及所受动荷载类型等因素不无关系,因此仅通过本试验难以明确其变化机理,有待结合其他研究手段进一步研究.
3 结论
(1)试验结果表明,路基产生一定波长的余弦型不均匀沉降时,由路基沉降引起的轨道沉降变形曲线可用余弦型函数描述.
(2)通过试验研究发现,一定路基不均匀沉降情况下有轨枕空吊现象出现的可能.在本试验中,波长2.43m 的余弦型路基不均匀沉降引起轨枕出现空吊的临界波幅在13.19~26.39mm 之间.
(3)试验结果表明,路基的不均匀沉降槽面积小于引起临界轨枕空吊的路基不均匀沉降槽的面积时,轨面与路基纵向不均匀沉降槽的面积比约为1,说明在同一动荷载长期作用下,路基变形较小时,路基产生变形前后道砟密实状态不发生明显变化.
(4)根据试验结果,提出路基不均匀沉降不引起轨枕空吊情况下有砟轨道沉降变形的计算公式.计算公式中关键参数为道砟变形扩散角,本试验条件下,测得路基不均匀沉降对应的变形在道砟中的传播角度约为26°,然而道砟的扩散角与道砟的级配、材质、密实程度及所受动荷载的特性有关,道砟变形扩散的机理及道砟变形扩散角的大小有待进一步研究明确.
[1] 张群.路基不均匀沉降对双块式无碴轨道的影响研究[D].成都:西南交通大学道路与铁道工程系,2007.ZHANG Qun.Study of doubleblock ballastless track causing by subgrade differential settlement[D].Chengdu:Southwest Jiaotong University.Department of Road and Railway Engineering,2007.
[2] Dahlberg T.Some railroad settlement models 2acritical review[C]//Proceeding of the Institution of Mechanical Engineering,Part F,Journal of Rail and Rapid Transit.London:Professional Engineering Publishing House,2001(F4):215-289.
[3] 杉山德平.鉄道技術研究報告No.1081 軌道狂い進みの実とその解析[R].东京:鉄道技術研究所,1978.
[4] 内田雅夫,石川達也,三和雅史.軌道狂い進みに着目した有道床軌道の新しい設計法[J].鉄道総研報告,1995,9(2):37.
[5] 蔡成标,翟婉明,赵铁军,等.列车通过路桥过渡段时的动力作用研究[J].交通运输工程学报,2001,1(1):17.CAI Chengbiao,ZHAI Wanming,Zhao Tiejun,et al.Research on dynamic interaction of train and track on roadbed-bridge transition section[J].Journal of Traffic and Transportation Engineering,2001,1(1):17.
[6] Kerr A D,Moroney B E.Track transition problems and remedies[J].Bulletin 742-American Railway Engineering Association,1995(742):267.
[7] Monley G J,Wu T H.Tensile-reinforcement effects on bridgeapproach settlement[J].Journal of Geotechnical Engineering,1993,119(2):749.
[8] 李献民,王永和,杨果林,等.高速下过渡段路基动响应特性研究[J].岩土工程学报,2004,26(1):100.LI Xianmin,WANG Yonghe,YANG Guolin,et al.Study on the dynamic response of transition section roadbed subject to high speed[J].Chinese Journal of Geotechnical Engineering,2004,26(1):100.
[9] 韩义涛,姚力.基础沉降对土路基上板式轨道动力性能影响分析[J].铁道工程学报,2007,10:28.HAN Yitao,YAO Li.Analysis of the dynamic perfor-mance for slab track settlement on embankment[J].Journal of Railway Engineering Society,2007,10:28.
[10] 翟婉明,韩卫军,蔡成标,等.高速铁路板式轨道动力特性研究[J].铁道学报,1999,21(6):65.ZHAI Wanming,HAN Weijun,CAI Chengbiao,et al.Dynamic properties of high-speed railway slab tracks[J].Journal of the China Railway Society,1999,21(6):65.
[11] Shenton MJ.Deformation of railway ballast under repeated loading conditions[R].London:British Railways Research and Development Division,1974.

