模型再生混凝土单轴受压性能细观数值模拟
肖建庄,李文贵,刘 琼
(1.同济大学 建筑工程系,上海200092;2.同济大学 先进土木工程材料教育部重点实验室,上海200092)
再生混凝土技术对于建筑业的可持续发展以及我国节约型社会的构建具有重要意义,是发展绿色生态混凝土的主要措施之一[1].
与普通混凝土相比,再生混凝土是一种细观结构更为复杂的5 相复合材料,主要包括:天然粗骨料、老硬化水泥砂浆、新硬化水泥砂浆、老界面过渡区(老ITZ)和新界面过渡区(新ITZ)[2].国内外研究者发现再生混凝土的抗拉、抗压强度以及弹性模量较普通混凝土有所降低[3].因此,有必要在细观层次上研究再生混凝土的破坏过程,从而揭示其破坏特征和机理.
1 模型再生混凝土
1.1 模型再生混凝土的概念
基于Buyukozturk等[4]研究含有9颗圆骨料规则分布的普通混凝土模型,本文提出了模型再生混凝土的概念,见图1.再生粗骨料的布置要考虑骨料之间的净距离d与骨料半径r满足一定的关系:d=(0.1~0.3)r.
1.2 再生混凝土的各相特性
再生混凝土的细微观结构对再生混凝土的强度有重要影响[5].天然粗骨料的弹性模量取50~100 GPa,抗拉强度取1.4~14 MPa,抗压强度取70~350 MPa是比较合适的[6];硬化水泥砂浆的力学性能在很大程度上影响再生混凝土的宏观力学性能,其弹性模量在10~30GPa之间[7];采用扫描电子显微镜和X 射线衍射仪可以得到混凝土中ITZ 厚度约为40~50μm[8].Lutz等的三相模型研究显示,ITZ的弹性模量是砂浆基体弹性模量的30%~50%[9].Rasheeduzzafar等认为再生混凝土中的新ITZ强度高于老ITZ的强度[10].

图1 模型再生混凝土示意图(单位:mm)Fig.1 Diagram of modeled recycled concrete(unit:mm)
2 有限元建模与参数设置
2.1 有限元模型
采用Ansys有限元软件,天然粗骨料和新老硬化砂浆采用Solid185 实体单元,新老ITZ 采用Solid65实体单元;新老硬化水泥砂浆单元采用弹塑性材料模型、等向强化的Von Mises屈服准则和Willam-Warnke参数破坏准则;新老ITZ单元考虑开裂失效,采用William-Warnke参数破坏准则;模型再生混凝土受破坏后,水泥砂浆采用各向同性的损伤模型,界面过渡区采用弥散裂缝形式的损伤本构.模型共有18 832 个单元,其中天然骨料单元8 064个,老ITZ 单元1 152 个,老硬化砂浆单元3 456个,新ITZ 单元1 152 个,新硬化砂浆5 008个,见图2.有限元模型顶部X、Y向位移自由;底部约束Y方向的自由度,且约束试件底部边缘中间节点X向自由度.在Y方向施加竖向位移荷载,选择静力分析.打开大变形,加载位移为0.045 mm·步-1.Cnvtol采用位移收敛准则,收敛精度缺省值是0.5%.采用完全的Newton-Raphson 平衡迭代进行非线性求解,荷载步选项中Nsubst的制定子步数为100,最大子步数为200,最小子步数为50.

图2 模型再生混凝土有限元模型Fig.2 Finite element model of modeled recycled concrete
2.2 细观本构与力学参数设置
模型再生混凝土中天然粗骨料的粒径为20 mm,在加载过程中一般不会破坏[11],从而始终假定其本构关系为线弹性.新老硬化水泥砂浆受压、受拉本构模型根据单轴受力试验确定,如图3~图4 所示.再生混凝土中老硬化砂浆的含量与再生混凝土某一截面处的老硬化砂浆的面积百分比基本相等,老硬化砂浆的厚度取2.5mm,再生骨料中老硬化砂浆的体积含量约为36%[12];新老硬化砂浆的泊松比取0.22.新老ITZ厚度取50μm,取ITZ的强度和弹性模量约为硬化砂浆的50%.设ITZ的受拉细观本构关系为弹脆性,泊松比取0.20.为避免模型参数太多,假设5相介质材料相应的细观力学参数见表1.

图3 硬化砂浆单压本构关系Fig.3 Constitutive relationship for hardened mortar under compression
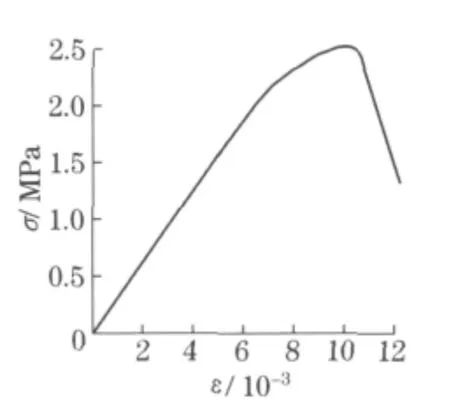
图4 硬化砂浆单拉本构关系Fig.4 Tensile constitutive relationship for hardened mortar under tension

表1 模型再生混凝土各相材料细观力学性能Tab.1 Meso-level mechanical properties of each phase in modeled recycled concrete
3 破坏过程模拟与机理分析
对再生混凝土的单向受压过程进行数值模拟分析,计算过程中共有52个荷载子步,计算过程大约需要300min(计算机主要硬件配置,CPU:Pentium(R)Dual E2140 1.60GHz;SDRAM:2×1GDDR2-667;Mother board:SIS672).UY(Y向位移)分布云图可以反映模型再生混凝土内部各相材料的变形情况;SY(Y向主应力)分布云图可以反映模型再生混凝土在受力过程中内部应力的发展与重分布情况.对数值模拟结果进行后处理,在荷载子步为15和39时,分别提取UY位移和SY主应力云图,如图5和图6所示.

图5 Y 向位移云图(共52子步)(单位:mm)Fig.5 Displacement contour map in Y direction (52subsets in sum)(unit:mm)

图6 Y 向主应力分布(共52子步)(单位:MPa)Fig.6 Principal stress distribution in Y direction (52subsets in sum)(unit:MPa)
由如图5可知,在初始加载阶段,模型的变形比较均匀.随着荷载的增大,由于各相材料的力学性能的差异,在Y向出现相对错动.当ITZ不能承受由于错动引起的应力,将在强度薄弱处出现裂缝,之后在ITZ区域发生破坏.裂缝随着荷载的增大,逐渐向硬化砂浆部位扩展.
由如图6可知,在模型再生混凝土单向受压的初始阶段,5相介质材料均处于线弹性状态,同相介质的应力分布基本一致.随着荷载的增大,模型再生混凝土各相的应力分布不均匀.在加载过程中,裂缝开展处应力不均匀分布,而远离裂缝处的应力分布则相对稳定.
4 单轴受压性能变参数仿真分析
假设5相介质材料的强度与弹性模量相关,选取再生粗骨料取代率、新硬化砂浆强度、老硬化砂浆强度、老硬化砂浆厚度以及新老ITZ 强度等为模拟对比参数,模型再生混凝土仿真试件的变参数情况见表2.

表2 细观力学变参数一览表Tab.2 List of meso-level mechanical parameter variations
4.1 再生粗骨料取代率
试件NC-1-1,RC-1-2和RC-1-3的再生粗骨料取代率分别为0,55.6%和100%.通过数值模拟计算表明(图7):随着再生粗骨料取代率的提高,模型再生混凝土的初始弹性模量依次降低;与NC-1-1相比,RC-1-2 和RC-1-3 的初始弹性模型分别降低2.26%,3.99%;模型再生混凝土的峰值应力也依次减少,分别降低1.68%,1.77%,这与试验结果相吻合[11-12];峰值应变的变化规律不明显,依次为0.001 54,0.001 49和0.001 54.

图7 再生粗骨料取代率对单轴受压性能的影响Fig.7 Influence of recycled aggregate replacement on the compressive behavior
4.2 新硬化水泥砂浆强度
如图8所示,随着新硬化砂浆强度的提高,模型再生混凝土的初始弹性模量依次增大,与RC-3-1相比,RC-2-2,RC-2-3 的初始弹性模型分别增大11.20%,21.31%;模型再生混凝土的峰值应力依次增大,分别提高62.25%,82.38%,这与再生混凝土的宏观力学试验结果相吻合[12-13].峰值应变依次为0.001 07,0.001 54和0.001 15,随着新硬化砂浆强度的提高,峰值应变的变化规律不明显,除新硬化砂浆强度外,这可能还与新老硬化砂浆之间的强度差有关.

图8 新硬化砂浆强度对单轴受压性能的影响Fig.8 Influence of the strength of new hardened mortar on the compressive behavior
4.3 老硬化水泥砂浆强度
如图9所示,随着老硬化砂浆强度的提高,再生混凝土的初始弹性模量依次增大,与RC-3-1相比,RC-3-2,RC-3-3的初始弹性模型分别增大5.04%,8.90%;模型再生混凝土的峰值应力依次增大,分别提高67.51%,68.55%.这与再生混凝土的宏观力学试验结果相吻合[12,14].峰值应变依次为0.000 87,0.001 54和0.001 23,随着老硬化砂浆强度的提高,峰值应变的变化规律不明显,除老硬化砂浆强度外,这可能还与新老硬化砂浆之间的强度差有关.

图9 老硬化砂浆强度对单轴受压性能的影响Fig.9 Influence of the strength of old hardened mortar on the compressive behavior
4.4 老硬化水泥砂浆厚度
如图10所示,随着老硬化砂浆厚度的增大,模型再生混凝土的初始弹性模量依次减少,与RC-4-1相比,RC-4-2,RC-4-3 的初始弹性模型分别降低2.20%,4.53%;峰值应力也依次减少,分别降低1.58%,2.94%.这与再生混凝土的宏观力学试验结果相吻合[15].峰值应变依次为0.001 59,0.001 54和0.001 54.由此可知,随着老硬化砂浆厚度的增大,模型再生混凝土的峰值应变稍有降低.
4.5 界面过渡区强度
如图11所示,随着界面强度的提高,模型再生混凝土的初始弹性模量稍有提高,与RC-5-1相比,RC-5-2,RC-5-3的初始弹性模型分别提高0.76%,1.10%;峰值应力也依次增大,分别提高0.20%,0.36%.这与再生混凝土的宏观力学试验结果相吻合[16].峰 值 应 变 依 次 为0.001 54,0.001 54 和0.001 54.由此可知,随着界面强度的增大,再生混凝土的峰值应变变化不大,说明提高界面过渡区的强度对初始弹性模量、峰值应力和峰值应变的影响并不十分显著.
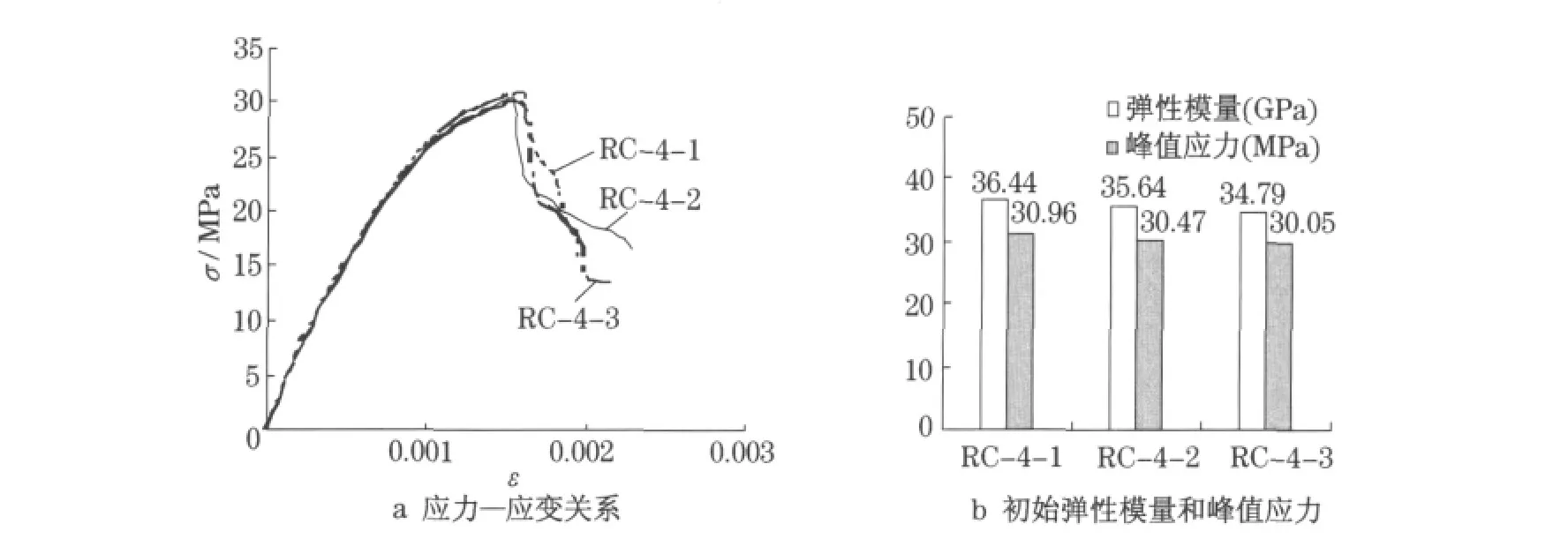
图10 老硬化砂浆厚度对单轴受压性能的影响Fig.10 Influence of the thickness of old hardened mortar on the compressive behavior

图11 界面过渡区强度对单轴受压性能的影响Fig.11 Influence of the strength of ITZs on the compressive behavior
5 结论
对模型再生混凝土的单向受压性能进行了细观数值模拟与计算分析,可得到以下结论:
(1)模型再生混凝土最先在较为薄弱的界面过渡区处产生裂缝,然后向老硬化水泥砂浆扩展,最后延伸到新硬化水泥砂浆;
(2)随着再生粗骨料取代率增大,模型再生混凝土的初始弹性模量和峰值应力均有小幅降低;
(3)增大新硬化砂浆的强度,模型再生混凝土的初始弹性模量和峰值应力均有大幅提高;提高老硬化砂浆的强度,模型再生混凝土的初始弹性模量和峰值应力均增大,其峰值应力的增大较为显著;随着老硬化砂浆厚度增大,模型再生混凝土的初始弹性模量和峰值应力均降低,峰值应变稍有降低;
(4)提高界面过渡区的强度,模型再生混凝土的初始弹性模量、峰值应力和峰值应变的影响并不十分显著;
(5)在其他因素相同的情况下,新老硬化水泥砂浆的强度对再生混凝土抗压强度有较大影响.在老砂浆满足强度要求时,建议新配制再生混凝土的强度与废混凝土的强度接近.
[1] 肖建庄.再生混凝土[M].北京:中国建筑工业出版社,2008.XIAO Jianzhuang.Recycled concrete[M].Beijing:China Architecture & Building Industry Press,2008.
[2] 肖建庄,刘琼,李文贵,等.再生混凝土细微观结构和破坏机理研究[J].青岛理工大学学报,2009,30(4):24.XIAO Jianzhuang,LIU Qiong,LI Wengui,et al.On the microand meso-structure and failure mechanism of recycled concrete[J].Journal of Qingdao Technological University,2009,30(4):24.
[3] 肖建庄.再生混凝土单轴受压应力—应变全曲线试验研究[J].同济大学学报:自然科学版,2007,35(11):1445.XIAO Jianzhuang.Experimental investigation on complete stress-strain curve of recycled concrete under uniaxial loading[J].Journal of Tongji University:Natural Science,2007,35(11):1445.
[4] Buyukozturk O,Nilson A H,Slate F O.Stress-strain response and fracture of a concrete model in biaxial loading[J].ACI Journal,1971,68(8):590.
[5] Tama V W Y,Gaob X F,Tama C M.Microstructural analysis of recycled aggregate concrete produced from two-stage mixing approach[J].Cement and Concrete Research,2005,35(6):1195.
[6] 吴科如,张雄.建筑材料[M].上海:同济大学出版社,1994.WU Keru,ZHANG Xiong.Building materials[M].Shanghai:Tongji University Press,1994.
[7] Olley P.Construction materials reference book [M].Butterworth:Oxford Press,1992.
[8] Maso J C.Interfacial transition zone in concrete[R].Toulouse:E & FN Spon,1996.
[9] Lutz MP,Monteiro P J M,Zimmerman R W.Inhomogeneous interfacial transition zone model for the bulk modulus of mortar[J].Cement Concrete Research,1997,27(7):1117.
[10] Rasheeduzzafar I B,Khan A.Recycled concrete——a source for new aggregate[J].Cement Concrete and Aggregates(ASTM),1984,6(1):17.
[11] 肖建庄,李佳彬,孙振平,等.再生混凝土的抗压强度研究[J].同济大学学报:自然科学版,2004,32(12):1558.XIAO Jianzhuang,LI Jiabin,SUN Zhenping,et al.Study on compressive strength of recycled aggregate concrete[J].Journal of Tongji University:Natural Science,2004,32(12):1558.
[12] Hansen T C.Recycled aggregate and recycled aggregate concrete(second state of art report,development from 1945-1985)[J].Material and Structures,1986,19(5):20.
[13] Tu T Y,Chen Y Y,Hwang C L.Properties of HPC with recycled aggregates[J].Cement and Concrete Research,2006,36(5):943.
[14] Etxeberria M,Vázquez E,MaríA,et al.Influence of amount of recycled coarse aggregates and production process[J].Cement and Concrete Research,2007,37(5):735.
[15] Tam W Y V,Tam C M,Le K N.Removal of cement mortar remains from recycled aggregate using pre-soaking approaches[J].Resources,Conservation and Recycling,2007,50(1):82.
[16] Poon C S,Shui Z H,Lam L.Effect of microstructure of ITZ on compressive strength of concrete prepared with recycled aggregates[J].Construction and Building Materials,2004,18(6):461.

