具有均匀量化器的网络控制系统的一致有界性

刘俊豪, 张 皓, 陈启军

(同济大学 电子与信息工程学院, 上海201804)

在网络控制系统中,传感器采集到的信号和控制器产生的信号都需要通过网络传输.对于连续被控对象,信号传输前必须进行采样、量化、编码,从而不可避免地带来量化误差;同时, 网络中的丢包、时延、乱序、误码等因素也会对系统性能产生影响, 对这些网络控制系统特有的性能的研究成为一个新的热点研究方向[1-6].

目前,针对网络控制系统量化的研究主要分为3种:一种是早期针对实际中使用的量化器进行的一些初步的研究.文献[7] 将量化误差分解为不同的部分,并详细分析了量化误差对信号的影响.文献[8] 通过调节控制律巧妙地消除了量化误差的影响,从而实现了系统的镇定.文献[9] 讨论了在量化误差影响下的非线性系统的有界性问题.文献[10] 考虑量化误差的影响,设计控制器使系统收敛在一定范围内.然而,这些文献都没有考虑网络控制系统中的时延、丢包等因素.另一种研究方法是文献[11-12] 提出的将量化误差转换为与系统状态相关的不确定性来处理的方法.通过这种转换,可以将量化误差问题转化为传统的鲁棒控制问题, 从而实现对系统的镇定、观测及性能优化等.然而,这种转换需要量化器在平衡点处无限细化,从而在平衡点附近有无限级别, 这种量化器会产生无限长的编码, 这在实际使用时无法实现.还有一种方法是Daniel Liberzon 等[13]、翟贵生等[14]提出的区域量化方法, 该方法将被量化信号分为若干个区域,通过不断调节一个比例参数来实现系统的镇定.为了有效地解码, 这种方法要求该比例参数能够及时、精确地从编码端发送到解码端,而实际网络控制系统无法实现这点(因为比例参数传输前必须进行量化,必定会产生量化误差;同时网络的存在会产生时延、丢包等影响,无法实现实时传输).

根据上面的分析可以看出, 目前针对网络控制系统量化的研究中,第1 种早期的研究方法没有考虑网络特性对系统的影响;另外2 种方法从理论上对网络控制系统进行了一系列的研究, 然而无法在实际中实现.如果同时考虑实际应用中的量化方式以及网络控制系统的特性,对系统的镇定将很困难,这也是目前还没有文献将这2 个方面同时考虑的一个重要原因.在实际应用中系统往往允许存在一定的误差,只要系统状态能够控制在一定的范围内即可,不必要渐近收敛于平衡点.系统的一致有界性控制是指通过一定的控制策略将系统状态控制在一个与初始时刻无关的范围内.因此, 针对实际要求, 可以不实现系统的渐近稳定,转而设计控制方法使网络控制系统一致有界.这样既满足实际要求, 又可以使设计方法变得可行.本文实现了在不考虑量化条件下对网络控制系统的镇定以及考虑均匀量化情况下的一致有界性控制.通过仿真实例验证了所提方法的有效性,分析了量化误差对系统收敛的影响.

1 系统描述

网络控制系统的结构主要包括被控对象、传感器、采样器、量化器、编码器、解码器、控制器以及执行器,网络中存在时延、丢包、乱序等特性.传感器从被控对象采集到信号经过网络传输到控制器.控制器根据从传感器得到的信号确定控制策略,再经过网络传输到执行器, 从而实行对被控对象的控制.

假设:①传感器为时间驱动, 控制器、执行器为事件驱动;②控制回路时延(把丢包归入时延中)为短时延,即控制回路总时延小于1 个采样周期.

对于线性连续被控对象, 忽略量化的影响, 网络控制系统模型建立为

式中:x(t)为被控对象状态,x(t)∈Rn;u(t)为控制信号,u(t)∈Rm;A ,B 为适维矩阵.

由于被控对象是连续对象, 而传输过程为离散过程.因此,采用离散化方法, 将模型(1)离散化为

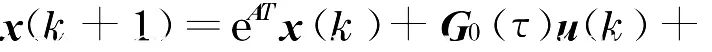
式中:k为离散化时间变量;T为采样周期;τ为控制回路总时延;

因此, 式(2)可表示为

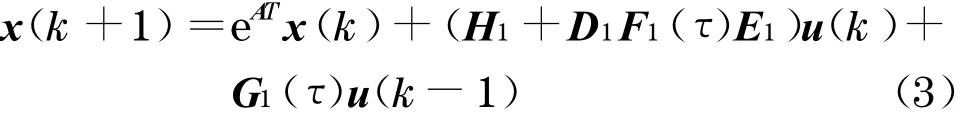
控制器方程表示为

式中:K1,K2为适维的常数矩阵.

结合式(3),网络控制系统可表示为

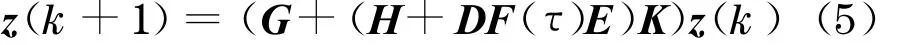
考虑实际中使用的均匀量化器[7-8].均匀量化器q(v)可用表示为

式中:v 为被量化的信号, v ∈Rn×1;Δ(v)为量化误差, Δ(v)的第i维元素≤δi, δi＞0 为每一维的量化误差上界.从而,

考虑从传感器到控制器的量化误差的影响, 式(4)可表示为

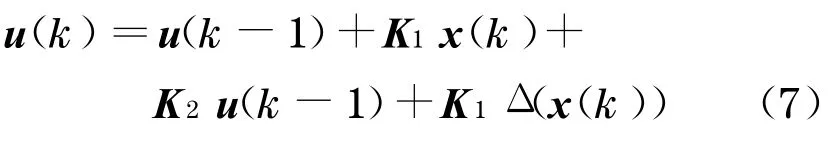
考虑从控制器到执行器的量化误差的影响, 被控对象离散化方程(2)可改写为

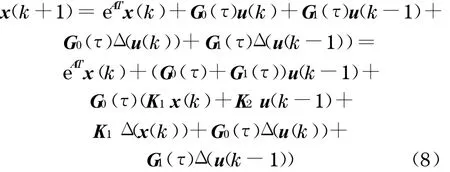
结合式(7)、式(8),包含均匀量化器的网络控制系统的状态方程为

2 网络控制系统的稳定性及一致有界性

根据文献[15-16] 可得系统一致有界性定义.

定义1 若对∀α＞0,存在β(k0,α)＞0,使得当‖z(k0)‖ ≤α时, 系统(9)的解‖ z(k,k0,z(k0))‖ ≤β(k0,α),k＞k0,则称系统(9)等度有界;若β(k0,α)与k0无关,则称系统(9)一致有界.

引理1[14]对于给定的对称矩阵Y 及适维矩阵M, N, W,WTW ≤I,如 果满足Y +MWN +NTWT·MT＜0 ,则存在一个常数ε＞0,使得

引理2 设矩阵,其中‖ · ‖为Frobenius 范数.r =[r1r2 …r n]T∈Rn,s =[s1s2 …s n]T∈Rn为任意的n维向量, 满足,则‖Mr +Ns ‖ ≤‖M+N ‖· ‖l ‖.

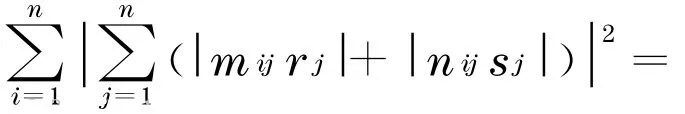
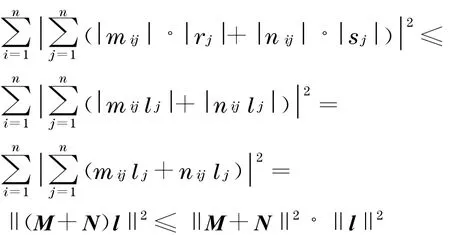
定理1 对于网络控制系统(5), 如果存在矩阵X ＞0 及常数ε＞0 满足

则网络控制系统(5)渐近稳定.

即

根据引理1,可得

上式等价于式(10).因此, 式(10)成立等价于V(z(k+1))-V(z(k))＜0 ,则系统(5)渐近稳定.

定理2 对于考虑均匀量化器的的网络控制系统, 假设整个系统采用相同的量化器, 即, 令.对于系统模型(9), 如果存在矩阵X ＞0,Q＞0 及常数ε＞0 满足

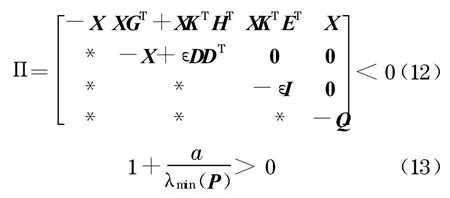
则网络控制系统(9)一致有界.并且,令初始时刻为k0、初始状态为z(k0), 当k＞k0时,

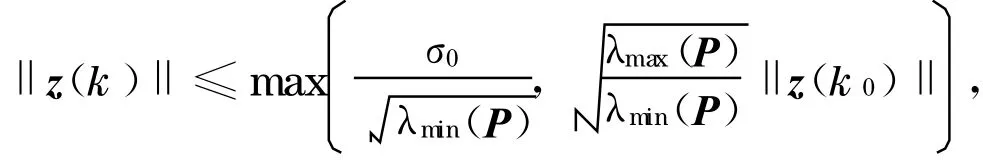
式中:λmin(P), λmin(Q)表示矩阵P ,Q 的最小特征值,.利用引理2 ,得

证明:定义函数V(z(k))=zT(k)Pz(k),其中,P ＞0 .根据系统模型(9),使用类似定理1 的证明方法可得

如果式(12)成立,可得

根据式(13)及b＞0,可得

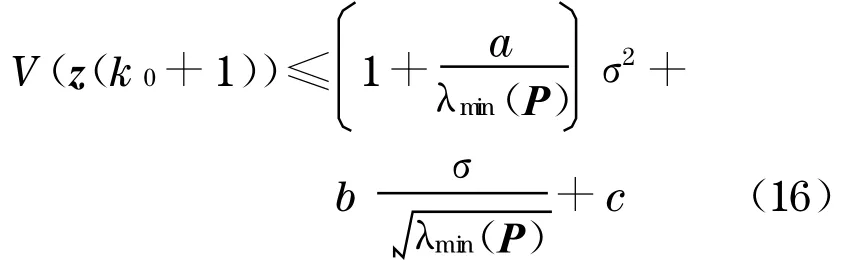
由于σ≥σ0,结合式(14)中关于σ0定义,得

同理递推, 可得k＞k0时,V(z(k))≤σ2.从而

对∀α＞0,‖z(k0)‖ ≤α时,存在与k0 无关的

使得系统(9)的解‖z(k,k0,z(k0))‖ ≤β(k0,α),k＞k0,根据定义1 可知系统(9)一致有界, 定理得证.

从定理2 可以看出, 考虑量化影响的网络控制系统当满足式(12)、式(13)条件时, 是一致有界的,定理2 给出了系统收敛的一个上界, 该上界与初始值和量化误差有关.因此, 可以根据实际要求, 设计相应的量化级别,在确定信号的最大最小值后,便可以求出所需的量化误差及编码长度.在满足实际要求的前提下, 增大量化误差, 可以减少编码长度, 从而减少网络中传输的数据量, 以减少网络拥塞和丢包,降低网络时延.

3 仿真实例

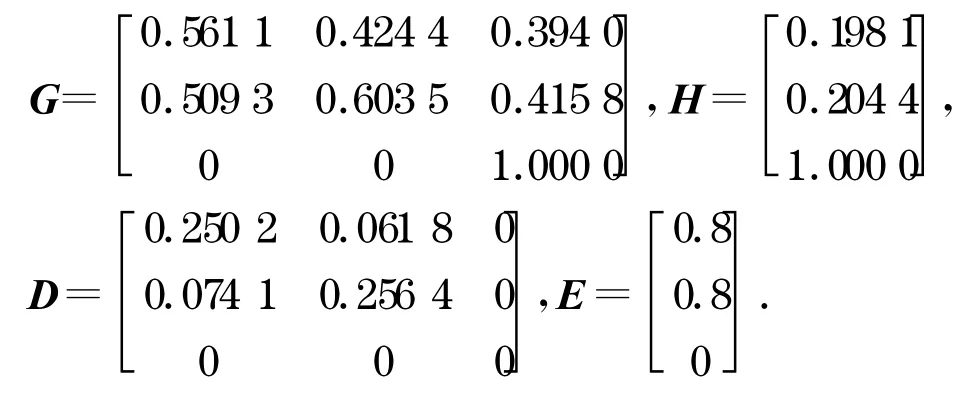
根据定理1,可得

图1a 绘制了被控对象状态曲线, 从中可以看出被控对象是稳定的.

图1 被控对象状态曲线Fig .1 State of networked control systems

取δ=0 .01 ,根据定理2,求得

‖z(k)‖ ≤0.445 0.可以验证a/ λmin(P)=-0.421 8 ,式(13)成立.图1b绘制了被控对象状态曲线,可以看出系统状态最终收敛在一定的范围内.从定理2 可以看出,被控系统收敛的情况与初值和量化误差有关,图2 绘制了δ=0 .01 和δ=0.10时被控对象状态x1(t)的曲线,从中可以看出量化误差越大,系统收敛情况越差,用同样的方法观察被控对象状态x2(t),也可得到同样的结论.

图2 不同的量化误差的被控对象状态Fig.2 State of networked control systems with different quantized error

4 结论

针对网络控制系统建立了模型, 在忽略量化误差影响的情况下, 设计了使系统渐进稳定的控制方法.在实际使用中, 考虑到量化误差的影响, 由于网络控制系统时滞、丢包等因素的影响,系统的镇定变得很困难, 本文根据实际使用中往往不需要系统状态渐近收敛到平衡点的情况, 在考虑均匀量化器的情况下,实现了系统一致有界控制.得出的收敛上界与系统的初始状态和量化误差有关, 可以根据实际使用要求来设计通信中的量化级别和编码长度.通过仿真验证了所提方法的有效性, 并从仿真图可直观看出量化误差对系统收敛的影响.

[1] GAO H uijun, CH EN T ongw en.A new approach to quantized feedback control systems[J] .Automatica,2008, 44(2):534.

[2] 李静, 史建国, 左斌.具有参数不确定性的长时延网络控制系统研究[J] .系统仿真学报, 2009, 21(12):3684.LI Jing,SH I Jianguo,ZUO Bin.Research on networked control system s with long time delay and parameter uncertainties[J] .Journal of Sy stem Simulation, 2009, 21(12):3684.

[3] 于之训, 陈辉堂, 王月娟.基于H∞和μ综合的闭环网络控制系统的设计[J] .同济大学学报:自然科学版, 2001, 19(2):307.YU Zhixun, CHEN Huitang, WANG Yuejuan.Design of closed loop network control system based on H∞and μsynthesis[J] .Journal of T ongji University:Natural Science, 2001, 19(2):307.

[4] 邱占芝, 张庆灵, 杨春雨.基于广义系统的网络控制系统的分析与建模[J] .东北大学学报:自然科学版, 2005, 26(5):409.QIU Zhanzhi, ZHANG Qingling, YANG Chunyu.Analysis and modeling of networked control systems based on descriptor system [J] .Journal of Northeastern University:Natural Science, 2005, 26(5):409.

[5] 马卫国, 邵诚.网络控制系统随机稳定性研究[J] .自动化学报.2007, 33(8):878.MA Weiguo, SHAO Cheng.Stochastic stability for networked control systems[J] .Acta Automtica Sinica, 2007, 33(8):878.

[6] 邓玮璍, 费敏锐.非线性网络控制系统的T-S 模糊H∞控制与数值仿真[J] .系统仿真学报, 2010, 22(7):1651.DENG Weihua, FEI Minrui.T-S fuzzy H∞control and numerical simulation of nonlinear networked control systems[J] .Journal of System Simulation, 2010, 22(7):1651.

[7] WONG Pingwah.Quantization noise, fixed-point multiplicative round off noise, and dithering [J] .IEEE Transaction on Acoustics Speech, and Signal Proceessing, 1990, 38(2):286.

[8] Poogyeon Park, Yun Jongchoi, Sung Wookyun.Eliminating effect of input quantisation in linear systems[J] .Electronics Letters, 2008, 44(7):456.

[9] Hou Ling, Anthony N Michel, Ye Hui.Some qualitative properties of sampled-data control systems [J] .IEEE Transactions on Automatic Control, 1997, 42(12):1721.

[10] YU Hongwang, WANG Zhiming, DAI Haohui. Floatingquantization effects on sampled-data nonlinear control systems[C] ∥8th International Conference on Control, Automation,Robotics and V ision. Kunming: Nanyang Technological University, 2004:1669-1673.

[11] FU Minyue, XIE Lihua.T he sector bound approach to quantized feedback control[J] .IEEE Transactions on Automatic Control,2005, 50(11):1698.

[12] Elia Nicola, Mitter Sanjoy K.Stabilization of linear systems with limited information[J] .IEEE Transactions on Automatic Control, 2001, 46(9):1384.

[13] Daniel Liberzon, Dragan Nesic.Input-to-state stabilization of linear systems with quantized state measurements[J] .IEEE Transactions on Automatic Control, 2007, 52(2):767.

[14] 陈宁, 翟贵生, 桂卫华, 等.不确定关联网络系统分散H∞量化控制[J] .控制与决策, 2010, 25(1):59.CHEN Ning, ZHAI Guisheng, GUI Weihua, et al.Decentralized H∞quantized control for uncertain interconnected networked systems[J] .Control and Decision, 2010, 25(1):59.

[15] 廖晓昕.稳定性的理论、方法和应用[M] .武昌:华中科技大学出版社, 1999.LIAO Xiaoxin.T heory methods and application of stability[M] .Wuchang:Huazhong University of Science and Technology Press, 1999.

[16] 龚文振, 梁家荣.离散微分代数系统的有界性及周期解的存在性[J] .桂林工学院学报, 2005, 25(2):259.GONG Wenzhen, LIANG Jiarong.Boundary and existence of periodic solution to discrete differential algebraic systems[J] .Journal of Guilin University of Technology, 2005, 25(2):259.