密立根油滴实验数据处理的一种方法

刘海力，唐贤健，谢常清

（湖南人文科技学院，湖南娄底 417000）

密立根油滴实验数据处理的一种方法

刘海力，唐贤健，谢常清

（湖南人文科技学院，湖南娄底 417000）

以在重力场和静电场中运动的带电油滴为研究对象，提出了一种数据处理的方法，快速、准确地求解出基本电荷的电量，验证电荷的不连续性。

不连续性 ；密立根油滴；基本电荷

密立根油滴实验是实验物理学史上的经典实验，其构思巧妙，方法简便，结论正确，因而是目前高校理工科及物理专业必做的实验。但是，对油滴带电量数据的进一步处理方法确始终存在着重大缺陷［1］。现在，实验室一般采用“反向验证法”，即将测量和计算得到的一组油滴带电量q1，q2，…qi…qn分别除以基本电荷的理论值e＝1.602× 10-19C，把得到的商四舍五入取整，作为油滴所带基本电荷的个数ni，再用ni去除qi，得到的值即为实验测量的电子电荷值［2］。该方法操作简单，但是必须事先知道“电荷的不连续性”及“基本电荷的公认值”，而这两点正是本实验需要验证的内容，因而不符合物理实验数据处理的一般规则，缺乏科学性，这种通过结果求结果的数据处理方法，不利于培养学生对数据处理能力的训练。

因此，很多科研工作者根据自身实际情况，提出了数据处理的新方法［3－7］。本文根据我校实际情况，提出了一种数据处理的方法，快速、准确地求解出基本电荷的电量。

1 实验原理

用喷雾器将油滴喷入电容器两块水平的平行电极板之间时，油滴经喷射后，一般都是带电的。在不加电场的情况下，小油滴受重力作用而降落，当重力与空气的浮力和粘滞阻力平衡时，它便作匀速下降，它们之间的关系是：［8－9］

式中：m g为油滴受的重力；F1为空气的粘滞阻力，B为空气的浮力。

（6）式表明：按（3）式求出油滴的半径α后，由测定

当平行电极板间加上电场时，设油滴所带电量为q，它所受到的静电力为qE，E为平行极板间的电场强度，E＝U／d，U为两极板间的电势差，d为两板间的距离。适当选择电势差V的大小和方向，使油滴受到电场的作用向上运动，以vE表示上升的速度。当油滴匀速上升时，可得到如下关系式：

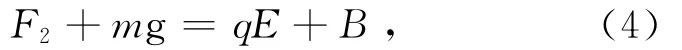
上式中F2为油滴上升速度为vE时空气的粘滞阻力：

由（1）、（4）式得到油滴所带电量q为的油滴不加电场时下降速度vg和加上电场时油滴匀速上升的速度vE，就可以求出所带的电量q。

由于斯托克斯定律对均匀介质才是正确的，对于半径小到10-6m的油滴小球，其大小接近空气空隙的大小，空气介质对油滴小球不能再认为是均匀的了，因而斯托克斯定律应该修正为

式中：b为一修正常数，取b＝6.17×10-6m· cm Hg；P为大气压强，单位是cm Hg。利用平衡条件和（4）式可得

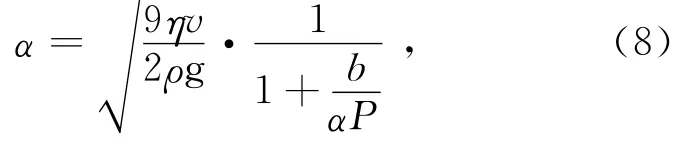
上式根号下虽然还包含油滴的半径α，因为它是处于修正项中，不需要十分精确，仍可用（6）式来表示。将（8）代入（4）式得：

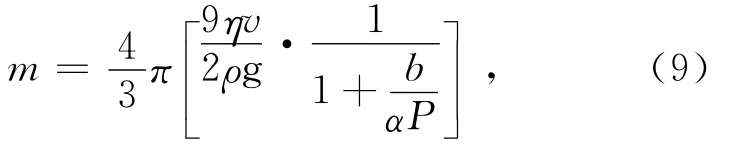
当平行极板间的电压为0时，设油滴匀速下降的距离为l，时间为t，则油滴匀速下降的速度为

将（10）式代入（9）式，再将（9）式代入（1）式得

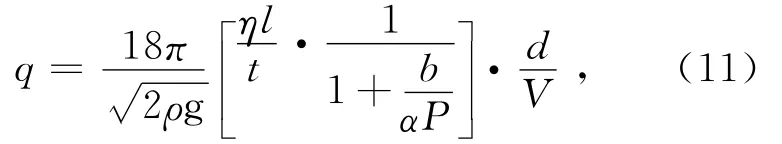
实验发现，对于同一个油滴，如果改变它所带的电量，则能够使油滴达到平衡的电压必须是某些特定的值Vn。研究这些电压变化的规律可以发现，他们都满足下面的方程

式中n＝±1，±2…，而e则是一个不变的值。

对于不同的油滴，可以证明有相同的规律，而且e值是相同的常数，这即是说电荷是不连续的，电荷存在着最小的电荷单位，也即是电子的电荷值e。于是，（12）式可化为

根据上式即可测出电子的电荷值e，验证电荷的不连续性。

2 实验仪器

实验的主要仪器有：主机、油滴盒、CCD成像系统、监视器等。

3 实验数据及处理

3.1 实验数据

经过测量，得出一组实验数据，见表1。

表1 密立根油滴实验数据

3.2 实验数据处理过程

通常情况下，数据处理时，采用“反向验证法”，处理情况见表2。

表2 利用“反向验证法”处理密立根油滴实验数据

这种方法操作简单，但是必须事先知道“电荷的不连续性”及“基本电荷的公认值”，而这两点正是本实验需要验证的内容，因而不符合物理实验数据处理的一般规则，缺乏科学性，这种通过结果求结果的数据处理方法，不利于培养学生对数据处理能力的训练。

因此，笔者利用matlab编写程序，计算出基本电荷量e的值，基本思路如下：

①选择油滴中电量最小的油滴，记下电量Qmin；

②每个电荷量Q分别对Qmin求余Rem；

③选择Rem与“Qmin－Rem”的较小值；

④每组较小值平方后求和RSS；

⑤分别用Qmin／2，Qmin／3…Qmin／m代替Qmin，重复②③④，直到Qmin／m＜1×（10-19C）；

⑥比较所有RSS值，输出RSS的最小值及最小值时的m值；

⑦用每组数据除以Qmin／m，依四舍五入求出基本电荷个数n；

⑧根据Q＝n＊e，用最小平方法拟合，求出e。

程序为：

4 结 论

本文以在重力场和静电场中运动的带电油滴为研究对象，利用matlab编写程序，快速、准确地求解出基本电荷的电量，验证电荷的不连续性，克服了“反向验证法”的缺点。

［1］ 李波欣.密立根油滴实验数据处理的新方法［J］.渤海大学学报：自然科学版，2005，26（4）：355-356.

［2］ 芦明霞，李斌，王天会，等.密立根油滴实验的几种数据处理方法的比较［J］.理工科研，2009，5：276.

［3］ 宋五洲.密立根油滴实验数据处理［J］.大学物理，2005，24（12）：57-62.

［4］ 丁红星，戴丽莉.密立根油滴实验数据处理方法的分析与改进［J］.大学物理，2005，24（7）：40-43.

［5］ 王广涛，陈健，魏建宇，等.密立根油滴实验数据的处理方法［J］.物理实验，2004，24（12）：22-24.

［6］ 罗春梅.密立根油滴实验数据的计算机处理［J］.物理与工程，2008，18（6）：28-29.

［7］ 吕承启，陈荣根.运用“图解法”进行密立根油滴实验的数据处理［J］.滁州师专学报，2000，2（2）：50，59.

［8］ 谢常清.基础物理实验［M］.长沙：中南大学出版社，2007.

［9］ 李强.大学物理实验［M］.成都：西南交通大学出版社，2010.

A Data-Processing Method for Millikan’s Oil-drop Experiment

LIU Hai-li，TANG Xian-jian，XIE Chang－qing

（Hunan Institute of Humanities，Hunan Loudi 417000）

This article investigated the moving charged droplets in gravity field and electrostatic field，proposed a data processing method，which can quickly and accurately calculate the elementary charge and verify the discontinuity of charge.

the discontinuity of charge；Millikan’s oil-drop experiment；elementary charge

O4-33

A

1007-2934（2011）06-0093-03

2011-09-09

湖南省教育厅教学改革研究立项项目（2007150）