谱约束下拟自反矩阵的最佳逼近问题

陈志宝,张忠志,雷秀仁

（1.华南理工大学数学系,中国广州 510640;2.东莞理工学院计算机学院,中国东莞 523808）

谱约束下拟自反矩阵的最佳逼近问题

陈志宝1＊,张忠志2,雷秀仁1

（1.华南理工大学数学系,中国广州 510640;2.东莞理工学院计算机学院,中国东莞 523808）

通过研究拟自反矩阵的逆特征值问题及其最佳逼近问题,建立了拟自反矩阵逆特征值问题有解的充要条件,得到了解的一般表达式.进一步,对于任意给定的n阶复矩阵,得到了相关最佳逼近问题解的表达式.

拟自反矩阵;逆特征值问题;最佳逼近;矩阵范数

在对电学、光学和自动控制的线性系统的检测和复原过程中,由于资料不全或者要求对已有数据进行校正的情况下,提出了谱约束条件下矩阵的最佳逼近问题[1-3].描述这种问题的数学模型如下∶

问题1给定X∈Cn×m,Λ=diagλ1,λ2,…λm∈Cm×m,求矩阵A∈S,使得

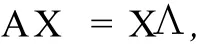
其中S为某一给定的矩阵集合.

问题2给定矩阵A＊∈Cn×n,,求矩阵^A∈SX,Λ,使得

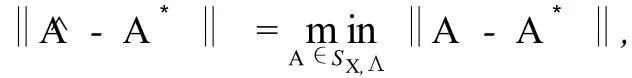
其中SX,Λ是问题1的解的集合.

针对不同的约束矩阵集合S,文献[4]研究了实对称矩阵的逆特征值问题与最佳逼近问题;文献[5]建立了埃尔密特广义汉密尔顿矩阵逆特征值问题可解的充分必要条件,并给出了相关最佳逼近问题解的显式表达式.由于自反矩阵与反自反矩阵、中心对称矩阵在物理学、信息论、线性系统理论、线性估计理论等领域有着重要的应用[6-8],上述矩阵有关问题的研究取得了一些成果.文献[9]研究了谱约束下反自反矩阵的最佳逼近问题,文献[10]研究了中心对称矩阵的一类反问题.本文中笔者将研究拟自反矩阵的逆特征值问题与最佳逼近问题.

定义1给定非奇异的Hermite矩阵P∈Cn×n,矩阵A∈Cn×n,若PA=AP,则称矩阵A是关于P的拟自反矩阵.

假定矩阵P不变,把所有的n×n拟自反矩阵组成的集合记为QCn×n,令问题1中的矩阵集合S=QCn×n,显然,QCn×n是Cn×n的一个线性子空间.当矩阵P为广义反射阵（即PH=P,P2=I）时,拟自反矩阵为自反矩阵,当P=（en,en-1,…,e1）（其中ei为n阶单位矩阵In的第i列i=1,2,…,n）时,拟自反矩阵为中心对称矩阵,因此,本文的研究涵盖了自反矩阵与中心对称矩阵的逆特征值问题.

为了讨论的方便,本文引入如下符号∶In为n阶单位阵;A+为矩阵A的Moore-Penrose广义逆;AH为矩阵A的共轭转置;tr（A）为矩阵A的迹;对A,B∈Cn×n,定义A,B的内积为由此内积导出范数为,这是Frobenius范数,且Cm×n构成一个完备的内积空间.

本文的结构如下∶在第2节,证明了拟自反矩阵的表示定理;在第3节,证明问题1有解的充分必要条件,并给出解的一般表达式;在第4节,证明问题2解的存在唯一性定理,并给出最佳逼近解的一般表达式.

1 拟自反矩阵的表示

本节讨论拟自反矩阵的一般表达式.首先给出如下引理.

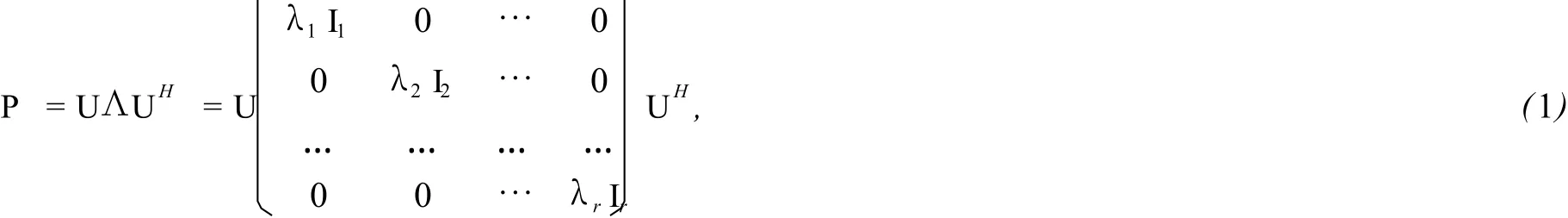
引理1[11]P∈Cn×n是非奇异的Hermite矩阵,则P的谱分解形式可表示成其中U是n×n酉矩阵,ui （i=1,2,…,n）表示U的第i列向量.λi （i=1,2,…,r）是矩阵P的互不相同的特征值,其重数分别

引理2A是拟自反矩阵的充要条件是∶

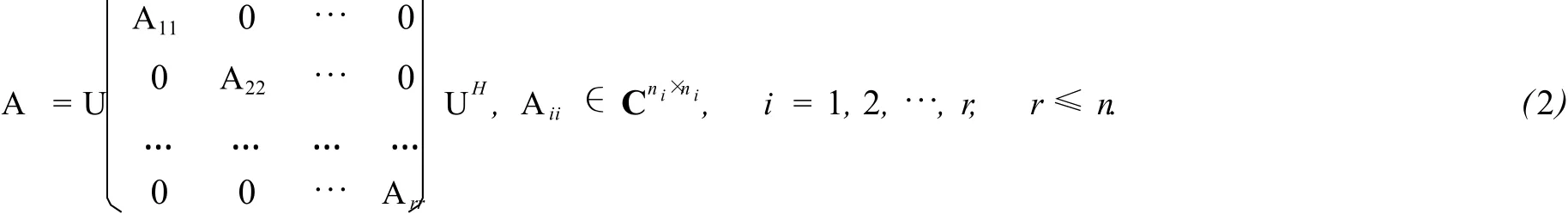
证显然,若式（2）成立,则由引理1容易验证PA=AP,即矩阵A是关于P的拟自反矩阵.若A是关于P的拟自反矩阵,由拟自反矩阵的定义和（1）式可知∶

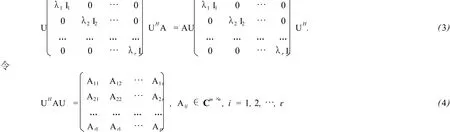
将式（4）代入式（3）并简化得λiAij -λjAij=0,因此,当i≠j时,有∶

将式（5）代入式（4）,并变形可得式（2）.

2 问题1的解

这一节,证明问题1的解存在的充要条件,并推导通解的一般表达式.首先,引入如下引理.

引理3[11]设X∈Cm×p,B∈Cn×p,则问题AX=B有解的充分必要条件是BX+X=B.并且有解时,通解可表示为A=BX+ +Z（I-XX+）,其中Z∈Cm×n.

定理1给定X=x1,x2,…,xm∈Cn×m,Λ=diagλ1,λ2,…λm∈Rm×m,令

则问题1在QCn×n中的充分必要条件是∶

因此,方程AX=XΛ同解于方程AiiXi=XiΛ,i=1,2,…,r.

由引理3知,方程AiiXi=XiΛ,i=1,2,…,r有解的充分必要条件是XiΛX+iXi=XiΛ（i=1,2,…,r.）且解的表达式为∶

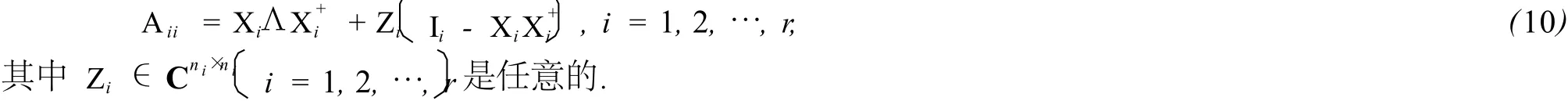
综上所述,（7）式是问题1有解的充分必要条件,且（7）式成立时,将（10）式代入到（9）式,可得问题1的一般解的表达式（8）.

3 问题2的解

在这一节,先证明问题2解的存在性与唯一性,然后推导其最佳逼近解的表达式.

[1] BARUCH M.Optimization procedure to correct stiffness and flexibility matrices using vibration tests[J].Aiaa J,1978,16: 1208-1210.

[2] BERMAN A,NAGY E J. Improvement of a large analyticalmodel using test data[J].Aiaa J,1983,21:1168-1173.

[3] JOSEPH K T.Inverse eigenvalue problem in structural design[J].Aiaa J,1992,10:2890-2896.

[4] 孙继广.实对称矩阵的两类逆特征值问题[J].计算数学,1988,1:282-290.

[5] ZHANG Z Z,HU X Y,ZHANGL.The solvability conditions for the inverse eigenvalue problem of Her mitian generalized Hamiltonian matrices[J].Inve Prob,2002,18（2）:1369-1376.

[6] ANDREW IJ.Centrosymmetric matrices[J].Siam Rev,1998,40（1）:697-698.

[7] 徐 仲,张凯院,陆 全.Toeplitz矩阵类的快速算法[M].西安:西北工业大学出版社,1999.

[8] CHEN H C.Generalized reflexivematrices:special properties and applications[J].Siam JMatrixAnalAppl,1998,19:140-153.

[9] 关 力,张忠志,谢东秀.谱约束下反自反矩阵的最佳逼近问题[J].数学物理学报,2009,29（2）:316-323.

[10] 周 硕,吴柏生.中心对称矩阵和反中心对称矩阵的一类反问题[J].高等学校计算数学学报,1988,3:282-290.

[11] 周树荃,戴 华.代数特征值反问题[M].郑州:河南科学技术出版社,1991.

Opt im alApprox im ation Problem of Q uasi-Reflexive Matrices under the SpectralRestriction

CHEN Zhi-bao1＊,ZHANG Zhong-zhi2,LEI X iu-ren1
（1.Department ofMathematics,South China University of Technology,Guangzhou 510640,China; 2.School of Computer,Dongguan University of Technology,Dongguan 523808,China）

The inverse eigenvalue problem of quasi-reflexive matrices and relevant optimal approximation problem are considered.Some necessary and sufficient conditions of the solvability for the inverse eigenvalue problem are given.A general representation of the solution is presented for solvable case.Further more,for any given complexmatrix of d imensionn,an expression of solution for its optimal approximation is presented.

quasi-reflexive matrix;inverse eigenvalue problem;opt imal approx imation;matrix nor m

O241.6

A

1000-2537（2011）02-0016-04

2010-10-28

国家自然科学基金资助项目（10571012）

＊通讯作者,E-mail:max_zbc@163.com

（编辑 沈小玲）