基于非信任光源的诱骗态量子密钥分发

陈明娟,刘 翔

（湖南师范大学物理与信息科学学院,中国长沙 410081）

基于非信任光源的诱骗态量子密钥分发

陈明娟,刘 翔＊

（湖南师范大学物理与信息科学学院,中国长沙 410081）

通过考虑Alice设备内部的统计波动,研究了弱真空诱骗态量子密钥分配方案中该统计波动对双向系统非信任源的密钥产生率和最大安全距离的影响.研究表明:该波动会在一定程度上降低密钥产生率和最大安全传输距离.

非信任源;统计波动;双向系统;弱真空诱骗态

量子密钥分配（quantum key distribution简称QKD）能在通信双方（Alice和Bob）之间建立无条件安全密钥,任何存在的窃听者将引入较高的量子比特错误率（QBER）而被通信双方发现.自BB84协议[1]提出以来, QKD得到了迅速的发展[2-4].然而,要想实现绝对安全的密钥分配方案,需要单光子源.但在现实中没有这样的单光子源,只有通过将相干光源衰减来近似获得单光子源,由于衰减后无法避免的存在多光子,通信容易受到PNS（Photon numbers splitting）攻击[5-7].对此,Hwang提出了一种可以有效的阻止PNS攻击的诱骗态方案[8],该诱骗态量子密钥分配方案[14-17]得到了广泛的应用,并已被证明是抵抗PNS攻击的最有效方法[9-13].本文从实际设备情况出发介绍应对PNS攻击的弱真空诱骗方案.采用双向传输Plug-and-play系统[18-23],由于该系统的源容易被窃听者控制,通常这种源被称之为非信任源[24-27],本文考虑了Alice实验设备内部的统计波动对弱真空诱骗方案最大安全传输距离和密钥产生率的影响,并与Alice实验内部无统计波动的结果进行了对比,发现这种波动确实会在一定程度上降低密钥产生率和最大安全传输距离.

1 模型与密钥产生率

在双向传输plug-and-play系统中,由于两路光子走的空间路径完全相同,可以自动补偿双折射效应和相位抖动,但是因为光子双向传输,使其容易受到木马攻击.如图1所示,源在Bob一端通过激光器发出光脉冲,经衰减通过光纤传入Alice处,窃听者在源进入Alice实验设备前可以完全控制源,掌握发送给Alice的脉冲光子数甚至是发出光脉冲取代原来的光脉冲.这样的攻击我们称之为木马攻击,源称之为非信任光源.源传入Alice后,Alice对脉冲进行探测和编码,把编码的脉冲发回给Bob.窃听者在位置1进行非破坏性测量知道发送给Alice的每个脉冲中的光子数,从而有利于它在位置2进行PNS攻击.对于非信任源的量子密钥分配方案的安全性已经被讨论[24-27].

诱骗态的核心思想是在考虑信号光源脉冲的计数率时,同时引入一组仅仅在强度上和信号光源不同的光源为诱骗光源,然后通过两种光源的总的计数率和量子比特错误率（QBER）来估计单光子态的计数率和QBER.在渐进极限情况下,当通信双方交换的脉冲长度N为无穷大时,弱诱骗方案被证明是最合理的方案[9].本文首次考虑了脉冲传入Alice内部后,实验设备内部的统计波动对弱诱骗方案传输的最大安全距离和密钥产生率的影响.在弱诱骗态量子分发实验中,Bob发出的信号包括三个态,信号态、诱骗态、真空态,信号态在Alice内部的传输率为λS,诱骗态在Alice内部的传输率为λD,真空态在Alice内部的传输率为0.由于实验中各种误差的存在,在设定Alice内部的传输率时,将无法避免内部的统计波动的影响.考虑Alice内部的统计波动其中λOS、λOD是最佳传输率,且满足λOS＞λOD.我们利用信号态来形成最终密钥,诱骗态用来探测信道.在实际的通信中,有两类比特信息∶一类是标记比特（多光子态）,这类比特是不安全的,攻击者可以在不引入误码率的同时截获信息;另一类是非标记比特（单光子态）,这类比特是安全的.对于进入Alice内部进行编码的光子数m∈[（1-δ）N,

（1+δ）N]是非标记比特,m＜（1-δ）N orm＞（1+δ）N是标记比特[28],不少于（1-Δ-ε）K的非标记比特具有较高的保真度,其中满足ε2K≫1,K是进入Alice内部编码的光脉冲[25].本文的研究主要是针对（1-Δ-ε）K的非标记比特.非标记比特的计数率和QBER的上下限分别为[25] ∶

当m（m∈[（1-δ）N,（1+δ）N]）个光子进入Alice实验设备内部,有n个光子从Alice内部发射出来的几率为[25] ∶

当考虑Alice设备内部统计波动时,pn （m）的上限和下限分别为∶

上式须满足λo （1+σ）N（1+δ）＜1,即输出的光子数要小于1.为了要得到最小的pn （m）的范围,δ、σ要尽可能的小,但是δ、σ变小会影响单光子计数率和QBER,所以,不同的设备要选择合适的δ、σ.

本文中诱骗态QKD都是基于Gottesman,Lo,Lutkenhaus和PreKill（GLLP）公式[3],GLLP证明了基于BB84协议的实际QKD系统,它的安全密钥产生率为[3]:

其中q的选择依赖于具体的密钥分配协议,对于BB84协议,Alice和Bob只有一半的几率选择了相同的基,故q=0.5.下标u表示信号光源的平均光子数,f（Eu）表示纠错码的纠缠效率,H2（x）表示二进制Shannon熵函数.

Alice发射出的每个信号比特的错误纠正为∶

2 数值模拟及讨论

对1 550 nm的商用单模光纤,衰减系数α为0.21 dB/km,信号脉冲在信道中的传输率为η=10-αl/10,l为信道的传输长度,ηBob是Bob的探测效率,edec表示一个光子错误到达探测器的概率,e0是背景噪声引起的错误,可以认为背景噪声是完全随机的,即e0=0.5.Y0是暗计数.在Goggy等的模拟中[29],取edec=0.033,ηBob= 0.045,Y0=1.7×10-6,本文的研究中也将利用这些参数.

图2给出了数据计算的结果.从图中可以看出,当σ=0即无统计波动时,最大安全传输距离为144 km,此时最大安全距离的λos=3.3×10-7和λod=1.0×10-8.当σ=0.05时,最大安全距离和密钥产生率都减小,最大安全距离的λos=3.4×10-7和λod=1.0×10-8.当统计波动增加到σ=0.1,最大安全距离将减少23 km,最大安全距离的λos=3.5×10-7和λod=1.0×10-8.很明显,安全密钥产生率和最大安全传输距离随着σ的增大而减小,即Alice内部的统计波动越大,那么最大安全距离就越小.

通过数值计算,挑选最佳的实验参数,选择强度和比例恰当的信号态和诱骗态,可以获得弱真空诱骗方案的最大安全距离.如果输入脉冲满足泊松分布的平均光子数为N,则输出信号满足泊松分布的平均光子数为Nλ,实验的结果完全由Alice设备内部的传输率决定,由于设备内部存在统计波动,需考虑统计波动的影响.在我们的模拟中,通过穷举搜索算法得到最佳的λs和λD.

在模拟中,采用信号光源下的计数率和QBER,其可以表示为∶

图3给出了当Alice内部的统计波动为σ=0.01,而δ取不同值时即源的不确定性对弱真空诱骗方案密钥产生率和安全传输距离的影响.由图可知,当δ=0.01时,最大安全距离为140 km,当δ=0.05时,安全距离减小了8 km,当δ=0.1时,最大安全距离减小了20 km.

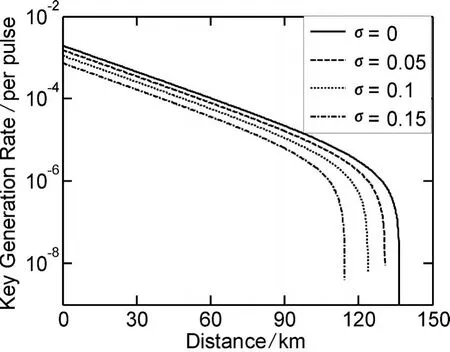
图2 统计波动对弱真空诱骗方案的密钥产生率和最大安全传输距离的影响

图3 源的不确定性对存在统计波动的弱真空诱骗方案的影响

图4展示了随着内部统计波动的逐渐增大,安全距离逐渐减小.由图可知,当σ＜0.2时,对安全传输距离的影响相对较弱,而当σ＞0.2时,安全距离随着σ的增大将急剧减小.当δ=0.01,σ＞0.255密钥将不可能安全传输,对于δ=0.05时,当σ＞0.222将不会实现安全传输.

3 结论

本文研究了Alice内部的统计波动对非信任源的弱真空诱骗态的影响.研究表明,当不计Alice的统计波动时,弱真空诱骗方案的最大安全距离可以达到144 km,而考虑Alice内部统计波动后,最大安全传输距离和密钥产率都在一定程度上减小了,且随着波动的增加,最大安全距离先缓慢减小,然后急剧减小.

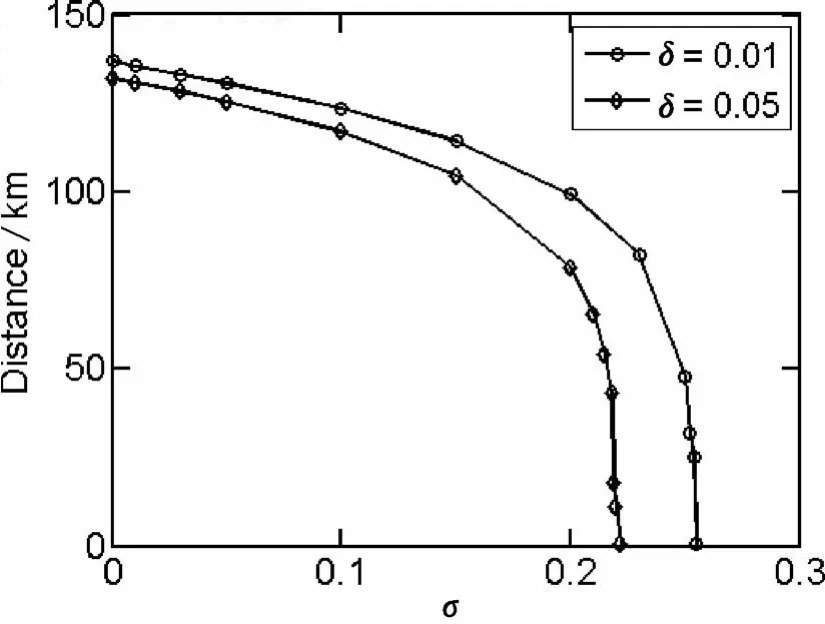
图4 弱诱真空骗方案选择不同的σ时对应的最大传输距离

[1] BENNETT C H,BRASSARD G.Quantum cryptography:public key distribution and coin tossing[C]//Proceedings of IEEE International Conference on Computers,Systems,and Signal Processing.New York:IEEE,1984.

[2] GU I Y Z,HAN Z F,MO X F,GUO G C.Exper imental quantum key distribution over 14.8 km in a special optical fibre[J]. Chin PhysLett,2003,20（5）:608-611.

[3] GOTTES MAN D,LO H K,LÜTKENHAUSN,et al.Security of quantum key distribution with imperfect devices[J].Quantum Inf Comput,2004（4）:325-328.

[4] PENG C Z,ZHANG J,YANGD.Experimental long-distance decoy-state quantum key distribution based on polarization encoding[J].Phys RevLett,2007,98（1）:10505.

[5] HUTTNER B,GIS IN N,MOR T.Quantum cryptographywith coherent states[J].Phys RevA,1995,51:1863-1867.

[6] LUTKENHAUS N,JAHMA M.Quantum key distribution with realistic states:photon-number statistics in the photon-number splitting attack[J].New J Phys,2002（4）:44-53.

[7] BRASSARD G,LUTKENHAUSN,MOR T,et al.Limitation on practical quantum cryptography[J].Phys RevLett,2000,85 （6）:1330-1333.

[8] HWANGW Y.Quantum key distribution with high loss:toward global secure communication[J].Phys Rev Lett,2003,91 （5）:57901.

[9] LO H K,MA X,CHEN K.Decoy state quantum key distribution[J].Phys RevLett,2005,94（23）:230504.

[10] LO H K.Quantum key distributionwith vacua or dim pulses as decoy state[C]//Proceedingsof IEEE International Symposium on Infor mation Theory.New York:IEEE,2004.

[11] MA X,Q IB,ZHAO Y,et al.Practical decoy state for quantum key distribution[J].Phys RevA,2005,72（1）:12326.

[12] WANG X B.Quantum error correction in spatially correlated quantum noise[J].Phys RevLett,2005,95:230503.

[13] WANG X B.Quantum key distribution with 4 intensities of coherent light[J].Phys RevA,2005,72（1）:12322.

[14] ZHAO Y,Q IB,MA X,et al.S imulation and implementation of decoy state quantum key distribution over 60km telecom fiber [C]//Proceedings of IEEE International Symposium of Infor mation Theory.New York:IEEE,2006.

[15] SCHM ITT-MANDERBACH T.Exper imental demonstration of free-space decoy-state quantum key distribution over 144 km [J].Phys RevLett,2007,98（1）:10504.

[16] PENG C Z,ZHANG J,YANGD,et al.Exper imental long-distance decoy-state quantum key distribution based on polarization encoding[J].Phys RevLett,2007,98（1）:10505.

[17] DYNES J F,YUAN ZL,SHARPE A W,et al.Practical quantum key distribution over 60 hours at an optical fiber distance of 20 km usingweak and vacuum decoy pulses for enhanced security[J].Opt Express,2007,15:8465-8467.

[18] MULLER A,HERZOG T,HUTTER B,et al.Plug and play systems for quantum cryptography[J].Appl PhysLett,1997,70 （7）:793-795.

[19] ZB INDEN H,GAUTIER J D,GIS IN N,et al.Interferometry with faraday mirrors for quantum cryptography[J].Electron Lett,1997,33:586-588.

[20] GIS IN N,R IBORDY G,TITTLR W,et al.Quantum cryptography[J].RevMod Phy,2002,74:145-195.

[21] GIS IN N,FASEL S,KRAUSB,et al.Trojan-horse attacks on quantum-key-distribution systems[J].Phy Rev A,2006,73 （2）:22320.

[22] ZHAO Y,Q IB,MA X,et al.Experimental quantum key distribution with decoy states[J].Phys Rev Lett,2006,96（7）: 705021-705024.

[23] SUN S H,MA H Q,HAN J J,et al.Quantum key distribution based on phase encoding in long-distance communication fiber [J].OptLett,2007,35:1203-1205.

[24] WANG X B,PENG C Z,ZHANG J,et al.General theory of decoy-state quantum cryptographywith source errors[J].Phys RevA,2008,77（4）:42311.

[25] ZHAO Y,Q IB,LO H K.Quantum key distribution with an unknown and untrusted source[J].Phys RevA,2008,77（5）: 52327.

[26] PENG X,J IANG H,XU B,et al.Experimental quantum-key distribution with an untrusted source[J].OptLett,2008,33: 2077-2079.

[27] PENG X,XU B,GOU.Passive-scheme analysis for solving the untrusted source problem in quatum key distribution[J].Phys RevA,2010,81（4）:42320.

[28] N IELSEN M A,CHUANG IL.Quantum computation and quantum information[M].Cambridge:CambridgeUniversity Press, 2000.

[29] GOBBY C,YUAN ZL,SH IELD A J.Quantum key distribution over 122 km of standard telecom fiber[J].Appl Phys Lett, 2004,84:3762.

Decoy State Q uantum Key D istribution w ith Untrusted Sources

CHEN M ing-juan,L IU X iang＊
（College of Physics and information Science,Hunan Nor malUniversity,Changsha 410081,China）

The security of the weak+vacuum decoy state protocolwith untrusted sources is studied,and the effects of internal statistic fluctuation on the final key rate and the transmittance distance are discussed.The results showed that both the maximum safe transmission distance and final key generation rates are reduced when the statistic fluctuation is considered.

untrusted sources;statistical fluctuation;two-way system;weak+vacuum decoy state

O432.2

A

1000-2537（2011）02-0025-05

2010-11-12

国家自然科学基金资助项目（11074072）

＊通讯作者,E-mail:liuxiang64@medmail.com.cn

（编辑 陈笑梅）