一类灰色随机多准则群决策方法
胡振华,杜 妮
(中南大学商学院,中国长沙 410083)
一类灰色随机多准则群决策方法
胡振华,杜 妮*
(中南大学商学院,中国长沙 410083)
针对准则值为区间灰数概率的离散型灰色随机变量且准则权重和决策者权重都完全未知的灰色随机多准则群决策问题,提出了一种基于偏差函数的决策方法.该方法通过计算每个决策者的主观判断矩阵与客观判断矩阵之间的偏差来确定该决策者的权重,基于主客观判断矩阵偏差最小化思想建立规划模型,求解该规划模型可同时得出准则权重向量和决策者权重向量,通过所求得的权重信息,分别得出在主、客观评价信息下的方案排序,综合这两种排序信息得出方案的最终排序.最后应用算例说明了该方法的合理性和有效性.
多准则群决策;灰色随机;区间灰数概率;偏差函数
对于庞大而复杂的决策问题,单个决策者难以做出完美的决策,这时就需要群体决策来解决这类问题.群体决策是把不同成员的关于方案集合中各方案的偏好按某种规则集结为决策群体的一致或妥协的群体偏好序[1].目前群决策的理论与方法已有很多,但是有关灰色随机多准则群决策的理论和方法还不多.文献[2]提出了风险型多准则群决策的一种与期望效用类似的线性集结方式进行个体偏好集结的方法;文献[3]给出了风险型多准则群决策的一种客观地计算专家权重和属性权重的方法;文献[4]提出了随机多准则群决策的一种不需决策者表明明示或暗示的偏好,而是通过搜索权重空间得出每个方案成为最优的信心指数和整体接受程度,通过这两个指标实现方案的排序的方法;文献[5]报道了随机多准则群决策的一种以互补判断矩阵表示各决策者的偏爱信息,将决策者模糊的随机偏爱信息进行量化的方法.以上4种方法有一个共同的不足之处,即对于某个准则的某个确定状态下的准则值是用实数来表示的,但在现实中由于各种不确定性很难给出实数的准则值,为了改进这个不足之处,文献[6]提出了灰色风险型多准则群决策的一种属性权重未知但决策者权重已知的,按每个方案相对于理想方案的优属度的大小进行方案排序的方法.但文献[6]中决策者权重是已知的,在现实中决策者的权重是很难事先确定的.因此本文探讨了一类准则值为区间灰数概率的离散型灰色随机变量,准则权重和决策者权重都完全未知的灰色随机多准则群决策问题.
1 问题描述

2 决策方法
2.1 数据处理

2.2 决策者权重和准则权重的确定
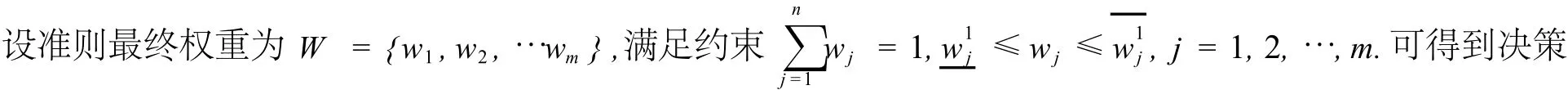

2.3 确定方案的排序
根据模型(p1)求得的准则权重和决策者权重设准则,可求出方案ai的客观综合评价值和主观综合评价值.其中方案ai的客观综合评价值为对方案的客观综合评价值按照定义3进行排序,得到整个方案集在客观评价信息下的排序,方案ai的客观排序数为ki (排在第一位的方案的客观排序数为1,依次给定所有方案的客观排序数).而方案ai的主观综合评价值为理得到整个方案集在主评价信息下的排序,可得方案ai的主观排序数为oi.方案ai的综合排序数为∶

其中α,β分别代表对客、主观信息的信任程度,因为主观偏好信息比较笼统和不精确,因此β应取较小的值,一般建议的取值为α=0.8,β=0.2.α,β的值取定后,即可得到每个方案ai的综合排序数ui.根据每个方案ai的客观排序数ki,主观排序数oi和综合排序数ui,参考文献[11]的排序思想,可得本文的排序规则∶
(1)ui小的方案ai为先;
(2)两个方案ai和aj的综合排序数那么方案ai优于方案aj ;(3)两个方案ai和aj的综合排序数若ki <kj,那么方案ai优于方案aj.
3 实例分析
企业计划开发一新产品,现有3种方案(a1,a2,a3)可供选择,考虑了3个指标,分别为经济效益c1,社会效益c2和污染损失c3(准则权重的约束为预测经济效益有很好(θ1)、好(θ2)、一般(θ3)和差(θ4)4种自然状态,社会效益和污染损失有很好(θ1)、好(θ2)和一般(θ3)3种自然状态,各自然状态发生的概率用区间概率表示.3位决策者es (s=1,2,3)分别对每个方案给出的客观评价数据(见表1~3)和主观偏好(见表4),对每个准则打分(见表5),求最优方案.

表1 决策者e1的客观评价表

表2 决策者e2的客观评价表

表3 决策者e3的客观评价表

表4 决策者的主观偏好
(1)用计算公式(1)把表1~3转化为无风险决策矩阵,再利用公式(2)和(3)进行规范化处理后得规范化无风险决策矩阵Ys (s=1,2,3).
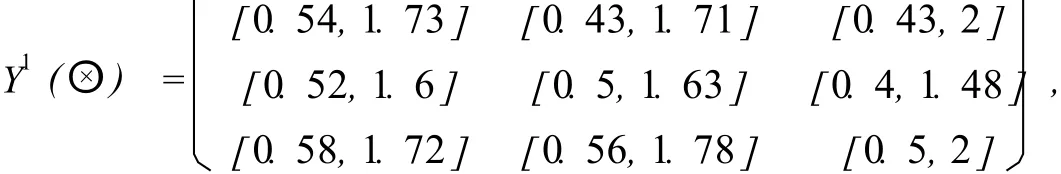

(2)根据上面的数据信息,可以构造出三位决策者的主、客观判断矩阵,然后通过MATLAB求解规划模型(p1)可计算出准则最终权重为∶W1=0.23,W2=0.64,W3=0.13;决策者权重为∶λ1=0.37,λ2=0.32,λ3=0.31.
(3)根据已求得的准则最终权重和决策者权重,求得各方案的客观综合评价值和主观综合评价值分别为∶
z1=[0.45,1.74],v1=[0.40,0.64];z2=[0.47,1.65],v2=[0.49,0.62];z3=[0.53,1.84],v3= [0.36,0.49].根据定义3可知z3>z1>z2;v2>v1>v3.根据公式(4)(取定α=0.8,β=0.2),可求出各方案的综合排序数为∶u1=2.6,u2=2.0,u3=1.4;因为u3<u2<u1,所以只需通过排序规则(1),即可得出a3>a2>a1的结论.
4 结束语
本文在考虑各状态的概率时,允许不同方案在各状态下的概率可以不同,这与现实更加相符.只需求解一个规划模型就可求得准则权重和决策者权重,为权重未知且具有方案偏好信息的灰色随机多准则群决策提供了一个比较简便方法,而且与其他的具有方案偏好信息的决策方法不同,一般的具有方案偏好信息的决策方法只在求解权重时用到方案偏好信息,在最后的综合评价时往往就不考虑这部分信息了,本文在综合评价时就考虑了这部分信息,使得方案的排序更加合理.
[1] HWANG C L,L IN M L.Group decision making under multiple criteria:method and application[M].Berlin:springer-verlag, 1987.
[2] 毕文杰,陈晓红.基于目标的风险型多属性群决策方法研究[J].统计与信息论坛,2009,24(3):8-12.
[3] 刘 宁,戴大双.BOT项目风险多属性群决策识别方法[J].技术经济,2009,28(9):50-52.
[4] LAHDELMA R,SALM INEN P.S MAA-2:stochastic multicriteria acceptability analysis for group decision making[J].Operations Research,2001,49(3):444-454.
[5] 刘 伟,陈内萍.基于互补矩阵的随机偏爱群体决策方法及应用研究[J].湖南师范大学自然科学学报,2009,32(4):27-31.
[6] 罗 党,周 玲,罗迪新.灰色风险型多属性群决策方法[J].系统工程与电子技术,2008,30(9):1674-1678.
[7] 刘思峰,郭天榜,党耀国.灰色系统理论及其应用[M].北京:科学出版社,1999.
[8] 徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2004.
[9] L IA GD,DA ISUKE Y,MASATAKE N.A grey-based decision-making approach to the supplier selection problem[J].Math ComputMod,2007,46(3):573-581.
[10] 周宏安,刘三阳,李炳杰.基于目标规划和相对优势度的区间数互反判断矩阵排序法[J].数学的认识和实践,2006, 36(6):63-67.
[11] 陈明琴,何湘潘.二维足码选择定位法:一种新的群决策方法[J].系统工程理论与实践,1997(2):18-22.
A Glass of Grey Stochastic Multi-criteria Group Decision-Making Approach
HU Zhen-hua,DU N i*
(School ofBusiness,Central South University,Changsha 410083,China)
For grey stochastic multi-criteria group decision-making problem,in which criteria value is discrete grey stochastic variable with interval grey number probability and weight is unknown,one decision-making approach based on deviation function is given.In this approach,the weight of decision-makerswas determined by calculating the deviation of each decision-maker's subjective and objective judgmentmatrix,and programmingmodelwas established based on the thought ofmin imizing the deviation of the subjective and objective judgmentmatrix.By solving it,both the weight vector of criteria and the weight vector of decision-makers can be obtained.By the weight information one ranking of the alternatives based on subjective evaluation infor mation and the other ranking of the alternatives based on objective evaluation information were calculated,and the final ranking of the alternatives was obtained by combination of these two ranking infor mation.Finally,the feasibility and validity of this approach are demonstrated by an example.
multi-criteria decision-making;grey stochastic;interval grey numberprobability;deviation function
O211.9
A
1000-2537(2011)02-0020-05
2011-03-06
国家自然科学基金资助项目(71072079)
*通讯作者,E-mail:dudu2730@hotmail.com
(编辑 陈笑梅)

