用相对Gibbs自由能方法计算羧酸的pKa值

何建军,陈香兰,曾 跃＊

（1.湖南交通工程职业技术学院,中国衡阳 421001;2.湖南师范大学化学化工学院,中国长沙 410081）

用相对Gibbs自由能方法计算羧酸的pKa值

何建军1,陈香兰2,曾 跃2＊

（1.湖南交通工程职业技术学院,中国衡阳 421001;2.湖南师范大学化学化工学院,中国长沙 410081）

运用密度泛函方法以及连续极化溶剂模型（PCM）,在B3LYP/6-31+G（d,p）水平上计算了86种羧酸在水溶液中的97个pKa值.在本文pKa值的计算中,用羧酸在水溶液中的电离反应直接计算羧酸电离Gibbs自由能,并用相对Gibbs自由能来计算羧酸的pKa值.结果表明,计算值能很好地与实验值吻合,其标准偏差为±0.36 pKa单位.

密度泛函理论;羧酸;连续极化模型

有机羧酸类化合物的pKa值是有机羧酸类化合物的重要特性参数之一,尽管常见有机羧酸类化合物的pKa值可以通过实验确定或从相关手册上查到,但对于有些物质,如一些反应中间体,其pKa值却无法用实验方法准确测量和从相关手册上查到.不仅如此,在某些情况下,实验测定值还存在较大不确定性.因此,人们长期致力于用各种各样的理论方法,如用从头算、密度泛函、分子建模等方法计算pKa值的大小.

在早期的研究中,大多数采用如（1）式所示的羧酸（HA）电离方程式从理论上计算pKa值[1]:

由于H+（aq）离子是无电子粒子,无法从理论上计算其Gibbs自由能G（H+（aq））,所以要使用（2）式计算其pKa值,需要使用G（H+（aq））的实验值.为了不使用G（H+（aq））的实验值,而是纯理论计算其pKa值,后来有人提出用羧酸电离方程式（3）来计算其pKa值[2]:

然而,计算结果表明,无论用式（2）或式（4）计算有机羧酸的pKa值,都存在有无法忍受的系统误差.

正因为如此,在前人的研究中,为了降低计算误差,pKa值的计算一般都是利用如下热力学循环间接计算电离反应的Gibbs自由能进而计算pKa值[3]:

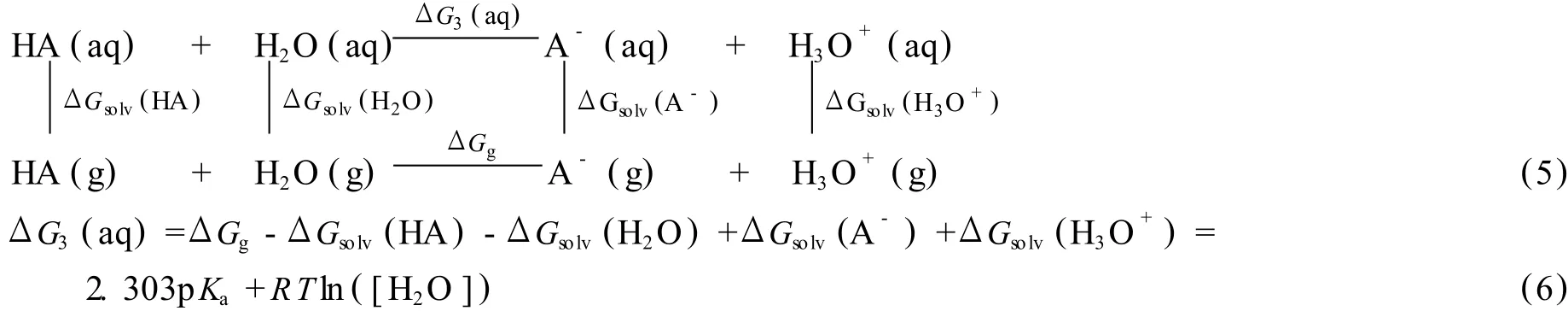
到目前为止,文献上几乎所有有关pKa值的计算的论文,都是采用该热力学循环或类似循环进行.尽管使用该循环计算pKa值的精度得到了较大的改善,但很大程度上增加了计算的工作量.

本文主要是运用密度泛函理论以及连续极化溶剂模型（PCM）,在B3LYP/6-31+G（d,p）水平上计算了86种羧酸在水溶液中的97个电离反应的Gibbs自由能改变（ΔG）,并用其相对Gibbs自由能来计算羧酸的pKa值.

1 理论和计算方法

1.1 pKa计算的热力学

从原理上讲,使用方程式（2）、（4）或（6）都可以计算羧酸的pKa值.然而它们或多或少存在不足.例如,对于方程式（2）,正如前面所提及的,主要困难是不能从理论上实现自由质子Gibbs自由能的计算.而对于方程（4）和（6）,由于H2O（aq）和H3O+（aq）的Gibbs自由能的计算存在较大误差,这导致pKa值的计算精度受到较大影响.很明显,在pKa值计算方法的设计中,水合质子的选择会直接影响计算的精确度.Newton等的从头算研究表明,使用水合质子,其结构和光谱特性与实验值十分吻合[4].因此比H3O+能更好地代表水合质子.据此,我们选择H9O+4代表水合质子来进行羧酸pKa值的计算,即使用方程式（7）来计算羧酸pKa值:

使用（7）式计算羧酸的pKa值,发现仍然存在较大的系统误差.为了减少计算误差,选取一种已知pKa值的羧酸作为标准参照物.假设该标准参照物的pKa值为pKa（s）,根据（8）式得:

将（9）式与（8）式两边相除并整理得:

由于[H2O]=55.56 mol·L-1,并令ΔG/ΔG（s）=ΔGr,即任意羧酸与参照羧酸的相对电离Gibbs自由能,则:

这样,通过选取适当的标准参照羧酸,利用式（11）即可获得较高精度的pKa计算值.

1.2 电离Gibbs自由能ΔG的密度泛函计算

在本研究中,使用密度泛函理论（DFT）,在B3LYP/6-31+G（d,p）水平[5]上对相关物质（HA,A-,H2O和H9O+4）进行几何全优化后再对其进行Gibbs自由能的计算,最后用（8）式计算羧酸的电离Gibbs自由能变化ΔG.在计算中,使用连续极化模型（PCM）模拟水溶液的溶剂化效应[6].本研究所有计算均采用Gaussian-03[7]软件完成.

2 结果与讨论

表1是86种常见羧酸（其中75种一元酸,11种二元酸）的97个pKa值的实验值与计算值之间的比较.

从表1不难看出,使用方程式（8）所计算出的pKa值（即pKa（calc.））与实验值pKa（exp.）相比,有很大误差,其计算偏差ΔpKa[pKa（calc.）-pKa（exp.）]的标准偏差S为12.03,其中最大偏差为15.21,已经达到了无法忍受的程度.这是由于连续极化溶剂模型（PCM）忽略了第一溶剂化层强的氢键作用[8],因而导致计算水溶液中羧酸及其电离物等的Gibbs自由能时,存在较大的系统误差.

为了降低由于Gibbs自由能计算的系统误差对pKa值计算精度的影响,选择2,4,6-三硝基苯甲酸（2,4, 6-（NO2）3C6H2COOH）作为计算pKa值的标准参照物,用方程式（11）计算了常见羧酸的97个pKa值,结果列于表1中.从表1中不难看出,使用本文提出的相对Gibbs自由能的方法计算常见羧酸的pKa值,准确度较高,其标准偏差S为0.36,最大ΔpKa为0.89,达到较为满意的程度.

表1 本工作中研究的羧酸及其pKa值

续表

续表

3 结论

本研究以2,4,6-三硝基苯甲酸（2,4,6-（NO2）3C6H2COOH）作为标准参照物,用密度泛函理论和连续溶剂化模型计算了86种常见羧酸在水溶液中的97个电离反应的相对Gibbs自由能,并根据相对Gibbs自由能计算了这86种羧酸所对应的97个pKa值,结果表明:

（1）直接使用羧酸电离反应计算羧酸的电离Gibbs自由能,并通过Gibbs自由能计算羧酸的pKa值的方法,存在极大的系统误差.但使用相对Gibbs自由能的方法,计算羧酸的pKa值则可以很大程度降低pKa值计算误差.该方法是直接使用羧酸电离反应计算羧酸的pKa值,而不像以前人们所提出的方法那样,需要通过设计热力学循环间接计算电离反应的ΔG进而计算出pKa.

（2）选择2,4,6-三硝基苯甲酸（2,4,6-（NO2）3C6H2COOH）作为计算pKa值的标准参照物,使用相对Gibbs自由能的方法计算了常见羧酸的97个pKa值,与实验值相比较,其标准偏差为0.36,最大偏差为0.89.

因此,用相对Gibbs自由能计算常见羧酸的pKa值是一个简单且行之有效的计算方法.

[1] L IM C,BASHFORD D,KARPLUSM.Absolute pKacalculationswith continuum dielectric methods[J].J Phys Chem,1991, 95（14）:5610-5620.

[2] SCHUURMANN G,COSSIM,BARONE V,et al.Prediction of the pKaof carboxylic acids using the ab initio continuum-solvation model PCM-UAHF[J].J Phys Chem A,1998,102（33）:6706-6712.

[3] TUNON I,S ILLA E,TOMASIJ.Methylamines basicity calculations:in vacuo and in solution comparative analysis[J].J Phys Chem,1992,96（22）:9043-9048.

[4] NEWTON M D,EHRENSON S.Ab initio studies on the structures and energetics of inner-and outer-shell hydrates of the proton and the hydroxide ion[J].J Am Chem Soc,1971,93（20）:4971-4990.

[5] BECKA D.Density functional thermochem.Ⅲ.The role of exact exchange[J].J Chem Phys,1993,98:5648-5653.

[6] BARONEV,COSSIM.Quantum calculation ofmolecular energies and energy gradients in solution by a conductor solventmodel [J].J Phys Chem A,1998,102（11）:1995-2001.

[7] FR ISCH M J,TRUCKS GW,SCHLEGEL H B,et al.Gaussian 03,Revision E.01[CP].Gaussian,Inc.,Wallingford CT, 2004.

[8] MUJ IKA J I,MERCERO J M,LOPEZ X.A theoretical evaluation of the pKafor twisted amides using density functional theory and dielectric continuum methods[J].J Phys Chem A,2003,107（31）:6099-6107.

[9] NAMAZ IAN M,HALVAN I S.Calculations of pKavalues of carboxylic acids in aqueous solution using density functional theory [J].J Chem Thermodyn,2006,38（12）:1495-1502.

[10] LYDE D R,Ed.,CRC Handbook of chemistry and physics[M].82nd ed.New York:CRC Press,2001.

[11] BROWN HC,BRAUDE E A,NACHOD F C.Deter mination of organic structures by physicalmethods[M].New York:Academic Press,1955.

Calculation on pKaValues of Carboxylic Acids in Aqueous Solution U sing Relative Gibbs Free Energy

HE Jian-jun1,CHEN X iang-lan2,ZENG Yue2＊
（1.Hunan Technical College of Communications and Engineering,Hengyang 421001,China;
2.College of Chemistry and Chemical Engineering,Hunan Nor malUniversity,Changsha 410081,China）

The 97 pKavalues of 86 carboxylic acids in aqueous solution were calculated with density functional theorymethod at the level ofB3LYP/6-31+G（d,p）and the polarizable continuum model（PCM）was used to describe the solvent.The pKavalueswere directly calculated employing the relative Gibbs free energies of the carboxylic acid dissociations in aqueous solution.In thiswaywe obtained an approach inwhich pKavaluesof carboxylic acids in aqueous solution can be predicted with the standard deviation of 0.36 in pKaunit.

density functional theory;carboxylic acids;polarizable continuum model

O641.12+1

A

1000-2537（2011）02-0048-06

2010-12-10

国家自然科学基金资助项目（21075037）

＊通讯作者,E-mail:zeng_yue@126.com

（编辑 杨春明）