弹载捷联惯导空中传递对准中火控匹配信息精度研究＊

鲁 浩，位晓峰，徐剑芸，程海彬，孟俊芳

（中国空空导弹研究院，河南洛阳 471009）

0 引言

对准问题是任何惯性导航系统在进行导航解算之前必须首先解决的关键技术之一，机载战术导弹惯导系统的传递对准是导弹空中发射前必须完成的关键过程[1]。弹载捷联惯导系统的初始对准采用动基座传递对准，机载火控系统通过接收机载主惯导系统信息，不间断地进行导弹飞行任务的计算，通过总线（1553B或429）将所需的空中传递对准信息实时传递给导弹捷联惯导，导弹捷联惯导利用卡尔曼滤波算法完成传递对准。机载火控系统是沟通机载惯导系统和导弹惯导系统的“桥梁”，是完成传递对准匹配信息“加工、处理与传输”的中枢。

从检索的文献来看，专题研究传递对准算法的文章很多，但涉及与传递对准机载火控匹配信息精度的研究很少。文中对载机主惯导传递的对准匹配信息精度进行了研究，分析了火控信息的更新周期、信息延迟时间误差以及信息精度对传递对准的影响。

1 机载火控系统的功能与作用

机载战术导弹武器系统主要包括：机载雷达、敌我识别系统、惯性导航系统、大气数据计算机、无线电指令系统、红外和光学瞄准系统、火控系统和发控装置等。其中机载火控系统是整个武器系统的控制与信息处理中枢，通过接收其它分系统的信息，为空空导弹提供飞行任务信息和控制指令，这其中包含了传递对准所需的各种信息。

从机载惯导系统的工作原理可以看出，主惯导系统能够精确地给出飞机相对于地球的准确位置、速度和姿态角信息等，采用“绝对导航”。“绝对导航”关注宏观精度，其导航输出信息的精度主要考虑“长周期”的要求，飞行时间可达数小时，惯导系统各项导航误差参数都是呈现长周期（舒拉周期84.4min）的振荡变化特性。

弹载惯导系统强调的是一次历经性的过程，具有“短周期”的特性（飞行时间最长200s），关注“微观”一次历经性连续过程的特性，表示速度的单位为m／s，不能忽略小数点后2～4位的数据。

“相对导航”是在建立机载火控基准导航坐标系的时刻，“冻结”机载惯导系统以前产生的导航误差，建立的机载火控基准导航坐标系导航参数的误差从“冻结”时刻起重新开始计算。

选用“相对导航”还是“绝对导航”，取决火控系统在进行传递对准匹配信息时采用了主惯导系统纯惯性导航参数还是INS／GPS组合导航参数。

对于机载导弹而言，因为其制导信息主要考虑飞机、导弹和目标之间的相对运动关系，采用了主惯导纯惯性的导航参数，因此选用“相对导航”。

2 火控匹配信息流的确定

机载平台式惯导系统的导航坐标系已经选用了游离方位坐标系，而且与大气机和GPS进行了组合。因此，机载平台式惯性导航系统输出的导航参数已不是纯惯性的，机载惯导的导航信息不能在机载导弹传递对准中直接采用，只能利用载机火控系统对主惯导的导航参数进行处理，在火控系统中重新构建机载导弹所需的导航系，该坐标系称为整个导弹武器系统的导航坐标系。导弹惯导系统的传递对准所需的各种基准信息和导弹中制导所需的目标信息都是从这个导航坐标系统中给出的。

用于空空导弹传递对准的匹配信息主要有两种：速度信息和姿态信息。

2.1 速度信息

“速度匹配”方案的主要优点在于：由于地球重力加速度的作用，水平失准角可以得到有效的估计，由比力形成的支撑矢量的长度随时间增长，可以有效地改善滤波算法中的信噪比。但方位通道需要通过陀螺罗经化（gyro compassing）把航向误差变换成速度误差来完成。因此传递对准过程中需要载机做具有水平加速度输出的机动飞行。

2.2 姿态四元数

采用姿态四元数信息作为传递对准的匹配信息，可以使传递对准的匹配信息中增加与角运动有关信息。采用 “速度＋姿态”匹配方案，再加以适当的机动，使传递对准状态方程的可观测性大大增加，从而使传递对准的速度和精度在“理论”上都得到提高。但采用姿态四元数信息作为传递对准的量测信息有很多缺点，将会大大增加滤波算法的复杂性，而且仅在载机的某些运动的情况下采用姿态四元数信息才会对传递对准的精度有明显的改善，这些缺点严重制约了姿态四元数信息在传递对准中的应用。

2.3 火控系统传递所需信息流

与传递对准有关的火控信息流如图1所示。

图1 传递对准有关的信息流

主惯导输出的导航信息包括：飞机姿态角ψ、θ、γ；飞机位置λ、φ、H；飞机地速VN、VU、VE；比力fpx、fpy、fpz；信息延迟时间τ1；平台的角速度矢量ωpx、ωpy、ωpz；游动方位角α等。

火控输出的传递对准信息包括：姿态四元数qib；飞机位置x、y、z；飞机惯性速度Vx、Vy、Vz；信息延迟时间τ2；重力加速度gx、gy、gz；杆臂长度 Rx、Ry、Rz等。

3 火控信息的建立过程

通常情况下，机载导弹选用惯性坐标系作为导航坐标系。导弹惯导系统的传递对准所需的各种基准信息和导弹中制导所需的目标信息都是从这个惯性坐标系统中给出的。

3.1 火控基准惯性坐标系[2]

火控导航惯性系是机载火控系统在机载导弹惯导系统传递对准开始之前的某一时刻（t＝0）建立的，此时，火控导航惯性坐标系与主惯导系统在t＝0时刻模拟的地理坐标系重合。模拟地理系与平台惯导系统的平台系在方位上相差一个游移方位角α。火控系统利用机载平台式惯导系统模拟这个地理系。此时，平台系与当地地理坐标系之间的转移矩阵为：

以后，在每一个计算周期T上，有：

式中：T为计算周期，（ωpxωpyωpz）T为平台惯导系统中平台系的指令角速度矢量。

3.2 姿态四元数

在火控系统建立姿态四元数信息时，首先计算机体系至平台系的转移矩阵，它与载机相对于当地地理系的姿态角以及平台的游移角有关。其次计算弹体系相对于机体系的安装矩阵，它与导弹在载机上的挂弹方式及机翼静态挠曲变形角度有关。则弹体系至导航系的转移矩阵为

四元数qib表示为：qib＝qip·qpB·qBb

式中 ：qib为弹体系b与惯性坐标系i的转换四元数；qip为惯性系i与平台系p之间的转换四元数；qpB为平台系p与机体系B之间的转换四元数；qBb为机体系B与弹体系b之间的转换四元数。qib的精度取决于弹体的安装几何误差、载机惯导系统的姿态误差，特别是机翼变形的补偿精度。

3.3 载机惯性速度[4]

采用“相对导航”的设计概念，在火控导航坐标系建立的时刻（t＝0），记忆下平台惯导系统在t时刻的速度（即北向速度VN、天向速度VU与东向速度VE），此时火控起始时间为零。

计算在每一个计算步长T上，沿平台坐标系轴向的比力值，可得：

在惯性系比力速度增量的计算：

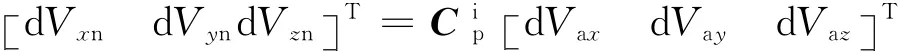
在惯性坐标系中火控惯性速度的计算：

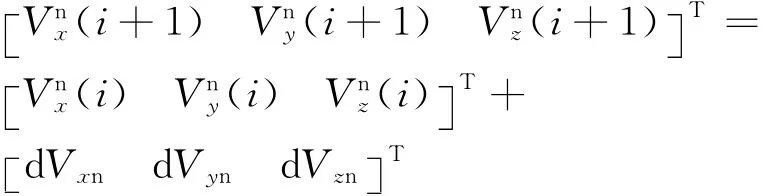
3.4 重力加速度

重力加速度在平台坐标系轴上的投影：

重力加速度在惯性坐标系上的投影：

4 火控匹配信息精度研究

机载火控系统提供的对准匹配信息精度应满足机载导弹捷联惯导对准精度要求。本节在“速度＋姿态”匹配方案条件下，采用逆向推理的方法，从导弹惯导对火控系统的信息要求出发，溯源到对火控系统匹配信息的精度要求。

4.1 速度信息精度研究[3]

在选用“速度”匹配传递对准算法时，为满足传递对准的精度要求，火控传递的速度精度误差必须满足下列公式：

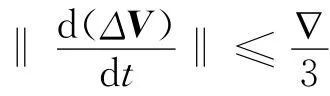
式中：ΔV为火控系统惯性速度的误差；∇为导弹惯导系统加速度计零位偏置。

目前国外载机均采用0.2～1nm／h以内的惯导系统，其陀螺漂移精度已达到0.03°／h以内，加速度计的零位偏置1×10－5g，在火控导航坐标系保持的有效时间内（暂定10min），坐标系的姿态角漂移仅为0.005°，速度的误差梯度仅为1×10－5g，这样的机载惯导系统的精度对空空导弹的影响很小，可以忽略。

重力加速度的计算精度应高于导弹加速度计的零位偏置，如果空空导弹加速度计的零位偏置为5×10－4g，则重力加速度的计算精度应为δg ＜5×10－4g。

4.2 姿态四元数的精度研究

姿态四元数Cib的精度取决于载机惯导系统的姿态误差、弹体的安装几何误差，特别是机翼变形的补偿精度。机翼是一个挠性体，机翼的变形含有准静态挠曲和高频振动。准静态挠曲是飞机机动及武器投放的载荷变化所引起的低频机翼弯曲。高频振动是由于大气湍流引起的结构振动。机翼弹性变形有弯曲变形和扭转变形两种，由于现代战机大都采用三角翼，因而扭转变形可忽略不计，只计算弯曲变形。

为了满足误差状态方程的小角度假设要求，由火控系统传递给导弹惯导系统姿态四元数的精度初步定为：滚动角20′～40′（1σ）；俯仰角15′～30′（1σ）；方位角10′～20′（1σ）。

4.3 信息同步时间延迟的精度研究

一般而言，飞机惯导系统的导航参数通过1553B总线（或429总线）传递给火控系统，火控系统处理完这些信息后，再通过1553B总线（或429总线）传递给导弹惯导系统。传递对准过程中信息传输时延是不可避免的。数据传输时延是影响传递对准精度的主要误差源之一，10ms的信息时间延迟，可导致几个mrad的姿态估计误差。依据实际工程的分析，从主惯导生成导航信息到导弹惯导接收到对准信息，在时间上大约延迟了40～120ms。因此，必须对主、子惯导的数据进行时间同步，数据同步的时延误差会引起同步精度变差，对对准的影响程度取决于机动大小。在下一节中，将通过仿真进行讨论。

4.4 信息传输频率研究

传递对准匹配信息的频率取决于火控系统传递对准信息的频率，假设飞机的飞行加速度是固定的，可以用两个火控传输值准确的计算出匹配速度值。当飞机的飞行加速度交变时，就不可能准确的得到主惯导的速度值。研究表明 “火控信息”的输入频率为8～10Hz，就可以满足传递对准对“火控信息”输入频率的要求，进一步提高输入频率不会明显地提高对准的精度，相反会增大对准过程的计算量。如果“火控信息”输入频率降低到1～2Hz，尤其是降低速度匹配参数的输入频率将会引起对准精度变差。因此，较快的测量频率（8～10Hz），有助于提高传递对准的快速性和精度。

5 仿真结果及分析

本节采用 Monte－Karlo方法进行仿真[5]，在仿真中，主要为了研究火控匹配信息更新周期、信息延迟时间误差对传递对准的影响，因而没有考虑机翼挠性变形、振动等的影响。为了有效减小卡尔曼滤波器的阶数，同时又能继承速度积分匹配法和位置匹配的优点，对准算法选用了新颖的 “平均速度”匹配方法。

5.1 仿真条件

进行50s的传递对准仿真，仿真条件见表1。数据传输时延最大90ms，最小20ms，采用一次插值法。实际失准角（安装误差角）依次设置为：Φx（0）：40′，Φy（0）：70′，Φz（0）：30′。

表1 仿真条件

5.2 信息更新周期对传递对准精度影响

由于篇幅所限，仅列出在水平直线飞行条件下的仿真图（图2～图4，以下同）。

由图2可以看出，随着信息更新频率减小，对准收敛的时间增长，失准角估计精度变差。在水平转弯飞行的条件下，也可以得出相同的结果。从图中可以看出，信息更新频率位于8～10Hz，失准角估计精度和对准收敛的快速性已满足战术武器要求。信息更新频率太快会增大滤波器的计算量，信息更新频率太慢会降低失准角的估计精度和对准收敛的快速性。在实际的工程应用中，火控信息的更新频率可以选在10Hz左右，此时对准收敛的快速性和精度都能满足要求且计算量适中。

图2 信息更新频率仿真结果

5.3 信息延迟误差对传递对准精度的影响

图3所示的是在不同的延迟时间误差下，水平直线飞行（1 g加速）条件下的对准结果。图4所示的是在相同的延迟时间误差（10ms）下，水平直线飞行加速度分别为1g、2g、3g条件下的对准结果，右图是左图的部分放大。

图3 不同时间延迟误差对对准精度的影响（Sz）

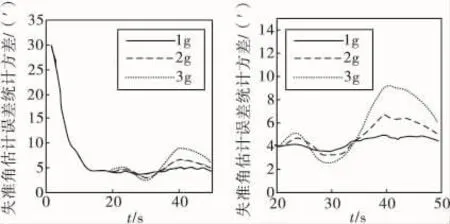
图4 不同机动条件下时间延迟误差对对准精度的影响（Sz）

从图3、图4可以看出，在相同的直线飞行条件下，延迟时间误差小于10ms以下，对失准角估计精度的影响比较小；延迟时间误差为10～20ms，在机动段对失准角估计精度的影响较大，如果延迟时间误差大于20ms，则对失准角估计精度的影响很大。而且直线加速度越大，失准角估计误差也越大。在水平转弯飞行的条件下，也可以得出相同的结果。因此，在工程应用中，一般要求延迟时间误差小于10ms，仿真时可选取其在－5～＋5ms范围内均匀分布。

6 结论

设计弹载捷联惯导传递对准算法时，机载主惯导火控系统信息精度对对准精度影响很大。文中分析了弹载捷联惯导传递对准中火控匹配信息在武器系统中的功能作用以及传递对准对火控信息的精度要求。通过仿真，给出了火控信息的更新周期和信息传输的延迟时间误差对传递对准的影响结果。对算法的工程化实现具有指导作用，其结论可以推广到其它类型的导弹中。

[1]以光衢.惯性导航原理[M].北京：航空工业出版社 ，1987：169－171.

[2]赵利强，蒲一平.空空导弹动基座对准基准及误差分析[J].航空兵器，1998（4）：4－7.

[3]鲁浩，杜毅民，尉新亮.空空导弹惯导系统传递对准中飞机主惯导参数的应用[J].航空兵器，2000（1）：1－3.

[4]鲁浩，杜毅民，王纪南.应用于近距空空导弹惯导系统的传递对准技术[J].中国惯性技术学报，2005，13（5）：10－15.

[5]David H Titterton，John Weston.捷联惯性导航技术[M].张天光，王秀萍，王丽霞，等，译.2版.北京：国防工业出版社，2007：253－254.