多特征互补的红外与光学图像匹配方法＊

周 伟，刘 丰，刘 婧

（第二炮兵工程学院，西安 710025）

0 引言

图像特征作为图像的表征之一被广泛应用于图像处理领域中，尤其在多传感图像匹配识别中，由于二者图像灰度差异大，采用基于灰度的匹配方法产生较大的误差，而提取多传感器图像之间的不变特征进行匹配，成为解决这一问题的有效途径[1]。

尺度不变特征变换[2]（scale invariant feature transform，SIFT）是目前国内外特征点匹配研究领域的热点与难点，其匹配能力较强，可以处理两幅图像之间发生平移、旋转、仿射变换情况下的匹配问题。SIFT算法在特征检测阶段采用DoG算子检测特征，该检测子主要检测团块类目标，但对于多源图像，如可见光与红外图像，其灰度差异较大，DoG检测到的特征重复率低，从而影响匹配率。针对这一问题，对于光学与红外图像，分别检测DoG与Harris－Laplace特征，同时提出了一种改进的DoG检测算法，改善了特征的分布，并将两特征用SIFT算子描述，之后进行匹配，实验结果表明，文中方法有效提高了匹配率。

1 DoG检测子

兴趣点检测是图像匹配算法中关键的一步，特征并不是越多越好，过多特征在生成描述子时需要大量时间，而且还影响匹配精度。因此文中提出了一种改进的DoG检测子，在不影响特征表征性的前提下，改善特征在图像中的分布，从而提高检测精度。

1.1 DoG检测子

为了在尺度空间检测到稳定的关键点，SIFT采用高斯差分尺度空间（DoG scale－space），即利用不同尺度的高斯差分核与图像卷积生成。

DoG算子计算简单，是尺度归一化的LoG算子的近似。图像金字塔的构建：图像金字塔共O组，每组有S层，下一组的图像由上一组图像降采样得到。图1是两组高斯尺度空间图像示例金字塔的构建。

图1 高斯差分与图像金字塔示意图[3]

为了寻找尺度空间的极值点，每一个采样点要和它所有的相邻点比较，看其是否为图像域和尺度域的极值。如图2所示，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。之后进行像素的预筛选，小于一定阈值的像素点被排除。图3中左边图像为DoG检测子的检测结果。

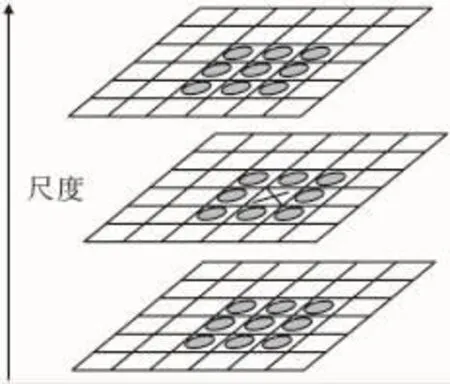
图2 DoG空间局部极值检测

1.2 改进DoG检测子

其中xi是特征点位置，O是所有特征点位置的集合，cr是鲁棒性参数（可以设置为0.9）。这样就保证了非极大值抑制的像素邻域是不同的。

上述思想虽然改善了兴趣点的分布，但花费时间较原DoG算法多，因此，文中不是顺序的遍历整个尺度空间来寻找关键点，而是随机搜索尺度空间，直到找到所需的特征点个数为止。

DoG主要用来检测团块类目标，因此兴趣点也主要位于团块区域，即明显比背景暗或亮的区域，局部极值不可能位于平坦区域或其邻域。局部极值的另一个可能位置为毛刺区域，例如灰度快速改变的狭窄区域。但由于构建DoG尺度空间时，对图像进行了多次平滑，只有粗尺度中信息被保留，而且毛刺被滤除。因

为了使特征点更好的分布于图像内，文中对DoG检测子进行了改进，即在更大的范围中检测极值。即在当前尺度长度为2r的邻域内，以及上下相邻尺度9×2个点共（4r2－1＋18）个点比较，r定义如下：此，文中改进算法包含两个步骤：首先对于一个点xi，DoG（xi）大于一定阈值时，即为团块区域，之后判断该点是否为局部极值，当发现局部极值或给定的试验次数满足时搜索结束；如果DoG（xi）小于一定阈值时为非团块区域，该区域的搜索结果忽略，搜索从其它位置重新开始。算法描述见表1：

表1 改进DoG算法

图3 DoG检测子与改进检测检测结果

图3为两算法检测结果比较，左边图像为DoG算法检测结果，共检测到121个关键点，右边图像为改进算法当Num设置为30时的检测结果，由图中可以看出，改进算法可以减少特征点检测数量，使特征更好的分布于图像内，利于后续的匹配识别。最后的实验结果将说明改进DoG算法优于原算法。

2 Harris－Laplace检测子

DoG检测特征时，为了得到更加稳定的特征点，消除了边缘点。对于多源图像来说，其灰度差异大，而边缘信息是至关重要的。因此，在特征检测阶段，引入Harris－Laplace检测子，它可以检测角点类型的特征，这样可以弥补DoG检测子的不足。Harris－Laplace检测子是 Mikolajczyk and Schmid[4]提出的具有尺度不变性的检测子，其检测步骤为：

Step1：在尺度空间中用Harris[5]检测子寻找极值点。Harris角点检测矩阵为：

局部图像导数由尺度为σD（微分尺度）的高斯核计算得到。矩阵的特征值表示点的邻域两个正交方向上主要信号的改变。实际应用中，用下式来检测角点：

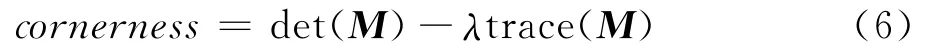
而det（M）表示矩阵M行列式的值，而trace（M）表示矩阵M的迹。采用非极大值抑制可以提取cornerness函数的局部最大值作为角点。Harris角点具有平移和旋转不变性，而且在光照条件变化时也很稳定。

Step2：在上一步所求极值点的空间位置上，寻找极值点所在尺度邻域（如0.7σ～1.4σ）内LoG函数响应的极值点。LoG函数定义为：

Step3：在第二步所求的极值点尺度上，用Harris Detector寻找极值点所在空间邻域内的极值点。

Step4：如果第三步极值点的位置发生了变换，则返回到第二步，如此反复，直到最后求得的极值点在空间上的Harris Detecor和尺度邻域内的LoG空间同时取得极值。

通过上述步骤检测出的区域具有尺度不变性。图4为可见光与红外图像分别检测到的Harris－Laplace特征。

图4 可见光与红外水塔图像Harris－Laplace特征

3 SIFT描述子

对于上述改进的DoG检测子与Harris－Laplace检测子检测到的关键点都具有三个信息：位置、所处尺度、方向。之后将每个关键点采用SIFT描述子进行描述。首先将坐标轴旋转为关键点的方向，以确保旋转不变性。

图5 由关键点邻域梯度信息生成特征向量[6]

接下来以关键点为中心取8×8的窗口。图5左部分的中央黑点为当前关键点的位置，每个小格代表关键点邻域所在尺度空间的一个像素，箭头方向代表该像素的梯度方向，箭头长度代表梯度模值，图中的圆圈代表高斯加权的范围（越靠近关键点的像素梯度方向信息贡献越大）。然后在每4×4的小块上计算8个方向的梯度方向直方图，绘制每个梯度方向的累加值，即可形成一个种子点，如图5右部分所示。此图中一个关键点由2×2共4个种子点组成，每个种子点有8个方向向量信息。这种邻域方向性信息联合的思想增强了算法抗噪声的能力，同时对于含有定位误差的特征匹配也提供了较好的容错性。实际计算过程中，为了增强匹配的稳健性，Lowe建议对每个关键点使用4×4共16个种子点来描述，这样对于一个关键点就可以产生128个数据，即最终形成128维的SIFT特征向量。

4 实验结果与分析

为了验证文中算法的有效性，在Pentium 4，3.0 GHz CPU，2.0GRAM的PC机上采用Matlab编程实验了文中所提算法。对5组场景的可见光与红外图像进行了试验，SIFT算法采用DoG＋SIFT，而文中算法采用改进DoG＋Harris－Laplace＋SIFT，实验结果如表2所示。

表2 算法比较结果

由于篇幅限制，这里只给出第一组场景的匹配图像，如图6所示。由图中可以看出，采用原SIFT算法有2个匹配点对，其中1个为误匹配，正确率为50%，而采用文中算法有53个匹配点对，其中2个为误匹配点，正确率为96.2%。

图6 SIFT算法与改进SIFT算法匹配结果比较

对于本算法中，随着关键点的增多，算法的时间复杂度也增加，实际应用中，为了满足实时性，可以采用许多加速算法，如用积分图像加速高斯滤波过程，用DoM代替DoG，用PCA－SIFT代替SIFT等，这都可以加速算法执行。

由表2可以看出，算法1对于多源图像匹配效果不好，匹配点非常少，而且正确率很低。而文中算法针对传感器图像灰度差异大，SIFT算法中DoG检测子检测团块类目标受灰度影响大，容易造成误匹配的问题，在特征检测阶段，将DoG特征与Harris－Laplace特征相结合，同时为了消除DoG特征对算法正确率的影响，对其进行了改进，在不影响特征表征性的同时，减少DoG特征的数量，从而在提高匹配正确率的同时，有效减少了误匹配点，这对于多源图像匹配识别来说是至关重要的。

[1]Thourn K，Kitjaidure Y.Multi－view shape recognition based on principal component analysis[C]//Advanced Computer Control，ICACC′09，2009：265－269.

[2]Lowe D G.Distinctive image features from scale－lnvariant keypoints[J].International Journal of Computer Vision，2004，60（2）：91－10.

[3]Song R，Szymanski J.Well－distributed SIFT features[J].Electronics Letters，2009，45（6）：308－310.

[4]Mikolajczyk K，Schmid C.Scale and affine invariant interest point detectors[J].International Journal of Computer Vision，2004，60（1）：63－86.

[5]Harris Stephens M.A combined corner and edge detector[C]//Alvey88，1988：147－152.

[6]Lowe D G.Local feature view clustering for 3Dobject recognition[C]// Proc.of the IEEE Conference on Computer Vision and Pattern Recognition，2001.