光纤陀螺随机漂移时间序列建模研究＊

陈俊杰，杨孟兴

（中国航天科技集团第16研究所，西安 710100）

0 引言

FOG与传统机电陀螺相比有许多突出的优点，如耐冲击、抗震性好、测量范围大、对重力加速度不敏感，但使其达到较高精度的成本很高，反而显示不出其工程应用上最重要的优点。FOG输出的误差主要包括：常值漂移及随机漂移。常值漂移可通过标定方法进行消除，而随机漂移作为衡量FOG精度一个非常重要的指标，且其长时间工作过程中会随时间发生变化，对惯导系统产生较大的影响。目前，FOG随机漂移建模还是一个难点，难点在于如何简单而有效地将随机漂移减弱到最低限度，使惯导系统的精度得到最大程度的提高。在工程应用中，一般通过工艺改进等手段从硬件上进行减小随机漂移，但不管如何改进都会有一个局限性，而且每增加一个精度级别会花费大量成本。若能通过一定的软件措施，在FOG精度不够时使其达到应用要求，是非常有意义的。文中通过建立线性自回归模型（AR）及非线性自回归模型（NAR），讨论其建模过程及对随机漂移的补偿效果。

1 AR线性模型与非线性模型

时间序列分析是一种时域分析法，它不仅研究过程的确定性变化，而且更着重于研究过程的随机性变化，它直接利用随机时间序列来建立差分方程，把一个高度相关的平稳随机时间序列表示成一种数字递推的形式（即看成由各时刻相关随机时间序列和各时刻出现的白噪声组成）。

一般地，随机过程Xt（因变元）的观测值与m个自变元u1t、u2t、…umt取值的依赖关系可用线性方程：Xt＝β1u1t＋β2u2t＋…＋βmumt＋εt（1≤t≤N）来描述，并称为m元线性回归模型，其中实数βi（1≤i≤m）称为回归系数，εt是因变元Xt中无法用uit（1≤i≤m）表示的各种随机因素组成的随机干扰，一般称为剩余误差或残差。并假定εt是零均值、方差为σ2ε、相互独立且服从正态分布的随机过程。

在实际问题中，自回归模型所表现的随机过程或时序的观测值｛Xt，t＝0、±1、…｝，与其自身前几个时刻的观测值 Xt－1、Xt－2、… 有关或有依赖性，也称为线性自回归模型，即AR模型：

其中at也需符合εt的要求。

AR非线性自回归模型也称为AR状态依赖时间序列模型，描述如下：给定一个系统，其输入为均值为0、方差为σ2ε的白噪声，该白噪声序列的输出为时间序列｛Xt，t＝0、±1、…｝，则该系统的输入输出关系可以描述为：

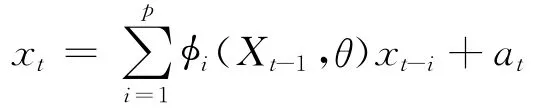
其中：Xt－1＝ （xt－1，xt－2，…，xt－p）为系统的一个状态；φi（Xt－1，θ）xt－i为Rp→R上的光滑函数；参数θ＝ （θ0，θ1，…，θp）∈Θ＝Θ0×Θ1×…×Θp，参数空间Θi（i＝0，1，…，p）是R中的开子集。

2 动态数据预处理

将FOG置于水平测试台上，输入轴水平向东，此时输出均值即为常值漂移。在常温环境下测试其输出，数据如图1所示。

图1 FOG零偏输出序列

根据文献[5]，由平稳性检验算法可得：Z＝0.0464≤1.96；由趋势项检验算法，设置段数为50，可得＝1.9072≤1.96，因此认为FOG静态输出是平稳且无趋势项的。合理性假定认为FOG零偏输出符合正态性要求，因此FOG输出符合平稳、正态的要求，可进行时间序列建模。

通过分析FOG输出的自相关（系数）函数，如图2所示。可知，除了h＝1s外其他相关时间下的自相关系数均落入检验带，这也验证了文献[1]中“FOG中主要存在随机白噪声”的观点。但是FOG输出除了随机白噪声，还是存在着其他噪声，应通过相关模型进行滤除，直到剩下白噪声为止。

3 FOG随机漂移的AR与NAR建模

零均值、平稳以及正态序列的AR（p）模型可表示为：

图2 FOG输出序列的自相关函数

设FOG的静态输出序列为yk（k＝1，2，……），该序列可以看作平稳、正态时间序列，则平稳、正态、零均值时间序列可以表示成：xk＝yk－，（k＝1，2，……），代入上式，可得：

其中常数c＝（1－φ1－φ2－…－φp）[6]。

AR模型可使用Yule－Walker算法进行辨识参数，NAR模型可通过使用最小二乘法辨识参数。由于模型阶数越高，计算量越大，如NAR（2）及NAR（3）在滤波的每一步递推过程中比NAR（1）要多5个和11个乘法运算，对于性能不高的处理芯片，可能会影响解算的实时性，因此在建模中不参考AIC等定阶准则，只对AR（1）～AR（3）和NAR（1）～ NAR（3）进行比较。

使用FOG输出的前1000s数据进行参数辨识，之后使用建立好的模型进行滤波，比较滤波前后的零偏均值及稳定性，如表1所示。

可知AR（1）～AR（3）和NAR（1）～ NAR（3）滤波后零偏值较滤波前相比，差值最大不超过0.0042°／h，这对于滤波前的零偏稳定性0.0166°／h相比，可认为未发生改变；而比较零偏稳定性的改善情况，AR（1）模型的滤波效果比 AR（2）、AR（3）良好，而NAR（1）模型的滤波效果比NAR（2）、NAR（3）良好。

选取AR（1）和NAR（1）模型进行比较：

1）两种模型滤波后均值未造成较大误差，零偏稳定性的改善几乎一样；

2）在滤波递推过程中，AR（1）模型需1次乘法，NAR（1）需3次乘法，乘法带来的延时都是很小的，可以忽略不计。

建立好的模型如下：

表1 AR模型和NAR模型的滤波结果（（°）／h）

图3 经AR（1）和NAR（1）滤波后的零偏输出序列

4 模型适用性检验

检验模型拟合残差是否近似为白噪声是一种常用的适用性检验方法，主要方法有：散点图法、相关系数法和F检验法。相关系数法是普遍采用的一种方法，倘若滤波后输出的相关系数以95.5%的概率在噪声带，则认为残差不存在自相关性，即输出的噪声几乎全为随机白噪声，模型通过适用性检验。

由图4可知，两个模型滤波后输出的自相关（系数）函数都在噪声检验带内，滤波后序列的噪声为白噪声，两个模型均能通过适用性检验。

5 结束语

文中分别使用AR模型与NAR模型对FOG随机漂移进行建模及滤波，通过比较滤波前后均值的偏移情况及随机漂移的改善程度，并考虑递推过程的运算复杂性，综合考虑各因素后，AR（1）和NAR（1）是比较适合用于FOG随机漂移数学模型。在不同精度FOG随机漂移的建模及验证中，也得到相应的结论。在两个模型的作用下FOG的随机漂移都可以得到一个数量级的改善，这对于精度不够的FOG惯导系统而言是可观的。该模型的最大特点是没有采用卡尔曼滤波，更减小了运算量，简单有效，更容易在单片机等计算芯片上实现。下一步的工作是如何将该思路在实际系统上进行应用，实现在线建模及实时滤波。

图4 滤波后输出序列的自相关（系数）函数

[1]张桂才.光纤陀螺原理与技术[M].北京：国防工业出版社，2008.

[2]崔少君，沈晓蓉，柳贵福.动力调谐陀螺静态漂移的非线性时间序列建模[J].中国惯性技术学报，2010，18（3）：343—346.

[3]汤霞清，宗艳桃，郭理彬，等.光纤陀螺随机漂移的ARMA模型[J].装甲兵工程学院学报，2008，22（3）：50—53.

[4]朱奎宝，张春熹，宋凝芳.光纤陀螺随机漂移模型[J].北京航空航天大学学报，2006，32（11）：1354—1357.

[5]吴怀宇.时间序列分析与综合[M].武汉：武汉大学出版社，2004：91－92.

[6]王立冬，张春熹.高精度光纤陀螺信号的在线建模与估计[J].光电工程，2007，34（1）：55－58.