爆炸荷载作用下地下结构破坏模式研究＊

孙惠香，许金余，2，李 庆

（1空军工程大学工程学院，西安 710038；2西北工业大学力学与土木建筑学院，西安 710072）

0 引言

地下工程所处的环境条件和地面截然不同，设计理论并不成熟，尤其是动载荷，长期以来一直采用的是经验的放大系数法，因此，人们一直致力于寻求解决地下工程尤其是动力问题的理论与设计方法。

对于爆炸荷载作用下所有结构的设计和分析问题，必须要考虑结构的牢固性[1]，以确定结构在各种爆炸荷载作用下是否可靠。结构上的荷载与结构运动是相互依赖的，因此，在确定结构的荷载和运动时，必须考虑结构与周围介质之间的相互作用规律，其会影响结构的破坏模式，国内外学者对此作了大量的研究，取得了有意义的研究成果。美国在20世纪70年代就开始进行大量的钢筋混凝土结构抗爆现场模型试验，得到了浅埋结构的破坏模式，Ghabossi J、Krauthammer T[2－3]等对混凝土梁的破坏进行了详细研究，国内解放军理工大学的方秦教授[4]、清华大学的陈肇元教授[5]也对冲击和爆炸荷载作用下钢筋混凝土构件和浅埋结构动力响应进行了系统研究，华南大学的魏德敏教授对于冲击荷载作用下的拱形结构的动力响应和动力屈曲进行了系统研究[6]，但是对于最常见的深埋于地下的拱形结构破坏模式的研究还比较少。

由于试验研究的难度很大，地下结构的动力响应和破坏特征的研究，早期采用的一般是简化模型求解方法，随着计算机的发展，有限差分法和有限单元法等数值方法成为处理结构与介质相互作用问题的最有效方法，因此文中拟采用有限单元法模拟处于岩石当中的地下拱形结构在爆炸荷载作用下与围岩之间的动力相互作用机理，并对不同起爆位置、不同跨度的结构破坏模式进行研究，以指导地下防护工程设计。

1 数值模拟

文中应用 ANSYS／LS－DYNA程序在不同的TNT当量炸药、不同的装药位置下，对各种跨度的地下结构进行数值模拟。

1.1 数值模拟方案

结构跨度l为6m、14m、24m、40m的直墙拱结构，直墙高为2m，拱高f分别为5m、6m、6.5m和12m，支护结构为50cm的混凝土结构。由于岩石等固体爆炸要比空气和水中爆炸复杂的多，与岩石的物理力学特性息息相关，岩石的结构构成、坚硬程度、密度、容重、脆涨性、波阻抗等等均会影响应力波的传播，现做以下假定：岩石类型为花岗岩，将岩体宏观上看成连续、各向同性的均质体，不计实际上存在的节理裂隙影响；为封闭式爆炸。由于洞室为细长结构，厚度取5m进行三维模拟，横向模拟范围为结构两边各取5m范围岩体。由于岩体是无限远的，边界在无限远处，为了和实际相符，将无反射边界条件实现于计算模型中。

由于结构对称，为节省计算机时，建立1／4模型，炸药尺寸为：100cm×50cm×50cm，50cm×50cm×50cm，装药量为407.5kg，203.75kg。炸药采用中心起爆。

1.2 单元选择和材料模型

1）炸药单元的材料模型参数设置

炸药单元选用＊MAT＿HIGH ＿EXPLOSIVE＿BURN模型，用JWL状态方程描述爆炸过程压力和内能及相对体积的关系。岩石为花岗岩，按弹塑性材料考虑，选用塑性动力学模型 MAT＿PLASTIC＿KINEMATIC模型。支护结构为钢筋混凝土结构，采用JOHNSON－HOLMQUIST－CONCRETE材料模型，该模型综合考虑了大应变、高应变率、高压效应，考虑了损伤及损伤积累，具体参数见文献[8]。

2）算法选择

LS－DYNA程序具有Lagrange、Euler和ALE算法，文中采用流固耦合算法来描述爆炸过程，炸药看作是流体，围岩和结构是固体，对炸药采用ALE算法，对结构和围岩采用Lagrange算法，通过流固耦合方式（＊CONSTRAINED＿LAGRANGE＿IN＿SOLID）来处理各种物质间相互作用[7]。

1.3 数值模拟结果验证

目前常用来求算破碎区半径的公式为[8]：式中：Pd为冲击波作用在孔壁岩石上的初始冲击压力；R0为装药半径；ST为岩石抗拉强度；λ为系数，λ＝υ／（1－υ），υ为岩石的泊松比；α为应力波衰减指数，α＝2－υ／（1－υ）。

由图1可见，模拟中孔壁岩石的初始冲击压力为138MPa，ν ＝0.27，则 λ ＝0.37，α＝1.73。将装药按体积相等转换成球形装药，其半径为199.52cm，根据经验公式（1）计算的岩石裂隙区半径为：RT＝556.67cm。模拟中图2为岩石破碎区，岩石的破碎区外半径根据单元尺寸经计算为570cm，与经验公式计算数值甚是相近，经验证表明：模拟模型建立、材料模型选用和算法选择合理。

图1 孔壁岩石的初始压力

图2 爆炸坑破碎区

2 数值模拟结果分析

2.1 结构与围岩相互作用研究

装药爆炸以后，爆腔中充满高温高压气体，由于气体的向外膨胀，产生了球面纵波开始向外传播，形成了冲击波阵面，随着距爆心距离的增大，开始形成一个震荡脉冲，并开始在岩石中传播，当波传播到支护结构与围岩的接触面时，由于混凝土和岩石是两种不同的材料，在界面一部分发生反射，一部分穿透混凝土，成为透射波，反射波反向传播，与正向传播的加载波相遇，将会出现卸载现象，波幅减小。波在自由表面反射后，支护结构表面混凝土开始被震塌，随着震塌继续发展，最后围岩与结构将随着跨度的不同发生不同模式的破坏[9]。

从图3中可以看出，在拱的跨度较小（6m）时，第一个峰值压力来临时，整个拱各质点的压力相差不大，拱顶和靠近拱脚即直墙顶部质点D的峰值压力最大，但此时压力只有大约7MPa，并不会造成支护结构破坏，质点A接下来几个峰值反而减小，主要是由于反射波的卸载造成，最后当最大峰值来临时，并没有出现在拱顶，仍然是拱肩处的D质点，高达278MPa，岩石的动态抗压强度为117MPa，此时岩石早已屈服，混凝土也已经屈服，说明拱是由于拱肩处混凝土的破坏而发生的破坏。随着装药和离拱顶起爆距离的增大，并没有从本质上改变拱的受力状态，图4是装药为407.5kg，距拱顶10m时的支护结构界面接触力，仍然是拱肩处混凝土峰值压力最大。

图5和图6分别是24m跨和40m跨拱的压力时程曲线，由图可以看出，随着拱的跨度的增大，拱和围岩的相互作用力越来越小，拱的峰值压力也随跨度成反比例减小，反复拉压的区域缩小，拱的最大压力出现在拱顶附近，对于40m跨拱，随着拱的跨度的增大，拱肩处压力不断减小，但均没有达到混凝土的抗压屈服强度，所以拱是由于下部受拉产生的弯曲破坏。

从图7～图12中可以看出，拱发生X和Y两个方向的位移，整个拱的竖向变形都经历第一个峰值，第一个峰值后，随着截面位置的不同，质点位移的变化趋势发生了不同的变化，拱顶处质点的竖向位移不断增大，说明该处结构发生破坏，而距拱顶一段距离的质点的竖向位移则趋于稳定，说明拱发生的是局部破坏，跨度较小时，横向应变率较大，经历一个峰值会趋于稳定，而跨度较大时（24m），应变率较稳定，横向变形逐渐增大，说明弯曲变形占主要地位。

图3 6m拱界面接触力（A、B、C、D分别为由拱顶到拱肩的质点，以下图同）

图4 6m拱界面接触力

图5 24m拱界面接触力

图6 40m拱界面接触力

图7 6m拱Y方向位移

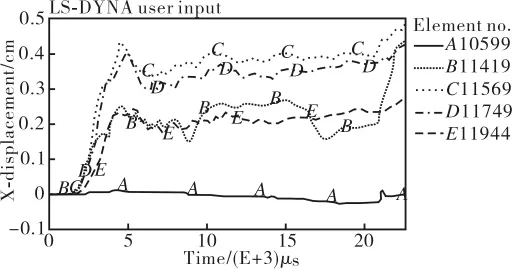
图8 6m拱X方向位移

图9 24m拱Y方向位移

图10 24m拱X方向位移

2.2 结构与围岩破坏模式分析

地下结构多为拱形结构，拱形结构在横向冲击时，将发生弯曲运动和剪切运动，当拱经受不同的波传播时，随着跨度和装药位置不同，会得到不同的破坏模式，经过一系列的模拟，根据前面分析，拱的破坏模式与波的性质、爆心距和跨度有很大的关系。主要有以下几种破坏模式：

图11 40m拱X方向位移

图12 40m拱Y方向位移

1）整体破坏

经过大量的数值模拟发现，不论跨度有多大，只要装药位置距离拱顶距离很近时，则均发生整体破坏，支护结构全部破坏，围岩坍塌。如图13所示，当203.75kg的TNT炸药在拱顶1m处爆炸时，拱发生了整体破坏。

2）局部破坏

当起爆点离拱顶有一定距离时，随着距离的不同、炸药量的多少和跨度的不同会发生以下几种破坏形式：

①剪切破坏

拱在弯曲波作用下，实际上一方面是弯矩扰动，一方面是剪力扰动，为二者耦合的结果，当拱中剪力扰动引起的剪应变最先达到使拱失效的时候，剪力在拱的破坏中将起主要作用，设梁的横向变形为u，则剪切应变当剪切应变超过动态屈服应变时，拱上出现剪切铰，剪切塑性铰先于弯曲塑性铰出现时，结构的破坏是由于剪切铰沿拱的横方向传播使整个截面均屈服，即出现剪切塑性铰，拱将发生剪切破坏。模拟中，由前面分析，在拱的跨度较小时（6m），爆心距离距拱顶不太远（3m）时，一般会在拱肩处发生剪切破坏（见图14）。

图13 1m爆距拱的整体破坏（6m跨）

②弯曲破坏

当弯曲波在拱中传播，弯矩扰动占主要作用时，则弯曲铰会在剪切铰之前出现，随着弯曲铰在拱横向的传播，截面屈服出现弯曲塑性铰，从而发生弯曲破坏，模拟中发现，当装药位置离拱顶较远时，比如6m跨拱当装药距离拱顶15m，或当拱跨度较大时（24m），拱发生弯曲破坏，见图15和图16。

图14 3m爆距拱的剪切破坏（6m跨）

3）受拉破坏

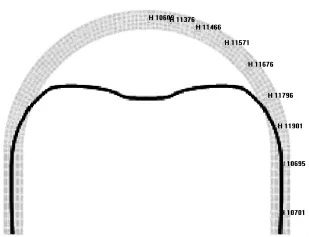
图15 15m爆距拱的弯曲破坏（6m跨）

当拱的跨度更大时（40m），拱由于自由面的扩大，承受更大的拉力，由图17和18可以看出，质点的主拉应力要远远大于主压应力，拱将由于主拉应力的破坏而发生受拉破坏。

图16 5m爆距拱的破坏（24m跨）

图17 40m拱的主压应力

图18 40m拱的主拉应力

3 结论

通过对各种跨度地下拱形结构在不同起爆位置和不同装药的数值分析，可以得出：

1）经过模拟，岩石的破碎区半径经计算与经验公式基本一致，表明数值模拟方案合理。

2）爆炸荷载作用下，接触面和自由面应力波多次透射与折射致使结构与围岩经受反复拉压，跨度较小（6m）时，装药位置距拱顶距离不太大时，拱肩处均为受力的薄弱环节，结构是以剪切破坏为主要模式，随着装药位置距拱顶位置增大（15m）和拱跨度的增大（24m），结构与围岩之间相互作用力减小，拱将以弯曲破坏为主要破坏模式。

3）对于大跨度（40m）结构，爆炸荷载作用下，由于自由面的扩大，主拉应力远远大于主压应力，由于岩石抗拉强度低的特点，拱将发生受拉破坏。

[1]美国空军防护结构设计与分析手册[Z].1974：209－210.

[2]Ghabossi J，Millavec W A，Isenberg J.R／C structures under impulsive loading[J].Journal of Structural Engi－neering，1984，110（3）：505－522.

[3]Krauthammer T.Shallow－buried RC box－type structures[J].Journal of Structural Engineering，1984，110（3）：637－651.

[4]陈肇元.防护工程钢筋混凝土构件的抗剪性能与设计方法[J].防护工程，1994，16（1）：1－7.

[5]方秦.爆炸荷载作用下钢筋混凝土结构的动态响应与破坏模式的数值分析[J].工程力学，2007，24（2）：135－144.

[6]魏德敏.拱的非线性理论及其应用[M].北京：科学出版社，2004：99－160.

[7]白金泽.LS－DYNA3D理论基础与实例分析[M].北京：科学出版社，2005：75－103.

[8]宗琦.岩石内爆炸应力波破裂区半径的计算[J].爆破，1994，11（2）：15－17.

[9]李翼棋，马素贞.爆炸力学[M].北京：科学出版社，1992：370－372.

[10]王礼力.应力波基础[M].北京：国防工业出版社，1983：300－305.