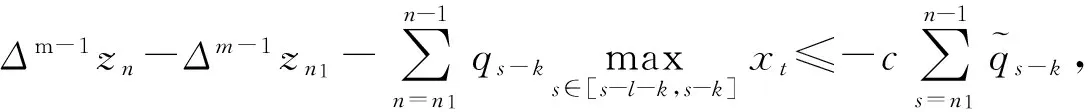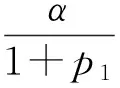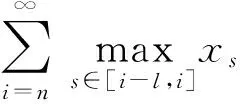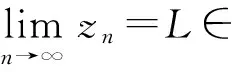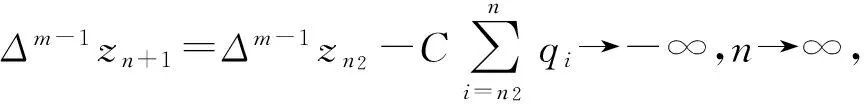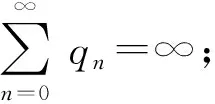带有极大值项的奇阶中立型差分方程的渐近性
高艳花, 钟晓珠,刘 娜, 李国琴,赵所所
(燕山大学 理学院 河北 秦皇岛 066004)
带有极大值项的奇阶中立型差分方程的渐近性
高艳花, 钟晓珠,刘 娜, 李国琴,赵所所
(燕山大学 理学院 河北 秦皇岛 066004)
考虑了一类带有极大值项的奇数阶中立型差分方程的非振动解的渐近性,得到了该类方程的解非振动的一些充分条件,推广了已有文献的相关结果.
奇数阶中立型差分方程; 非振动解; 极大值; 渐近性
0 引言
考虑中立型差分方程
(1)
其中,{pn}是实数列,{qn}是非实数列.n∈N(n0)={n0,n0+1,…},l和k为正整数,且k≥l,m为正奇数,Δ=xn+1-xn.
当m=1时,方程(1)变为
(2)
对于方程(2)的振动性及渐近性,文[1-2]得到了一些好的结果.当m=2时, 方程(1)为二阶中立型差分方程,文[3-6]讨论了此类方程的振动性和渐近性.当m>2时,文[7]仅讨论了方程解的振动性问题,也得到了一些充分条件.本文将讨论m大于1的奇整数的情形下方程(1)的非振动解的渐近性问题.
方程(1)的解{xn}称为非振动的,如果{xn}最终为正或最终为负;否则称{xn}为振动的,即{xn}既不最终为正也不最终为负.
本文中,定义{zn}为
zn=xn+pnxn-k,
(3)
则方程(1)可变形为
(4)
1 基本引理
引理1[5]若当n≥n0时,zn>0且Δmzn(≠0)是常号的,则存在整数i(0≤i≤m)满足:当Δmzn≤0时,i+m为奇数;当Δmzn≥0时,i+m为偶数.并且,对充分大的n,
(i)当i≤m-1时,(-1)i+jΔjzn>0,i≤j≤m-1;
(ii)当i≥1时,Δjzn>0,1≤j≤i-1.
引理2[6]若存在常数p<0使得p 定理1假设下列条件满足: H1pn≡1; 证明设{xn}是方程(1)的最终正解,则zn=xn+xn-k>0.由(4)知Δmzn≤0成立,所以{Δm-1zn}为非增数列.因为qn不恒等于0,所以Δmzn也不恒等于0. (5) (6) (7) 既然{Δm-1zn}为正的非增数列,则{Δm-1zn}必有正的下界.另一方面,H2意味着当n→∞时(7)的右端式子趋于负无穷.因此有 (8) 对(4)从n1到n-1求和得 (9) 定理2假设下列条件满足: H3-1≤p1≤pn≤0; 证明设{xn}是方程(1)的最终正解,且(3)成立.由引理2可知zn满足引理2中的(i)或(ii). xn+k=zn+k-pnxn≤α-p1xn≤α-p1M,N2≤n≤N2+k. 从而D=0. 定理3假设下列条件满足: H5假设存在q,使0≤q≤qn; H6{pn}是有界非负实数列. 证明设{xn}是方程(1)的最终正解,且(3)成立.则由H6知zn>0.由H5知Δmzn≤0,所以{Δm-1zn}为非增序列.对于Δm-1zn有以下两种情形: (a)Δm-1zn→-∞,n→∞. (b)Δm-1zn≥0.且Δm-1zn→L,其中L是有限实数.(L>0,L<0,L=0). 若(a)成立,则存在n2≥n0使Δm-1zn2≤0.当n>n2时 Δm-1zn<Δm-1zn2≤0, (10) 定理4假设下列条件满足: H7存在常数p∈[0,1],使0 再设{xn}是方程(1)的一个最终负解,同样可知结果成立. 定理5假设下列条件满足: H10pn≡0, (a*)Δm-2xn→+∞,n→∞; (b*)Δm-2xn→L*,n→∞.其中L*是有限实数. 类似引理2的讨论,我们可得到:情形(a*)不真而情形(b*)为真且L*=0.类似上面的过程,可得 [1] 罗交晚,刘正荣,俞元洪.带有极大值项的中立型差分方程的振动性和非振动性[J].应用数学学报,2002,25(3):385-391. [2] 范彩霞,赵爱民.带有极大值项的中立型差分方程解的振动性[J].山西大学学报:自然科学版,2005,28(1):5-7. [3] 刘召爽,李巧銮.含最大值项二阶中立型差分方程的渐近性[J].数学研究与评论,2006,2(26):191-198. [4] Luo J W, Bainov D D.Oscillatory and asymptotic behavior of second-order neutral difference equations with maxima [J].Computational and Applied Mathematics,2001,131(1/2):333-341. [5] 张广,高英.差分方程的振动理论[M].北京:高等教育出版社,2001. [6] 刘一龙,杨甲山.一类二阶超线性中立型时滞差分方程的有界振动性[J].郑州大学学报:理学版,2008,40(2):24-28. [7] 周效良,高学亮.带有最大值项的高阶中立型差分方程的振动性[J].数学的实践与认识,2008,38(11):173-177. SomeAsymptoticalPropertiesofOddOrderNeutralDifferenceEquationswithMaxima GAO Yan-hua,ZHONG Xiao-zhu,LIU Na,LI Guo-qin,ZHAO Suo-suo (SchoolofScience,YanshanUniversity,Qinhuangdao066004,China) The asymptotical properties of all non-oscillatory solutions of a class of odd order neutral difference equations with maxima were studied.Some sufficient conditions for all solutions to be non-oscillatory were obtained.Thus, the existing literature conclusions were improved and extended. odd order neutral difference equation; non-oscillatory solution; maxima; asymptotical properties O 175.7 A 1671-6841(2011)03-0027-04 2010-06-17 河北省教育厅科学研究项目,编号Z2007431. 高艳花(1982-),女,硕士研究生,主要从事差分方程理论研究,E-mail:gaoyanhuagao@163.com.

2 主要结论及证明