基于最优激励轨迹的RRR机械臂动力学参数辨识
娄玉冰,王东署
(郑州大学 电气工程学院 河南 郑州 450001)
基于最优激励轨迹的RRR机械臂动力学参数辨识
娄玉冰,王东署
(郑州大学 电气工程学院 河南 郑州 450001)
机器人动力学参数的精确辨识是对机器人进行精确控制的前提,参数辨识的精度与所采用的标定轨迹直接相关.以RRR机械臂为研究对象,建立该机械臂的动力学模型.在动力学参数辨识时,选择有穷傅里叶级数做为最优激励轨迹的表达式,通过最小化退化矩阵的条件数来获得最优激励轨迹中的参数,同时把各关节位置、速度和加速度的物理约束与激励轨迹结合起来,使获得的最优激励轨迹在物理意义上是可行的.通过在激励轨迹中指定频率范围来避免激励机器人的柔性特性,利用最小二乘法来辨识动力学参数.最后仿真验证了该辨识方法的有效性.
最优激励轨迹; 参数辨识; RRR机械臂; 条件数
0 引言
由于机器人动力学参数辨识的精度与目标轨迹直接相关,所以标定时必须首先确定标定轨迹.文[1]首先提出了最优激励轨迹(optimal exciting trajectory)的概念,即存在外界扰动的情况下,能对动力学参数进行可靠、充分、快速和精确辨识的轨迹,并通过最小化“信息矩阵”的条件数来获得最优激励轨迹.该方法的缺点在于:优化过程中轨迹约束难以确定且计算量较大,获得的激励轨迹是点阵而非连续曲线;不能通过指定激励轨迹的频率来避免激励机器人的柔性特性;没有对要搜索的轨迹空间进行约束,可能产生不充分的优化过程,即获得的解可能是局部最优解.此后,在动力学参数辨识中,许多学者开始研究最优激励轨迹[2-5],但都是在文[1]的基础上进行了一些改进.
文[6-9]基于多维腕力传感器、基座力传感器的输出信号等方法对机器人连杆动力学参数进行了辨识.文[10]用一种改进的遗传算法对体操机器人的动力学参数进行辨识, 这种方法只需将机器人自由运动和仿真的响应曲线进行比较,就能精确辨识其动力学参数.文[11]用D-H方法对机器人进行运动学分析,为建立机器人动力学模型奠定了基础.文[12]运用实验识别方法得到机器人模型,并用最大似然估计法得到参数的估计值.文[13]提出一种基于六维力/力矩传感器的模块化机器人惯性参数辨识的方法.文献[6-13]对机器人动力学参数辨识进行了卓有成效的探索,但都没有将动力学参数辨识与最优激励轨迹结合起来,参数辨识结果不够精确.
本文以三自由度RRR机械臂的动力学参数辨识为例,采用有穷傅里叶级数作为机械臂各关节最优激励轨迹的表达式,通过最小化退化矩阵的条件数获得各激励轨迹中的参数,并把激励轨迹与各关节的位置、速度和加速度结合起来,确保所获得的最优激励轨迹在物理意义上可行,通过最小二乘法来辨识各关节的动力学参数.
1 RRR机械臂的动力学模型
图1为一个典型的三自由度RRR机械臂的运动学模型,表1中数据为该机械臂的D-H参数值:扭转角αi,连杆长度ai,角位移qi,连杆偏移量di.

图1 RRR机械臂的运动学模型Fig.1 Kinematic modle of an RRR robotic arm

表1 RRR机械臂的DH参数

(1)
其中q为关节运动矢量,
q=[q1q2q3]T.
(2)
(3)
机器人动力学模型可由拉格朗日-欧拉方法得到,模型的标准形式为

(4)
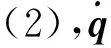
(5)

ijr=[xjyjzj1]T.
(6)
动力学模型(4)可以用基本参数集(base parameter set, BPS)的元素[14]来线性表示,这些元素可由惯性参数非线性组合得到,动力学模型可以转化为线性形式,

(7)
R∈R3×15是退化矩阵,p∈R15×1是基本参数集组成的矢量.

Φ·p=τ,
(8)
其中,
(9)
2 最优激励轨迹的设计
确定各关节最优激励轨迹时,考虑到标定过程中存在测量噪声、外界扰动和随机误差,希望每个关节的激励轨迹最好满足下列指标:采用周期函数,可以连续重复辨识试验,通过对测量的时域数据进行平均化处理提高试验数据的信噪比;可以通过设置频率范围来避免机器人的柔性效应;计算量小,能实现快速的参数辨识.有穷的傅里叶级数可以很好地满足以上条件,所以采用式(10)来表示各关节的最优激励轨迹.

(10)
3 激励轨迹参数的优化指标
由于矩阵条件数的大小是衡量矩阵“好”或“坏”的标志,条件数大到一定程度时,方程组的性态就会发生变化,变成病态方程,小的误差就可能会引起解的失真;条件数最小(接近1)时,方程组的状态最好[16].因此各关节激励轨迹中的参数ai,j和bi,j可通过最小化退化矩阵(9)的条件数获得.
优化后所获得的各关节的最优激励轨迹如图2所示,此时Φ的条件数最小达到1.572 0.与该最优激励轨迹对应的τi如图3所示(i=1,2,3).

图2 最优激励轨迹Fig.2 The exciting trajectories for each joint

图3 最优激励轨迹对应的各关节的输入力矩Fig.3 The torques for each joint
4 参数的线性最小二乘辨识及验证
由于待辨识参数是非时变的,可以用最小二乘法进行估计.在式(8)中通过退化矩阵Φ的广义逆矩阵Φ*即可得到待辨识的参数矢量,
Pls=Φ*τ=(ΦTΦ)-1ΦTτ.
(11)
从关于激励轨迹参数的优化指标的论述中可以看到,Φ的条件数的大小直接衡量了Φ与τ的扰动对最小二乘辨识结果Pls的影响的大小.辨识结果如表2所示.
为验证动力学参数辨识结果的精度,在机器人工作空间内选取一组检验轨迹如图4所示,其中,q1(t)=2sint+cos 10t,q2(t)=3cost,q3(t)=sin 2t.在对应轨迹上运动时,各关节对应的实际力矩与理论力矩对比如图5所示.从图5中可以看到,关节1力矩误差不超过1.5%,关节2不超过2.1%,关节3不超过2.3%,表明动力学参数辨识结果的精度较高.

表2 参数辨识结果

图4 验证轨迹Fig.4 The test trajectories for each joint

图5 各关节实际力矩与理论力矩的对比Fig.5 Compares of the torques for each joint
5 结论
本文以RRR机械臂为研究对象,建立了其动力学模型.参数辨识时,以有穷傅里叶级数作为各关节最优激励轨迹的表达式,通过最小化退化矩阵的条件数作为确定各关节最优激励轨迹参数的性能指标,并把各关节位置、速度及加速度的物理约束与激励轨迹结合起来,使获得的激励轨迹在物理意义上是可行的.通过指定激励频率来避免机器人高频时出现的柔性效应.最后通过仿真验证了该辨识方法的有效性.
[1] Armstrong B.On finding exciting trajectories for identification experiments involving systems with non-linear dynamics [J].The International Journal of Robotics Research, 1989, 6(8):28-48.
[2] Gautier M, Khalil W.Exciting trajectories for the identification of base initial parameters of robots [J].The International Journal or Robotic Research, 1992, 11(4):362-375.
[3] Swevers J, Ganseman C, Tukel D B, et al.Optimal robot excitation and identification [J].IEEE Transactions on Robotics and Automation,1997, 13(5):730-740.
[4] Galafiore G, Indri M, Bona B.Robot dynamic calibration:Optimal excitation trajectories and experimental parameter estimation [J].Journal of Robotic Systems, 2001,18(2):55-68.
[5] Dragan K, Bram D J.Modeling and identification for high-performance robot control:An RRR-robotic arm case study [J].IEEE Transactions on Control Systems Technology, 2004, 12(6):904-918.
[6] 陈恩伟.机器人动态特性及动力学参数辨识研究[D].合肥:合肥工业大学,2005.
[7] 刘正士,陈恩伟,干方建.机器人惯性参数辨识的若干方法及进展[J].合肥工业大学学报:自然科学版,2005,28(9):998-1007.
[8] 于兴永,孙蕾,陈卫东,等.基于基座力传感器机器人连杆惯性参数识别[J].机械传动,2006,30(6):17-22.
[9] 于兴永,干方建,孙蕾.利用牛顿-欧拉动力学识别机器人连杆惯性参数[J].工具技术,2006,40(8):15-18.
[10] 李祖枢,张华,古建功,等.3关节单杠体操机器人的的动动力学参数辨识[J].控制理论与应用,2008,25(2):242-246.
[11] 张常喜,刘广瑞.RV-M1机器人运动学分析[J].郑州大学学报:理学版,2005,37(2):73-76.
[12] 侯扬毅,房海蓉.区间分析理论在机器人动力学参数识别中的应用[J].机械,2008,35(4):64-66.
[13] 黄用华,余跃庆,苏丽颖,等.模块化机器人的惯性参数辨识研究[J].微计算机信息,2007,23(1/2):266-268.
[14] Mayeda H, Yoshida K, Osuka K.Base parameters of manipulator dynamic models[J].IEEE Trans Robot Autom, 1990, 6(2):312-321.
[15] Hensen R H A, Angelis G Z,Molengraft M J G,et al.Grey-box modeling of friction:An experimental case study[J].Eur J Control, 2000,6(3):258-267.
[16] 吴勃英.数值分析原理[M].北京:科学出版社,2003:68-73.
DynamicParameterIdentificationofRRR-RoboticArmBasedonOptimalExcitingTrajectory
LOU Yu-bing, WANG Dong-shu
(SchoolofElectricalEngineering,ZhengzhouUniversity,Zhengzhou450001,China)
Dynamic parameter identification of robot was a precondition for the accurate control of robot,and its precision was directly related to the trajectory chosen.The model of RRR robot dynamics was established.A finite Fourier series was chosen to be the exciting trajectory for each joint.Minimizing condition number of the regression matrix was chosen to be performance index of the exciting trajectory.The exciting trajectory was combined with the limits for positions, speeds and accelerations of each joint.The frequency can be restricted within a permissible bandwidth to avoid the flexibilities.The dynamic parameters were identified on the trajectories with LSM.Finally, the validity of the identification method was proved by the simulation results.
optimal exciting trajectory; parameters identification; RRR-robotic arm; condition number
TP 241
A
1671-6841(2011)03-0108-05
2010-04-21
河南省教育厅自然科学基金资助项目,编号2008A510015,2010B510019.
娄玉冰(1983-),女,硕士研究生,主要从事机器人控制技术研究,E-mail:louyub@163.com;通讯作者:王东署(1973-),男,讲师,博士,主要从事机器人标定与智能控制研究,E-mail:wangdongshu@zzu.edu.cn.

