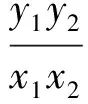这个高考题怎么能不轻松拿下

● (奔牛高级中学 江苏常州 213131)

这个高考题怎么能不轻松拿下

●蒋亦万姝玮(奔牛高级中学 江苏常州 213131)

2011年江苏省数学高考试卷的最大特点之一是难易分明.在解答题部分，大部分学生从第18题的第(3)小题开始就做得很辛苦.从学生的反馈情况来看，数学水平差一点的学生不会做，大部分学生做得模模糊糊，少数比较优秀的学生做得很彻底、心中很踏实.当笔者尝试独立求解之后，很是震惊，此题多么常规、典型，是专题讲解的圆锥曲线问题呐！怎么可以不快速、简捷地拿下呢？

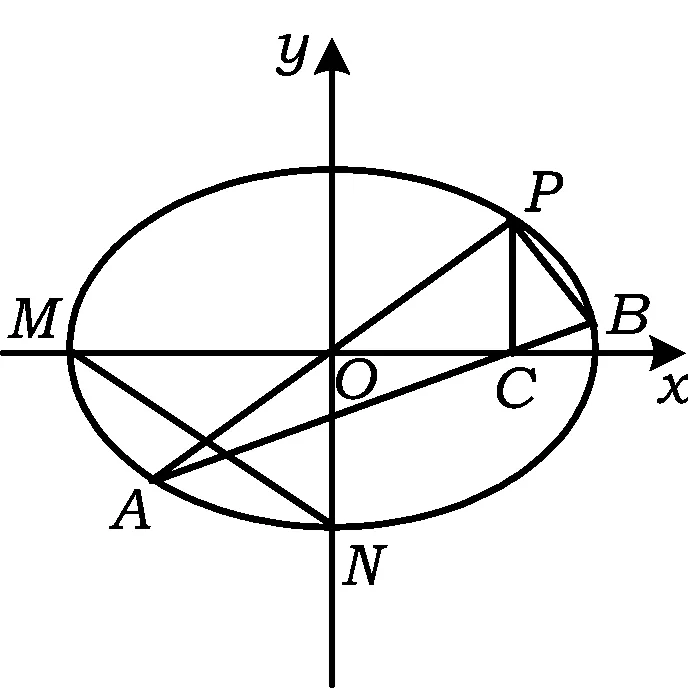
图1

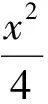
(1)(2)略；

(3)对任意k>0，求证：PA⊥PB．

(2011年江苏省数学高考试题)

方法1由题意，设直线PA的方程为y=kx，与椭圆方程联立方程组

得点A,P的坐标.由点P的坐标求得点C的坐标，从而得到直线AC的方程，再与椭圆方程联立求得点B的坐标.

注方法1虽然思路简单，但可以预见运算复杂，应慎重实施，考虑有没有更简洁的方法.

方法2大胆设点，引入多个变量，最后处理一个多元问题.尝试求解如下：

由题意设P(x0,y0),B(x1,y1),x0>0，y0>0，则点A的坐标为(-x0,-y0),点C的坐标为(x0,0).由点A,C,B共线知，

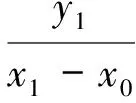
点P,B在椭圆上，从而

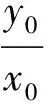
式(2)-式(3)得

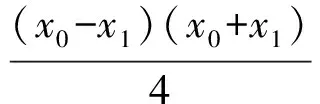
即

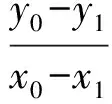
结合式(1)得

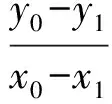
从而

将以上分析过程稍加整理就是第(3)小题的证明.

学生为何不用方法2求证？笔者分析有以下原因:

一是学生缺乏“主动设点、引入多元”解决问题的意识.只会机械地解方程组、求点坐标，即选择了方法1，在计算上花了很长时间，无奈之下稀里糊涂地得到了一个证明，不少环节是蒙的.

二是学生怕多元问题，不敢或者不愿主动设点、引入多个变量.方法2需要学生有较强的观察能力，能灵活处理多个方程式,如得到式(1)、式(2)、式(3)之后怎么处理，这些都是学生解题时的弱项.

在数学高考模拟考试中，多次出现类似第(3)小题的问题，所用到的思想方法与方法2差不多.因此，学生要学会用方法2独立求证此类问题.

图2

(1)略.

(2)设直线PA的斜率为k1，直线MA的斜率为k2，求k1k2的取值范围．

(2010年江苏省苏锡常镇一模数学试题)

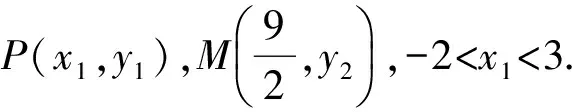
即

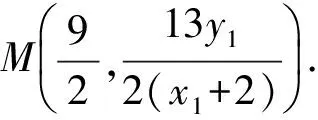
又因为

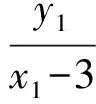
所以

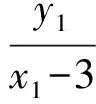
由点P在椭圆C上知

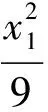
即

故

又

-2

从而

笔者总结:应用方程组求解点坐标是一种基本方法，但是当其中一个方程含参数时，一定要慎重考虑，计算较复杂.这时就凸显出“主动设点、引入多元”求解问题的优越性，这种技巧也称为“设而不解”，往往难在“如何消元”.

(1)略.

①求证：直线OA与OB的斜率之积为定值；

②求OA2+OB2．

(2011年江苏省南通市高三第三次数学调研试题)

(2)①证明设A(x1，y1)，B(x2，y2)，则

由点M在椭圆上，得

整理得

将式(4)和式(5)代入(注意到cosθsinθ≠0)，得

②解因为

所以

又

故

从而

注例2也只有少数学生能够独立求解完整，大部分学生无从下手，为什么？学生没有“主动设点、引入多元”求解问题的意识.事实上，只要能大胆设点尝试，一点不难.类似的问题还有：2009年福建省数学高考文科试题第22题，2011年江苏省淮安市第四次数学调研试题第17题，……

笔者在高三的2轮复习中，专题讲解了“解析几何中的多元问题”，但是从学生高考情况反馈来看，还是不够理想.中等水平学生告诉笔者：这是一个多元问题，教师专门讲过的，但是做得有点模糊.这说明专题讲解有效果，能让学生学会一种数学思想方法，今后将会用这些思想方法去尝试解决问题，从而具备更强的突破难题的能力.但是，仅仅有一个方向感是不够的，更需要学生具备灵活处理问题的动手能力.教师的讲解，无法取代学生的亲手尝试、切身感悟和自发反思.