简谈数学解题教学中的追问艺术
●(浙江师范大学2010级教育硕士 浙江金华 321004)●(新城中学 江苏无锡 214111)
简谈数学解题教学中的追问艺术
●章薇薇(浙江师范大学2010级教育硕士 浙江金华 321004)●浦叙德(新城中学 江苏无锡 214111)
提问是使用最普遍、最古老的教学方法之一,它是古希腊教育家苏格拉底著名的“产婆术”之核心.新课程认为,课堂教学是教师、学生、文本之间的对话过程,提问与回答是对话交流的主要途径.布鲁纳认为教学过程是一种持续不断地提出问题和解决问题的活动,思维永远是从问题开始的.当课堂提问后学生出现无法解决或回答不及本质时,教师应该根据学生答问所表现出来的问题再一次进行提问,这就是追问,显然,巧妙地运用追问可以解决学生认知和能力的不足.在数学课堂中,解题教学历来是重中之重,从某种程度上讲,它的成功就是数学课堂教学效能提高的有力保障.在解题教学中,巧妙的追问能促进学生进一步深入的思考与研究,问出问题源头、问出过程方法、问出数学本质.下面就数学解题教学中如何使用追问艺术谈一些看法,供读者参考.
1 云深不知处——投石问路巧追问
课堂提问应围绕着教学目标展开,解题教学中的数学题目必须在知识的重点、难点处设置,通过数学题目的解决过程来帮助学生扫清知识障碍,澄清模糊认识,提升思维水平.但在重点难点处设置的题目往往又不是每个学生都能轻易解决的.如果学生面对题目时,不能展开思考或根本无从下手,那么此时教师应通过投石问路巧追问,给思维不畅者以疏导,令其打开思路.
案例1小丽利用影长测量学校旗杆的高度.由于旗杆靠近一个建筑物,在某一时刻旗杆影子中的一部分映在建筑物的墙上.小丽测得旗杆AB在地面上的影长BC为40 m,在墙上的影长CD为4 m,同时又测得竖立于地面的0.5 m长的标杆影长为1 m,如图1所示,请帮助小丽求出旗杆的高度.

图1
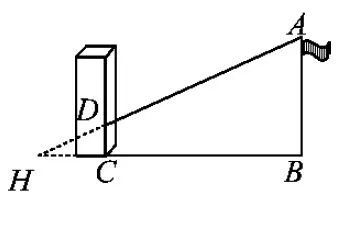
图2
面对这个题,大部分学生不知所措.
师(提问):这里的物高AB有影长吗?
生1:有,线段CB是AB的影长.
生2:不对,BC与CD都是AB的影长.
师(追问):那是不是BC+CD的长度就是AB的影长呢?
此处正是学生难以理解和处理的地方.让学生进行适当的讨论,有助于学生对该题本质的理解.
生3:CD+BC的长度不应该是AB的影长.如果AB足够短的话,它的影子就应该是BC,而正因为AB较长,所以一段影子在地上,一段在墙上.此时我们可以把墙上的影子CD看成新的物高,画出它的影长,即延长线段AD与线段BC交于点H,则HC为CD的影长(如图2)(得解法1,略).
生4:如图2,此时线段HB就是AB的影长(得解法2,略).
师(追问):线段CB能否看成某个物体的影子?
生5:过点D作DG∥BC,则DG是AG的影长(如图3)(得解法3,略).
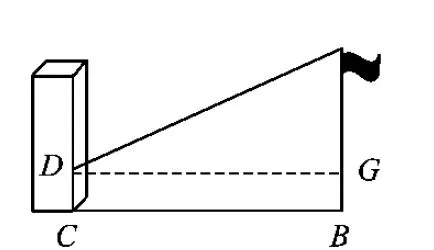
图3
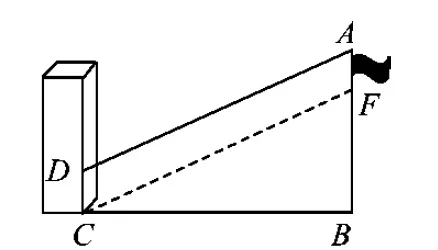
图4
生6:过点C作CF∥AD,则CB是BF的影长(如图4)(得解法4,略).
上述追问采用了顺向式追问,即顺着学生的思维追问,发现其思考的不足或错误后再次发问,引导学生深入思考,走上正确的思维轨道.
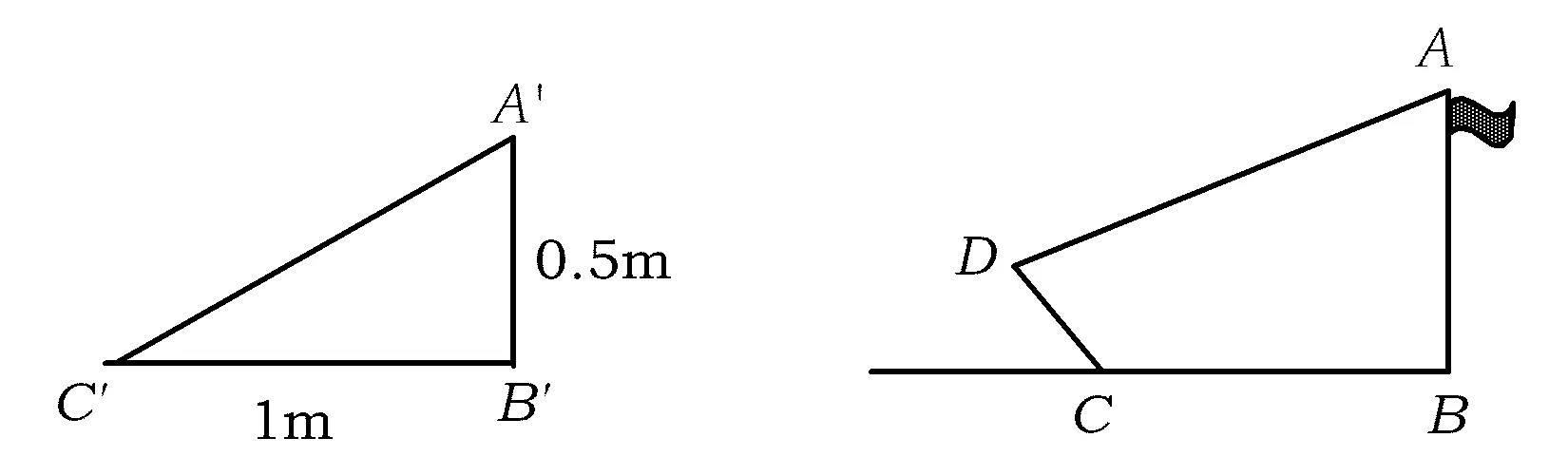
图5
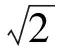
上述追问采用了顺势迁移式追问,即学生对基本问题掌握其数学本质后,顺势抛出类似的新问题,以此来激发学生更深层、更全面、更多元的思考,从而实现超越预设教学目标,完成思维的飞跃.
评注当学生思绪堵塞时,“投石”可以助其疏通思路;当学生思维欠缺深度时,“投石”可以给予适当的点拨;当学生思考没有方向时,“投石”可以给予引导与衔接.本案例中,通过教师投石问路巧追问,让学生从不同角度、不同方向、不同层次去思考问题,求同存异,使学生机智灵活地一题多解或多解一题,进而找到独特、巧妙的最佳方法,领悟问题的本质,课堂教学进入“课已终,题犹存,意更深”的意境.
2 润物细无声——去伪存真细追问
学生在解决数学题目的过程中难免会出现差错,作为教师不能简单粗暴地用一个“错”字打断学生的回答,然后越俎代庖地说出正确答案,而应充分利用错误资源中的有效信息,进行去伪存真细追问,在学生思维断层处进行正确思维的衔接,引导学生弄清产生错误的原因,并把握时机让学生揣摩正确的纠错方法,使之成为“美丽的错误,不小的收获”.
案例2判断:直线a上一点P到圆心O的距离等于半径R,则直线a与圆O相切.
生1:正确.因为它与切线的一个判定方法“与圆心的距离等于半径的直线是圆的切线”一致.
师(追问):“直线与圆心的距离等于半径”是什么意思?
意在让学生区分点与点之间的距离与点到线之间的距离.
生2:解释这里的距离是点到直线的距离.
师(追问):直线a上一点P到圆心O的距离等于半径R,是不是就直线与圆心的距离等于半径的意思?
此时学生的认知矛盾已得到化解.
师(追问):你能画出符合题意的反例示意图吗?
意在让学生能更深一步地找到自己错误的原因,从而扫除思维障碍.
评注在学生回答出错处、思维断层处进行追根溯源的追问,有利于促进知识的正迁移,进而让学生重新构建完整的知识体系,更深层次认识知识的本质所在.本案例中,教师以设问为抓手,抓住学生的认知冲突,通过去伪存真细追问,让学生认清相切是直线与圆的位置关系中的一种,通过点到直线距离的刻画,完成形数转换,其本质就是圆心到直线的距离等于圆的半径,使课堂教学达到“随问潜入思,润生细无声”的效果.
3 一览众山小——水到渠成妙追问
爱因斯坦曾经说过:“提出一个问题往往比解决一个问题更重要”.在解题教学过程中,教师应鼓励学生多角度思考问题,发表自己独特的思考与见解,教师应本着以人为本的理念,珍惜学生的异想天开,善待学生的惊人发现,并巧妙地利用追问引导学生从“设陷”与“避陷”中走出困境,获得真知.

图6
案例3如图6,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠EBA=45°.求证:CE·AB=2BD2.
采用实地勘测、线路调查、地形测量等方法,结合GPS技术的应用,对地形地貌变化、水系调整、植被破坏面积、损坏水土保持设施数量、水土流失面积等进行监测。
该题意在考查学生线段的倍半关系的解决方法.先将2BD转化成BC,并用三角形相似知识解决本题.
师(追问):本题还可以得到哪些正确结论?
学生探究得出以下结论:
(1)角度方面的结论:∠EBC=22.5°,∠ECB=67.5°,∠AEB=90°等;
(2)线段方面的结论:AE=BE,DE=BD=CD,AD⊥BC等;
有学生受到结论(3)的启示,提出了结论:AE=2DE.
师(追问):AE=2DE成立吗?你是怎么做出来的?
学生:若AE=2DE,则AE=BC=BE,而在直角△BCE中,BC≠BE.
学生通过“反证法”得出这个猜测是错误的.
这里采用的是逆向式追问,即逆着学生的思维或知识发生的过程追问,对学生已作出的正确回答给予肯定性评价后,反过来问理由,是对思考和理解过程的追问.
评注如果教师的解题教学始终停留在解完就结束问题的层面上,那么题海战术就永远不会消失.教师应充分利用学生获得的现有资源和思维成果及时进行总结、反思、拓展、延伸,使问题的价值获得最大化.本案例中,学生的思维是缜密的,思考是严谨的,但通过水到渠成妙追问,促使学生进一步交流与思考、类比与质疑、补充与完善,进而提出更深层面的规律与更广的结论.师生在表达和倾听、提问和追问中,收获的是“会当凌绝顶,一览众山小”的自信.
4 更上一层楼——意外拓展奇追问
叶澜曾经说过:“课堂应是向未知方向挺进的旅程,随时都有可能发现意外的通道和美丽的风景,而不是一切都必须遵循固定的路线而没有激情的行程.”是的,课堂教学是动态生成的过程,解题教学也不例外,随时会出现“意外”.如果我们能机智地为学生打破预设,并用睿智的追问,拓展学生思维,延伸思维空间,定会让解题教学中的“节外生枝”绽放出异彩.
案例4如图7,在菱形ABCD中,∠B=60°,点E,F分别从点B,D出发以同样的速度沿边BC,DC向点C运动,给出结论:(1)AE=AF;(2)∠CEF=∠CFE;(3)当点E,F分别为BC,DC的中点时,△AEF是等边三角形;(4)当点E,F分别为BC,DC的中点时,△AEF的面积最大.请判断上述4个结论的真假.

图7

图8
在解决了前面3个问题后,学生解决最后一问.
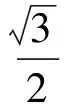
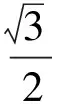
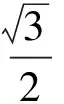

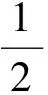
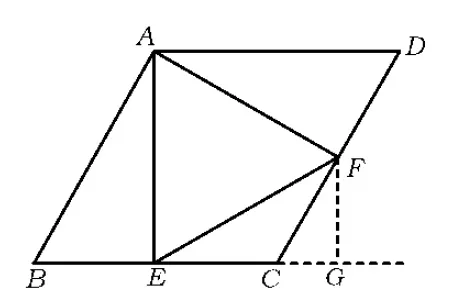
图9

图10
生2:这么做太麻烦了!如图9,设菱形边长为1,当E,F还没有动时,
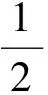
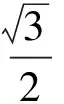
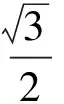

师(追问):我们用数量的大小关系说明了当点E,F分别为BC,EC的中点时,△AEF的面积不是最大值.如果不用数量说明,那么还可以从哪些方面入手呢?
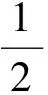
显然,如果没有及时而有效的追问,课堂中不曾预约的精彩是不会不期而至的.
评注解决一个有价值的数学问题往往是多途径的,而学生认识问题的角度也是多元的,他们会利用自己现有的显性知识和默会知识按自己的思考方式去解决问题,教师要做的就是正确的引导,使问题更趋向本质.本案例中,教师围绕问题从常规方法入手,先引导学生研究通法,但并没有浅尝辄止,而是充分利用课堂中的节外生枝,因势利导,通过意外拓展奇追问,从数到形层层抽丝剥茧,直至问题完美解决,课堂教学中呈现出“欲穷千里目,更上一层楼”的奇异之景.
可见,数学课堂教学中的追问是激活学生思维的点燃器,是引导学生走向理性的助长器,是课堂预设生成的催化器,是教学智慧形成的推进器.我们应在数学课堂教学中熟练掌握和运用追问,提高数学课堂教学的效能.同时,我们还应思考如何把教师的“课堂追问”转化为学生的“自我追问”,让学生在自我追问中不断反思,自主成长.只有这样,教学才会充满生机和活力,课堂才会实现教师和学生的同步发展.
[1] 浦叙德.浅谈数学课堂教学中的生成性追问及时机[J].中国数学教育(初中版),2011(5):2-4.
[2] 邵潇野.初中数学课堂提问的优化策略[J].中学数学教学参考(下半月·初中),2007(7):9-11.
[3] 温建红.数学课堂教学中的变式性提问与引申性提问[J].中学数学教学参考(中旬·初中),2010(1):17-19.

