巧构分布列 妙解数学题
●(锦屏高级中学 江苏连云港 222021)
巧构分布列妙解数学题
●殷长征(锦屏高级中学 江苏连云港 222021)
文献[1]中例6利用构造分布列求参变量的取值范围,简洁、流畅、巧妙.笔者读后有感,归纳出构造分布列可以速解(证)一些比较复杂的数学问题.现举例说明之.
1 证明不等式
例1设a,b,c∈R+,求证:

证明设事件ζ的分布列如表1所示.

表1 ζ的分布列
则
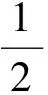
由Dζ=Eζ2-(Eζ)2≥0,得

例2已知ab=1 000,a>1,b>1,求证:

证明设事件ζ的分布列如表2所示.

表2 ζ的分布列
则


由Dζ=Eζ2-(Eζ)2≥0,得

因此

2 求最值
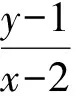
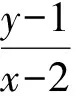
y=kx-2k+1,
代入方程(x+2)2+y2=1整理得
(x+2)2+(kx-2k+1)2=1.
设事件ζ的分布列如表3所示.

表3 ζ的分布列
则
Eζ=k(x+2)-(kx-2k+1)=4k-1,
Eζ2=k2+1.
由Dζ=Eζ2-(Eζ)2≥0,得
k2+1≥[k(x+2)-(kx-2k+1)]2=
(4k-1)2,
解得




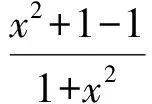
得
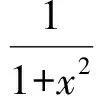
设事件ζ的分布列如表4所示.
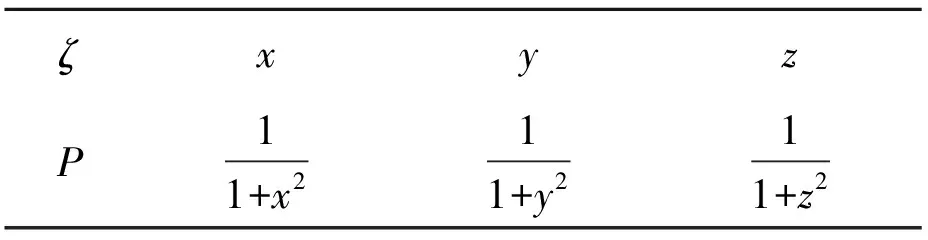
表4 ζ的分布列
则
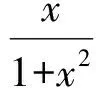

由Dζ=Eζ2-(Eζ)2≥0,得
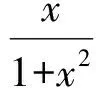
3 解方程(组)

解设事件ζ的分布列如表5所示.

表5 ζ的分布列
则

因为Eζ2=(Eζ)2,所以

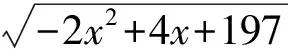
解得x=-7,经检验是原方程的根.
例6解方程组
解设事件ζ的分布列如表6所示.

表6 ζ的分布列
则

因为Eζ2=(Eζ)2,所以
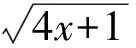
解得

4 求参变量的取值范围
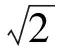
解设事件ζ的分布列如表7所示.

表7 ζ的分布列
则

由Dζ=Eζ2-(Eζ)2≥0,得

解得
a≥0或a≤-1.

解由1 994-x≥0且x-1 993≥0,得
1 993≤x≤1 994,
从而
y≥1.
设事件ζ的分布列如表8所示.
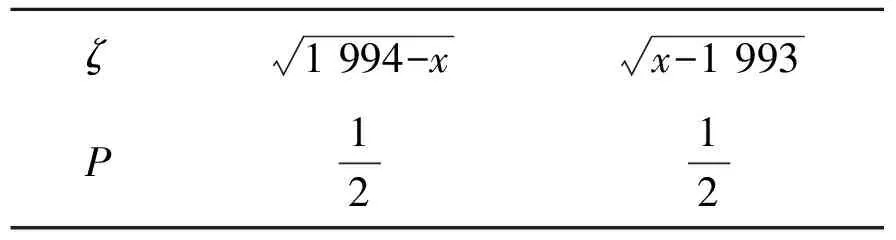
表8 ζ的分布列
则
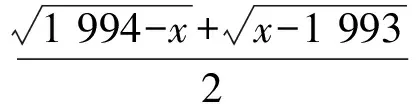

由Dζ=Eζ2-(Eζ)2≥0,得
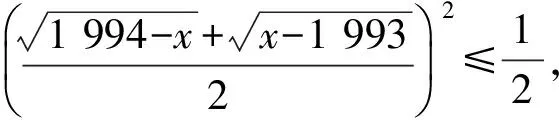
从而


点评以上解题的关键是巧设随机变量ζ的分布列,其主要思想有2点:(1)利用不等式的轮换性构造分布列;(2)利用“和为1”的条件构造分布列.
[1] 朱达峰.小构造 大作用[J].中学教研(数学),2011(4):9.

