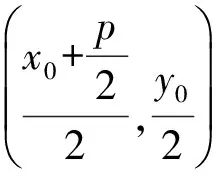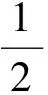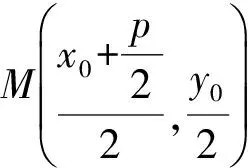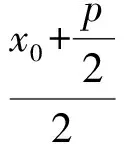从一道试题探究圆锥曲线的一组命题
●(盱眙中学 江苏淮安 211700)
从一道试题探究圆锥曲线的一组命题
●周志国(盱眙中学 江苏淮安 211700)
每年高考数学模拟试卷中都会出现新颖别致、个性鲜明、有一定难度的解析几何试题.2011年江苏省3所名校联考第18题是一道精彩的解析几何题目,给我们留下深刻的印象.笔者利用几何画板演示,对该试题进行探究,得到圆锥曲线的一组命题,以飨读者.
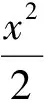
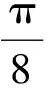
(2)当圆M与直线AF1相切时,求圆M的方程;
(3)求证:圆M总与某个定圆相切.
(2011年江苏省天一中学、海门中学、盐城中学联考试题)
分析(1)(2)略.
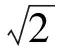
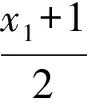
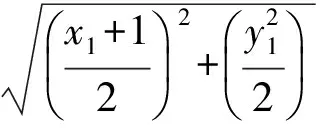
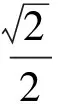
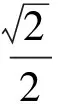
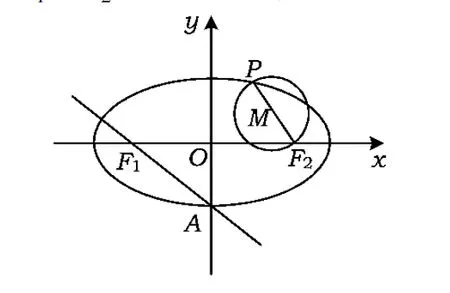
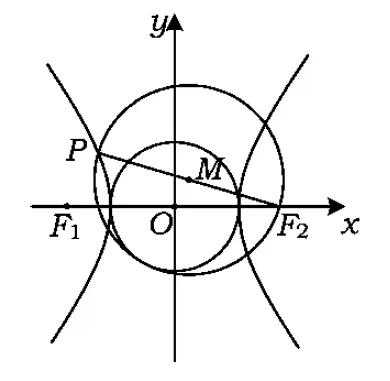
图1
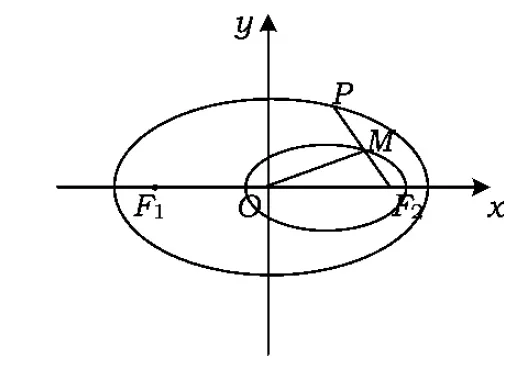
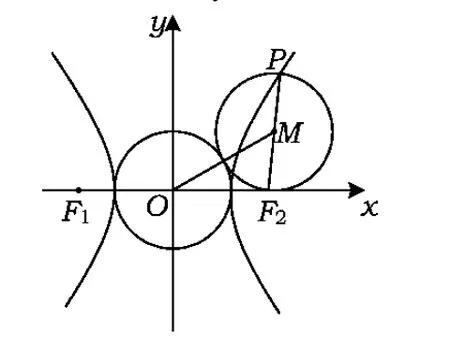
图2
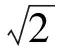

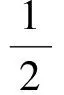
又因为P(x0,y0)在椭圆C上,所以
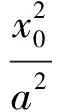

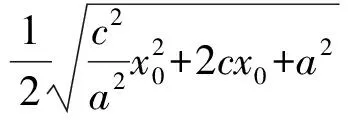
从而MO+MF2=a>c=OF2,故点M的轨迹是以O,F2为焦点的椭圆.

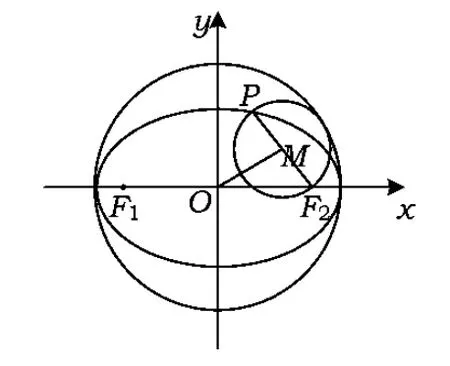
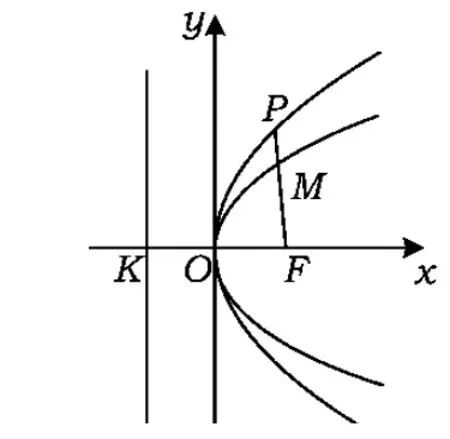
图3
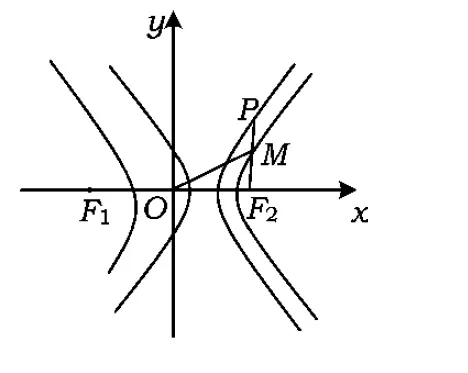
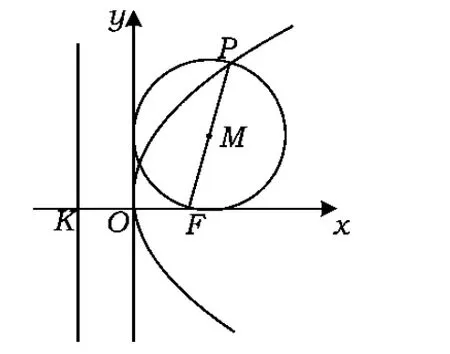
图4
证明由命题1的结论知M的轨迹是以O,F2为焦点的椭圆,且满足MO+MF2=a.而MF2=rM,a=r0,即MO+rM=r0,说明圆M总与定圆O:x2+y2=a2相内切,如图3所示.


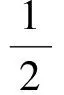
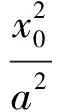
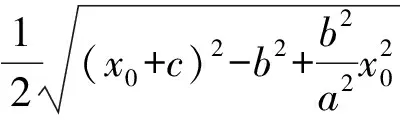
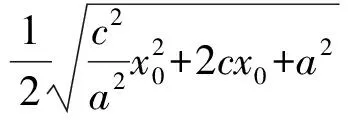
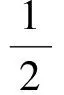
从而MO-MF2=a 综上所述,点M的轨迹是以O,F2为焦点的双曲线. 证明由命题2的结论知M的轨迹是以O,F2为焦点的双曲线. 当M是右支上的点时,满足MO-MF2=a,而MF2=rM,a=r0,得MO=r0+rM,说明圆M总与定圆O:x2+y2=a2相外切,如图5所示. 当M是左支上的点时,满足MF2-MO=a,而MF2=rM,a=r0,得MO=rM-r0,说明圆M总与定圆O:x2+y2=a2相内切,如图6所示. 综上所述,圆M总与定圆x2+y2=a2相切. 图5 图6 图7 图8 命题3已知抛物线C:y2=2px(p>0)的焦点为F,点P是抛物线上任意一点,点M是线段PF的中点,则点M的轨迹是以F为焦点的抛物线. 根据抛物线定义可知点M的轨迹是以F为焦点的抛物线,如图7所示. 推论3已知抛物线C:y2=2px(p>0)的焦点分别为F,点P是抛物线上任意一点,点M是线段PF的中点,圆M是以PF为直径的圆,则圆M总与定直线x=0相切. 证明由命题3,点M到y轴的距离为MF,而MF=rM,说明圆M总与定直线x=0相切,如图8. 以上探究揭示了圆锥曲线共有的一组性质,帮助我们进一步认清问题的本质,因此在平时的学习中要学会思考,通过数学实验(如几何画板演示)总结归纳出可能成立的一些命题,再通过代数推理给出证明.