一类代数无理不等式的深度探究

●(咸阳师范学院基础教育课程研究中心 陕西咸阳 712000)

一类代数无理不等式的深度探究

●安振平(咸阳师范学院基础教育课程研究中心 陕西咸阳 712000)

笔者曾在《数学通报》2003年第5期的问题栏目提出并证明了如下无理不等式：

问题1已知x,y为正实数，且n≥2(n∈N)，求证：

这是涉及2个正实数的无理不等式，且是开平方的情形.一种思考是:对开立方的情形如何呢？通过观察、尝试与探究，得到

问题2已知x,y为正实数，求证：

进一步的深度思考是：对开n次方的情形呢？关注分母里第2项的系数，容易得出

问题3已知x,y为正实数，且n≥2(n∈N)，求证：

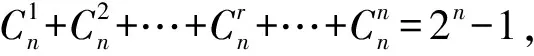
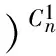
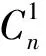
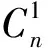
于是

变形得

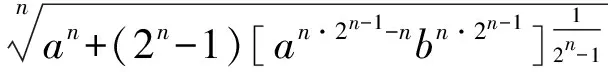
即

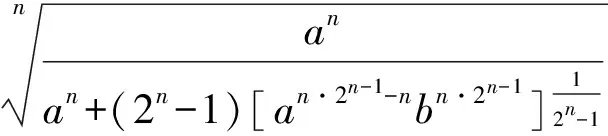
也就是

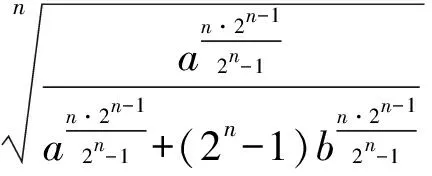
同理

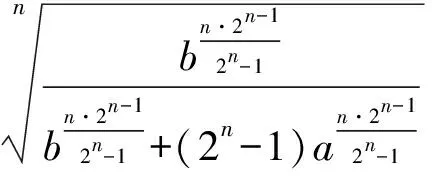
两式相加，得

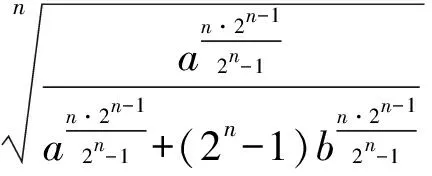
接下来的思考是，交换分母里系数2n-1的位置，会有类似的不等式吗？通过试验n=2，3等特殊值，笔者提出如下猜想：

问题4已知x,y为正实数，且n≥2(n∈N)，证明或否定：

需要提及的是，笔者在文献[1]里就曾得出：

已知：a>0,b>0，求证

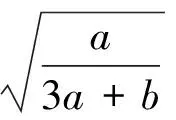
至于不等式(4)的证明，留给读者去思考.

(本文获得咸阳师范学院重点科研课题(08XSYK110)项目支持.)

[1] 安振平.一个数学问题的研究性学习[J].中学数学教学参考，2003(6)：43-44.

[2] 安振平，陈宝安.在阅读理解与思考变化中学习数学[J].数学通报，2008(7)：60-61.

[3] 罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，2008.