抛物线两弦端点处切线性质的进一步拓展
●(陕西电子工业学校 陕西宝鸡 721001)
抛物线两弦端点处切线性质的进一步拓展
●张东仓(陕西电子工业学校 陕西宝鸡 721001)
文献[1]中提到抛物线两弦端点处切线具有3个有趣的性质,笔者认为这3个性质还可以做进一步拓展,即对其作相应的修正,这样更能揭示抛物线的魅人之处!
文献[1]中定理1如下:
定理1如图1,设P是抛物线y2=2px(p>0)上任一点(除去顶点),弦PP1,PP2(或其延长线)分别过点M1(-m,0),M2(m,0),分别以P1,P2为切点的切线交于点P′,则点P在x轴上,且xPxP′=-m2.

图1
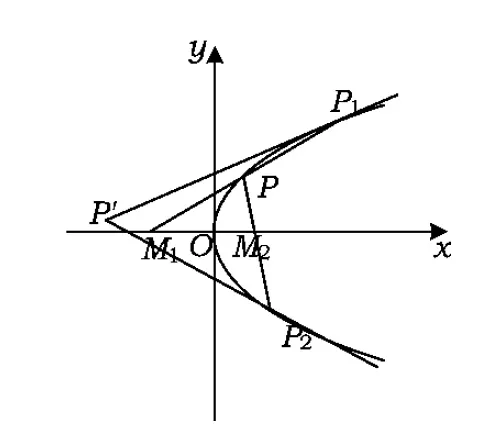
图2
笔者认为该定理中提到的点M1和M2关于原点对称,如果不对称,即经过抛物线上任意一点P的2条弦的端点P1,P2的切线交点P′还会在x轴上并且亦满足类似定理的结论吗?带着这样的思考,笔者对其进行了推证,发现文献[1]中提到的定理只是本文修正后定理的特殊情形而已.现对文献[1]中的3个定理做如下修正(不妨分别称为定理1′,2′,3′),并进行推证.
1 对文献[1]中定理1的修正
定理1′ 如图2,设P是抛物线y2=2px(p>0)上任一点(除去顶点),弦PP1,PP2(或其延长线)分别过点M1(c1,0),M2(c2,0),分别以P1,P2为切点的切线交于点P′,则P′满足
xP·xP′=c1·c2,yP·yP′=-p(c1+c2).
(很明显,当点M1与M2关于顶点对称时,c1与c2互为相反数,文献[1]中定理1自然成立.)
证明设P(x0,y0),P1(x1,y1),P2(x2,y2),则点P1,P2处的切线方程分别为
y1y=p(x+x1),y2y=p(x+x2),

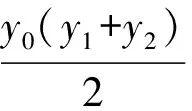
又点P,P1,M1共线,得

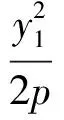
同理由P,P2,M2共线,得
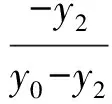

由式(1)与式(2),可得

xPxP′=c1c2,yPyP′=-p(c1+c2).
2 对文献[1]中定理2的修正

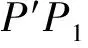
定理2′ 条件如定理1′,如图3,则
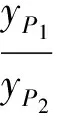
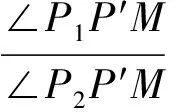
(点M为P1P2的中点);
(3)xP′=-xM′(点M′为P1P2与x轴的交点).
特别地,当P1P2恒过抛物线的焦点时,点P1,P2处的切线交点始终在抛物线的准线上.
很明显,当点M1与M2关于顶点对称时,c1与c2互为相反数,则yP1与yP2互为相反数,文献[1]中定理2自然成立.
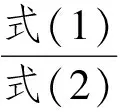

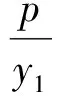
利用角公式可得

从而

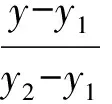

图3
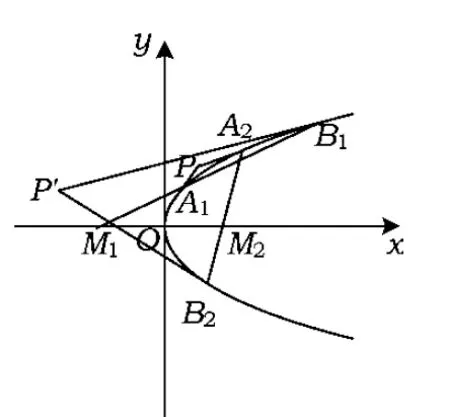
图4
3 对文献[1]中定理3的修正
文献[1]定理3如下:如图4,抛物线y2=2px(p>0)的2条弦A1B1与A2B2(或其延长线)分别过点M1(-m,0),M2(m,0).A1,A2处的切线交于点P,B1,B2处的切线交于点P′,则xP·xP′=-m2.与文献[1]中定理1,2的修正类似,现对文献[1]中定理3做如下修正,并进行推证.
定理3′ 抛物线y2=2px(p>0)的2条弦A1B1与A2B2(或其延长线)分别过点M1(c1,0),M2(c2,0).A1,A2处的切线交于点P,B1,B2处的切线交于点P′,则
xPxP′=c1c2.
(很明显,当点M1与M2关于顶点对称时,c1与c2互为相反数,文献[1]中定理3自然成立.)
证明设A1(xA1,yA1),B1(xB1,yB1),A2(xA2,yA2),B2(xB2,yB2).因为A1,B1,M1共线,所以

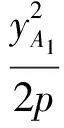
yA1yB1=-2pc1.
同理由A2,B2,M2共线可得
yA2yB2=-2pc2.
与定理1′证明类似,可知
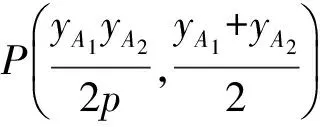
同理可得
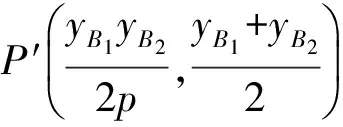
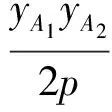
[1] 李青林,周园.抛物线两弦端点处切线的有趣性质[J].数学通讯,2008(23):21.

