小学数学学业水平测试与课程标准一致性水平探究*

● 刘学智 曹小旭

小学数学学业水平测试与课程标准一致性水平探究*

● 刘学智 曹小旭

借鉴韦伯模式，在分析县域小学数学学业水平测试与课程标准的一致性状况时发现，小学数学三年级一致性水平呈现出数与代数领域一致性水平最好，空间与图形领域次之，统计与概率领域一致性水平较差，而实践与综合运用领域一致性水平最差的特征。这说明我国学业水平测试存在偏离课程标准的问题，因此应采取有效策略，提高学业水平测试质量。

小学数学；学业水平测试；课程标准；一致性

学业水平测试是各县区教育行政部门监测学业质量的重要方法。课程改革的本质在于基于课程标准的教育改革，如何让学生学业成就评价建立在课程标准的基础之上，是国家、地方或学校实施基于标准的学业成就评价过程中必须解决的关键问题。[1]在实践中发现，各县区教育行政部门非常重视学生学业水平测试分数的解释，而忽视对学业水平测试是否反映课程标准要求的一致性推论，因而导致学业水平测试偏离课程标准的问题比较突山。本研究借鉴美国学者诺曼，韦伯(Norman．L．Webb)研制的学业评价与课程标准一致性的分析程序与方法(以下简称“一致性”)，即韦伯模式，对某县2010年小学3年级数学学业水平测试工具，即学业水平测试试卷进行一致性分析，为县区层面在实施学业质量监测过程中基于课程标准(以下简称“基于标准”)编制学业水平测试工具，提供必要的建议。

一、研究过程与方法

本研究以J省某县2010小学三年级数学学业水平测试试卷为监测对象。分析方法主要采用韦伯的一致性分析模式。韦伯分析模式是美国监测学业水平测试工具质量的重要方法。“近年来，韦伯模式已经成为理解学业评价和课程标准之间关系的最重要、最具有创新性的模式，目前该模式已经在美国24个州推广和应用。[2]本研究借鉴和改造韦伯一致性分析模式旨在对基于标准的小学数学学业水平测试质量进行监测与分析，即依据韦伯构建的一致性分析框架，从知识种类、知识深度、知识广度和知识分布平衡性等四个维度[3]，分析小学三年级数学一致性水平状况。

（一）确定编码“标准”

本研究采用数学课标中刻画的数学知识技能的目标动词为判定依据，即把了解、理解、掌握和灵活运用“四级”水平[4]，作为一致性数据的编码参照标准。

（二）选择编码者及编码

确定由课程专家、学科专家(小学数学骨干教师)、教研员三人组成编码小组。在共同编码过程中，不同类型的编码者分工明确，课程专家负责对课程标准的具体目标进行分析与解读，使编码小组成员很好地理解课程标准内容的难易程度。学科专家负责向编码小组提供课程实施中的学业评价状况，进一步辅助编码小组深刻理解评价项目。教研员集理论与实践知识于一身，在共同编码过程中，协调课程专家和学科专家在编码讨论过程中产生的分歧。本研究具体编码过程如下：编码小组依据了解、理解、掌握和灵活应用“四级”水平，对课程标准下的具体目标进行“水平等级”分析，在此基础上，对小学三年级数学学业水平测试的测验题目进行独立编码。

（三）数据整理

采用描述统计的方法生成知识种类、知识深度、知识广度和知识分布平衡性等“四维度”一致性可接受水平统计表。

（四）确定一致性可接受水平判定标准

表1 学业评价与课程标准一致性水平判断标准[5]

二、小学数学学业水平测试与课程标准一致性的基本状况

（一）一致性可接受水平状况分析

1．知识种类的一致性可接受水平

知识种类一致性是指用来判断评价项目涉及的学习内容范围与课程标准中描述的学习内容范围是否相一致。[6]表2显示，小学三年级数学学业水平测试试卷中数与代数、空间与图形、统计与概率、实践与综合应用四大学习领域的测验题目平均数分别为13、9．33、6．33、 0．33。按照表 1“击中领域目标的测验题目的平均数大于或等于6个题目即可判定知识种类达到一致性可接受水平。”的判断标准，数与代数、空间与图形、统计与概率三大学习领域其测验题目平均数均超过6个，因此我们有理由判定该三大学习领域知识种类均到达一致性可接受水平；而实践与综合运用领域击中领域目标的测验题目仅为0．33，其测验题目的平均数不足6个题目，由此可以判定该学习领域知识种类没有达到一致性可接受水平。

表2 知识种类一致性可接受水平统计表

2．知识深度的一致性可接受水平

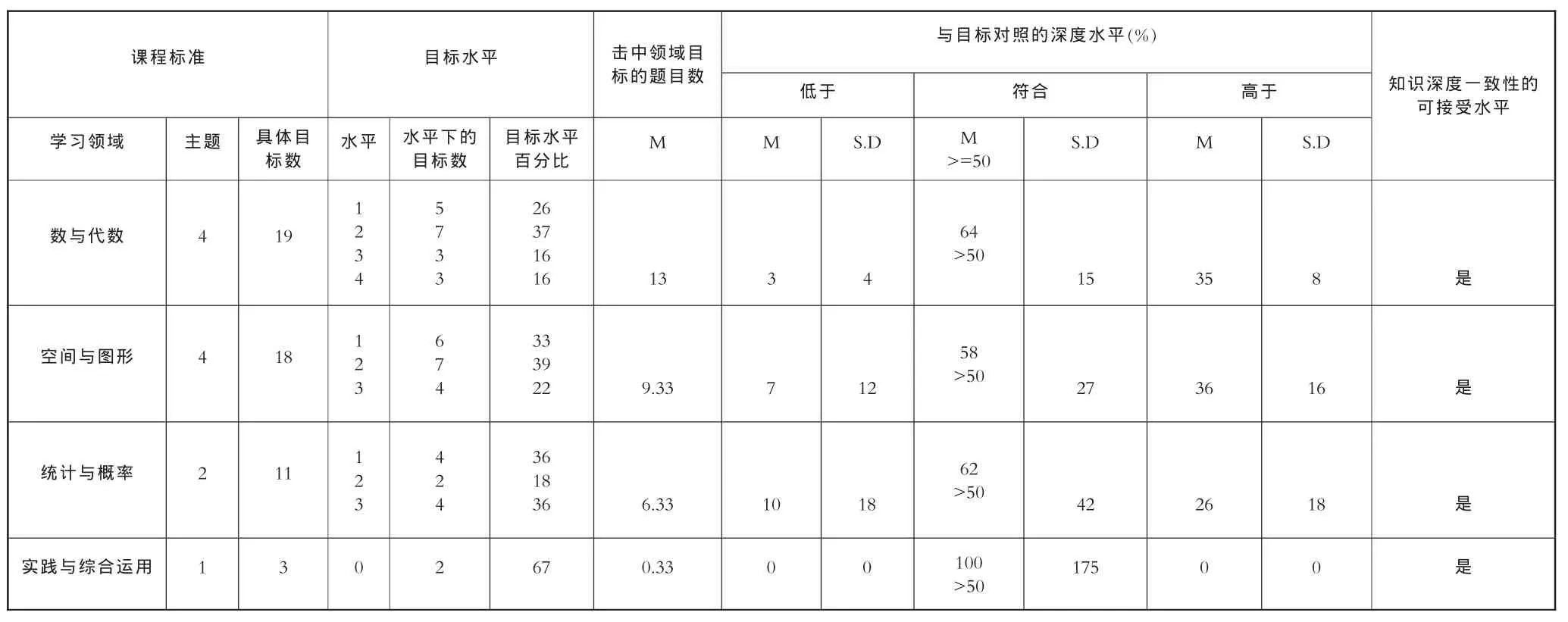
表3 知识深度一致性可接受水平统计表

知识深度一致性是指被用来判断所评价的知识技能、认知要求与课程标准中期望学生“应该知道什么”和“应当做什么”目标是否相一致。[7]表3显示，小学三年级数学学业水平测试试卷中数与代数、空间与图形、统计与概率、实践与综合应用等四大学习领域符合具体目标深度水平测验题目数百分比分别为64%、58%、62%、100%。按照表1“符合具体目标深度水平测验题目平均数的百分比大于或等于50%即可判定知识深度具有一致性”的判断标准，四大学习领域符合具体目标深度水平测验题目数的百分比均大于50%，因此我们有理由判定数与代数、空间与图形、统计与概率、实践与综合应用等四大学习领域知识深度都到达了一致性可接受水平。

3．知识广度的一致性可接受水平

表4 知识广度一致性可接受水平统计表

“知识广度一致性是指被用来判断课程标准中所涉及的概念、观点与学生为了正确回答评价项目所需要的概念、观点是否相一致。”[8]表4显示，数与代数、空间与图形、统计与概率、实践与综合应用等四大学习领域目标击中百分比分别为 58.1%、51．2%、38．8%、33．3%。按照表1“测验题目击中水平下目标数的平均数的百分比大于或等于50%即达到一致性可接受水平”的判断标准，四大学习领域仅有数与代数、空间几何达到可接受的一致性水平，而统计与概率、实践与综合应用等学习领域则难以达到知识广度一致性可接受标准。

4.知识分布平衡性的一致性水平

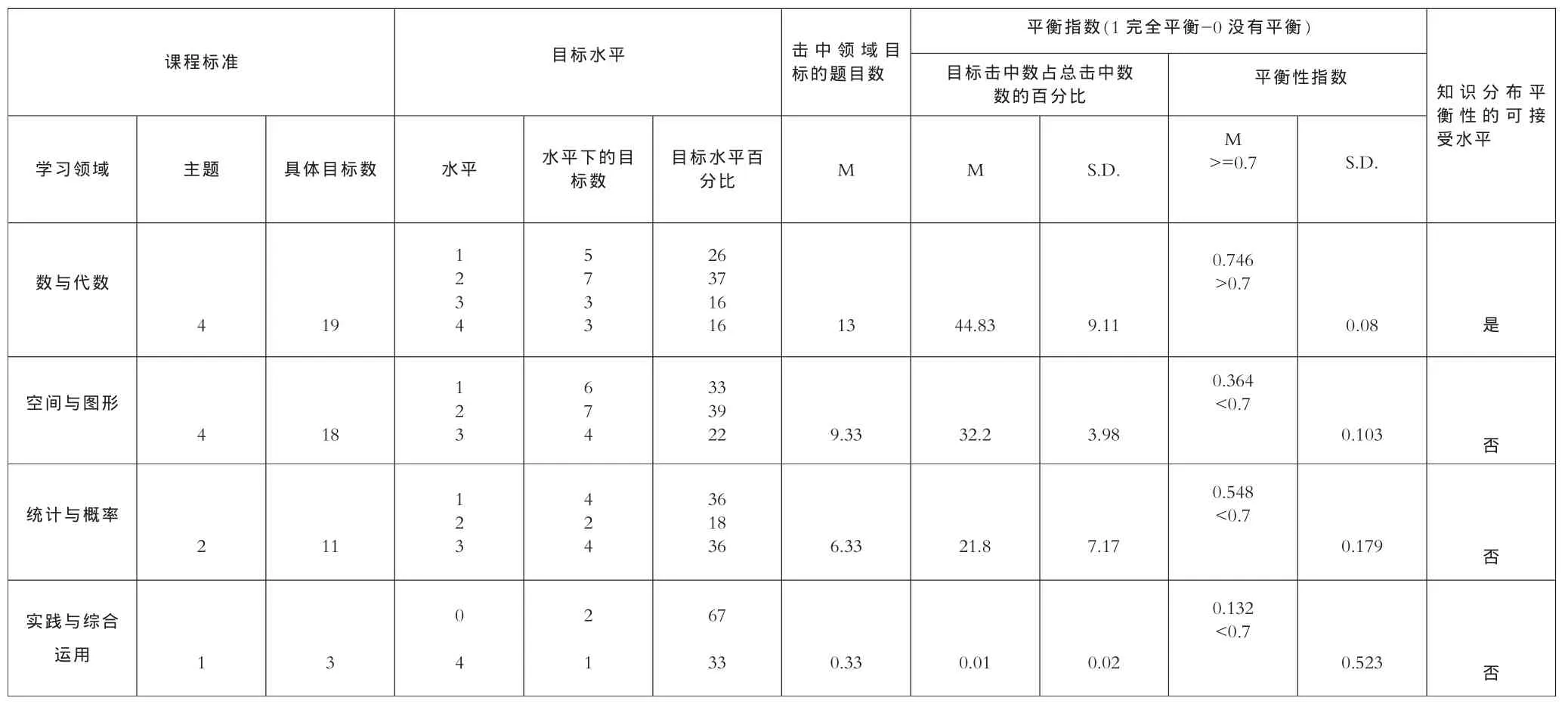
表5 知识分布平衡性可接受水平统计表

“知识分布平衡性是指考察评价项目在各项具体目标之间分布的均匀程度。”[9]表5显示，数与代数、间与图形、统计与概率、实践与综合应用等四大学习领域知识分布平衡性指数分别为 0.746、0.364、0.548、0.132。 按照表1当“知识分布平衡性指数的平均数大于或等于0.7，即达到一致性可接受水平”的判断标准”，该领域只有数与代数领域的知识分布平衡性达到了一致性可接受水平，其余各学习领域均未达到一致性可接受标准。

（二）研究结论与分析

探究小学数学知识种类、知识深度、知识广度和知识分布平衡性的一致性可接受水平状况，我们发现小学三年级数学学业水平测试与课程标准一致性水平具有如下特征：

l.数与代数领域一致性水平最好

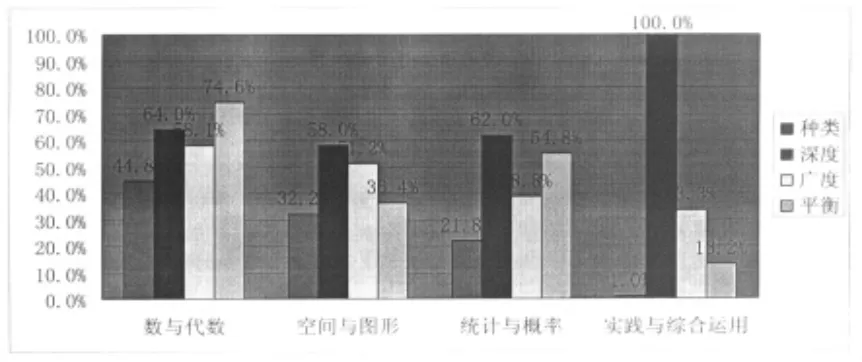
图1 小学三年级数学（上）学业评价与课程标准一致性总体水平统计图

从图1发现，在四大学习领域中，数与代数领域在四个维度上均达到指标要求，可以得出其一致性水平最好的结论。在小学阶段，数与代数是课程标准内容目标下的基本学习领域，是进一步学习其他数学知识的载体，同时，该领域在课程标准中所占内容比例大，所涵盖的知识点比较多，因而在编制试题时更倾向于数与代数领域，其一致性水平自然要好于其他领域。

2.空间与几何领域一致性水平较好

从图1发现，空间与几何领域前三个维度的一致性水平可以接受。该领域的测验题目直接体现了小学数学第一学段要求学生能够认识简单几何体以及平面图形，初步感受平移、旋转等现象，能够运用直尺等工具进行简单测量，与现实生活中儿童所接触到的各种实物有着密切的联系的内容，反映了数学课程标准关注学生生活实际的理念，因而一致性程度较好。

3．统计与概率领域一致性水平较差

从图1发现，统计与概率领域仅在知识种类及知识深度两个维度上的一致性水平可以接受，可见其一致性水平较低。数学课程标准中明确规定，统计与概率领域旨在帮助学生逐步建立起数据分析观念，了解随机现象及其发生概率以及可能性事件概念等，在现实社会中应用广泛。因此，从小学开始传授统计与概率知识具有极强的现实性和必要性。但由于该领域首次出现在新课标中，教师及试卷编制人员对其重视程度不高，进而在试卷编制时受到人为因素、检测时间、版面以及题型的影响及局限，很难把该领域更多的具体目标编排到需要考察的范围之内。

4.实践与综合运用领域一致性水平最差

从图1发现，实践与综合运用领域仅有知识深度一致性水平可以接受。该领域在试卷中测验项目只有一个题目，知识深度一致率为100%，说明该学习领域知识深度达到好的一致性水平。但除知识深度以外，其余维度均未达标，这说明该学习领域一致性水平仍然极差。实践活动是小学数学第一学段呈现的主要形式，课程标准中关于数学实践的目标旨在让学生在数学学习中经历观察、操作、推理等活动，了解数学在日常生活中的简单应用。这一部分对纸笔测验的要求较高，不易把握，因而在实际教学中，教师对这一领域的学业评价主要放在了课堂教学和日常学习生活中，而未将其作为纸笔测验内容。可见，试卷编制者对这一领域的领悟还不够深刻，未能很好的把握该领域的开放性、综合性等要求。

三、结语

本研究表明，J省某县小学三年级数学学业水平测试试卷具有数与代数领域一致性水平好于其他领域，空间与图形领域次之，统计与概率领域较差，而实践与综合运用领域一致性水平最差等特征。这表明，小学数学学业水平测试试卷的编制人员对数与代数和空间与图形领域的试卷内容把握比较好，而对统计与概率、实践与综合应用领域把握程度不够，存在偏离课程标准内容要求的问题。究其原因，在于我国数学课程标准中虽然明晰了内容标准，但却未能制定出科学严谨的学业评价标准，导致试题编制者在编制试题时无学业评价标准可依据。同时，以学业质量检测为目的的学业水平测试虽然具有一定的公平、公正性，但是避免不了会受到考试利害相关者的干预，比如试题编制者在编制试卷时要综合考虑来自学区或学校领导部门、教师以及家长的分数期望。各级领导受来自社会各方面的压力，不得不对课程编制施以权威影响；大多教师认为学习哪些知识就应该考察哪些知识，因而对教材中未能凸显，但在课程标准中却有所强调的某些具体目标不予理会；家长和学生对考试成绩的高期望，也会对试题的编制产生一定程度的影响，这些因素或多或少会导致试卷编制者在编制试卷内容时偏离课程标准的倾向。同时，各级教育部门过于重视对学生考试结果的监测与分析，而忽视对于学生学业水平测试工具质量的监测的做法，也会造成学业水平测试质量不高的问题，面对学业评价中的一系列问题，我们有必要借鉴韦伯等研究的一致性分析模式，创新具有本土化的学业水平测试质量监测方法，推动各地忠实于课程标准编制学业水平测试工具。

[1]崔允漷，王少非，夏雪梅．基于标准的学生学业成就评价[M].上海：华东师范大学出版社，2008，16．

[2]Council of Chief State School Officer(2006)Aligning Assessment To Guide The Learning of All the Students，45．

[3]Norman L．Webb．A1ignment of science and mathematics standards[M]．National lnstitute for Science Education University of WisconsinMadison，1999．11-18．

[4]中华人民共和国教育部．全日制义务教育数学课程标准(试验稿)[M]．北京：北京师范大学出版社， 2002．3.

[5]刘学智．小学数学学业评价与课程标准一致性的研究[D].(博士论文)．长春：东北师范大学教育科学学院，2008：64．

[6][7][8][9]刘学智.论评价与课程标准一致性的建构：美国的经验[J]．全球教育展望，2006(9)：36，36，37，37．

*教育部人文社会科学项目《学业评价与课堂教学一致性研究》（课题编号：09YJA880020）

刘学智/东北师范大学国际与比较教育研究所副教授，教育学博士，研究方向课程与教学论 曹小旭/东北师范大学国际与比较教育研究所硕士生，研究方向课程与教学论

（责任编辑：张 斌）