三正数可构成锐角三角形三边长的几个等价命题

● (广州大学附属中学 广东广州 510050)●

(华南师范大学数学科学学院 广东广州 510631)

三正数可构成锐角三角形三边长的几个等价命题

●郑慧娟(广州大学附属中学 广东广州 510050)●吴康

(华南师范大学数学科学学院 广东广州 510631)

熟知对任意正数a，b，c可构成三角形的等价条件为a+b>c，b+c>a，c+a>b.判定3个正数是否可作为三角形3条边的等价命题很多，例如：

正数a，b，c可构成三角形的等价条件有：

(2)2ab>|a2+b2+c2|；

本文对任意正数a，b，c能构成锐角三角形3条边长的等价条件进行探索，并得到了以下几个等价命题.

命题1正数a，b，c能构成锐角三角形3条边的充要条件是

(b2+c2-a2)(a2+c2-b2)(a2+b2-c2)>0.

(1)

证明必要性：在锐角△ABC中，设∠A,∠B,∠C所对的边分别为a，b，c，则

cosAcosBcosC>0,

代入余弦公式可得

(b2+c2-a2)(a2+c2-b2)(a2+b2-c2)>0.

充分性：若对正数a,b,c，则

(b2+c2-a2)(a2+c2-b2)(a2+b2-c2)>0，

即

b2+c2>a2,a2+c2>b2,a2+b2>c2.

否则b2+c2-a2,a2+c2-b2,a2+b2-c2中有2个为负数.不妨设b2+c2-a2<0，a2+c2-b2<0，相加可得2c2<0，产生矛盾.因此

同理可得

b+c>a，c+a>b,

从而正数a，b，c能构成三角形的3条边长.又由

命题2正数a，b，c能构成锐角三角形3条边长的充要条件是2a2b2>|a4+b4-c4|(或2b2c2>|b4+c4-a4|或2c2a2>|c4+a4-b4|).

证明由式(1)可得

(a2+b2+c2)(b2+c2-a)(a2+c2-b2)(a2+b2-c2)>0

⟺

[(a2+b2)2-c4)][c4-(a2-b2)2]>0

⟺

4a4b4-(a4+b4-c4)2>0

(2)

⟺

2a2b2>|a4+b4-c4|.

同理可得

2b2c2>|b4+c4-a4|，2c2a2>|c4+a4-b4|.

命题3正数a,b,c能构成锐角三角形3条边长的充要条件是

证明式(2)等价于

4a4b4-a8-b8-c8-2a4b6+2b4c4+2a4c4>0，

即

2(a4b4+b4c4+a4c4)>a8+b8+c8，

(4)

等价于

(a4+b4+c4)2>2(a8+b8+c8),

得

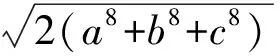
命题4正数a，b，c能构成锐角三角形3条边长的充要条件是

证明式(3)等价于

4(a4b4+b4c4+a4c4)>a8+b8+c8+2(a4b4+b4c4+a4c4),

即

4(a4b4+b4c4+a4c4)>(a4+b4+c4)2,

于是

[1] 苏化明.三正数可作为三角形三边的几个命题[J].中学教研(数学),1990(7)：21-22.