系统随机共振的最佳耦合矩阵

李义华,黄文静，李夏苗

(1.中南林业科技大学物流学院，中国 长沙 410004；2.长沙师范学校电子信息工程系，中国 长沙 410081；3.中南大学交通运输工程学院，中国 长沙 410075)

随机共振(Stochastic Resonance, SR)的概念最早出现在1981年，由意大利学者Benzi.R等人在研究地球古气象问题时提出[1-2]．随机共振是指非线性系统由弱周期驱动和随机力干扰相协作而导致强周期输出的现象．随着研究的深入，90年代，G.Hu等在文献[3]中指出单稳态无周期驱动系统也会有随机共振现象发生．对许多非线性系统来说，即使只有噪声的干扰，只要它具有一定的能量阀值和非对称性，随机共振现象也可能发生．在现代随机共振理论中，耦合振子系是最吸引人的研究对象之一，最初的结论由Benzi以及他的合作伙伴得出[4]．随后，Linder[5-6]提出了时空秩序和序列增强SR理论，并且把SR推广到两维空间．在上述研究中，人们发现SR的发生是周期驱动力、白噪声和系统耦合共同作用的结果．近年来，文献[7]对非线性耦合振子系进行了较为深入细致的研究，发现耦合振子系会发生比单个振子更强的随机共振效应，同时还会出现单个振子系中很难出现的现象．如果耦合矩阵不同，随机共振会有什么变化呢?本文对非线性Langevin方程的耦合进行研究，发现随着耦合矩阵的不同，系统能量变化也会不同，随机共振现象也会有所变化．利用遗传算法对最优耦合矩阵进行搜索，从而使得系统功率谱的谱峰达到最大值．

1 单个无周期驱动Langevin方程的随机共振

Langevin系统的确定性方程为：

(1)

由文献[8]知道，当01时，平衡点和阀值消失，粒子在圆周上作周期性的旋转运动．其中，S1表示一维空间，下同．

如果我们引入噪声，方程就成为单个无周期驱动的Langevin方程：

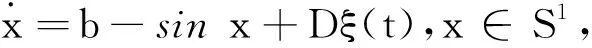
(2)

其中ξ(t)是Gaussian白噪声，满足：[ξ(t)]=0,[ξ(t)ξ(t′)]=δ(t-t′)．由于b-sinx的周期性，方程(2)可看成一个阻尼粒子在圆周上受到常驱动力和随机力共同作用的运动方程．当b≤1时，系统(2)会发生随机共振．

2 N个无周期驱动一阶Langevin方程的耦合

下面来看N个Langevin方程耦合的情况，方程如下：

(3)

其中bi≥0是第i个振子受到的常驱动力，K>0是耦合系数，D为噪声强度，ξi(t) 是Gaussian白噪声，满足[ξi(t)]=0,[ξi(t)ξi′(t′)]=δii′(t-t′)，相互作用矩阵为：

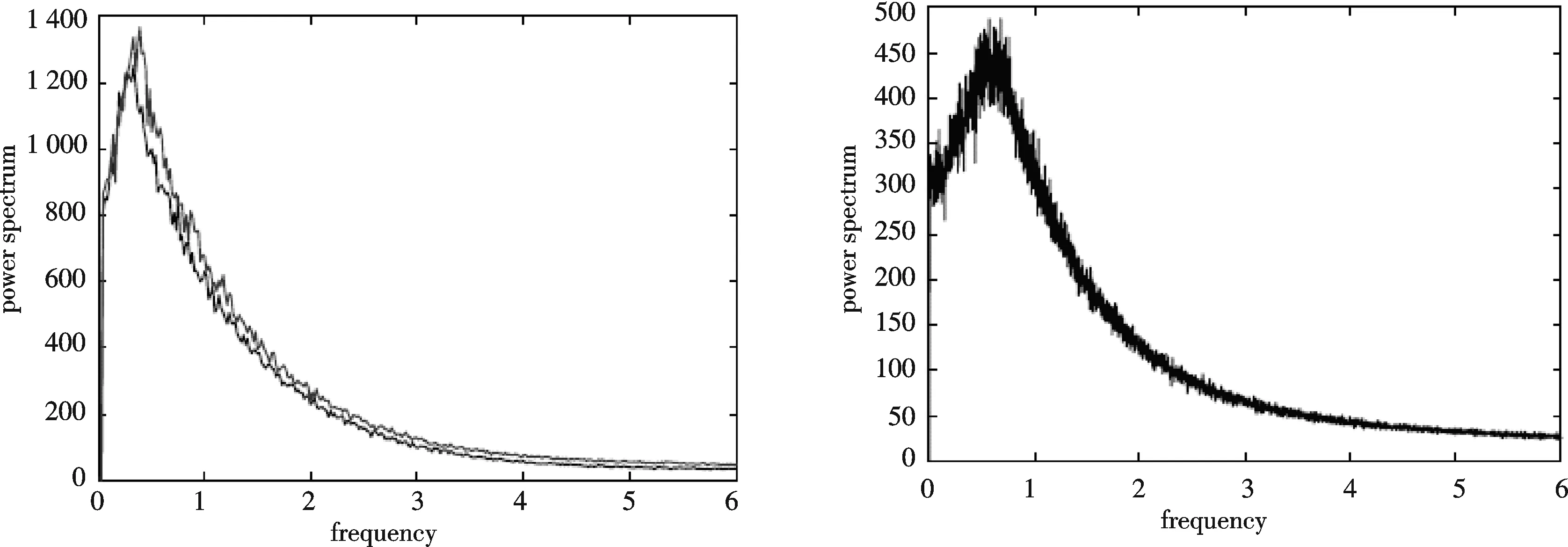
图1 左图：K=0.5,K=1时不同相互作用矩阵对应的功率谱图，右图：K=0时单个振子的功率谱图

如果变化系统(3)的相互作用σ矩阵，可以看到，随着相互作用矩阵不同，功率谱的高度和宽度都有相应变化，进一步的数值模拟发现：相互作用矩阵中各个元素的值相差不多时的功率谱高度比矩阵中各个元素差别较大时的高度要小，并且矩阵中各个元素值不能取得太大，否则影响噪声在系统中的作用．

接下来，假设相互作用σ矩阵分别服从均匀分布、Γ分布、正态分布3种不同的概率分布，然后分别求出它们相应的功率谱．发现矩阵元素服从不同分布的σ矩阵，功率谱高度和宽度都有相应的变化．即使是服从同一分布的σ矩阵，功率谱高度和宽度也会随着矩阵元素的不同而有相应的变化．为了比较3种分布中哪一种概率分布最优，把Γ分布的两个参数μ、υ放到平面坐标中，μ为横坐标，υ为纵坐标，分别在横纵坐标上从1个单位开始取10个点，每个点之间长度为1，这样就得到平面上100个坐标点，将每个点的(x,y)取值作为Γ分布的两个参数，再求这100个Γ分布对应功率谱的平均值，得到一个平均功率谱图．同样对均匀分布、正态分布求平均，也可以得到它们相应的平均功率谱图．

可以看到，σ矩阵中元素服从均匀分布谱峰高度最高，宽度最窄；当σ矩阵中元素服从Γ分布谱峰高度最低，宽度最大．实验过程中的数据显示，在均值和方差相同的情况下，服从均匀分布的矩阵元素相差很小，然而服从正态和Γ分布的矩阵元素之间相差较大，后两个分布使得系统共振的效果要好很多，所以谱峰高度比服从均匀分布高很多，其中服从Γ分布的矩阵元素差别最明显，使得谱峰高度最高，宽度最窄．因此，不同的矩阵对系统能量输出有着明显的影响．

3 利用遗传算法搜索最优耦合矩阵

遗传算法(Genetic Algorithm，简称GA)是以自然选择和遗传理论为基础，将生物进化过程中适者生存的规则与群体内部染色体的随机信息交换机制相结合的高效全局寻优搜索算法，由美国Michigan大学的J.Holland教授于1975年首次提出，现已发展成为一种实用、高效、鲁棒性强的优化技术，它的运算流程如下：

(1)编码；(2)初始群体的生成；(3)适应度值评价检测；(4)选择；(5)交叉；(6)变异：群体P(t)经过选择、交叉、变异运算后得到下一代群体P(t-1)； (7)终止条件判断：若t≤T，则转到步骤(2)；若t>T，则以进化过程中所得到的具有最大适应度的个体作为最优解输出，终止运算．

为了找到最优相互作用σ矩阵，使功率谱波峰达到最高点，我们采用遗传算法对3×3,5×5相互作用σ矩阵进行最优值搜索．搜索过程中，设定求功率谱谱峰值的函数为目标函数，Q矩阵中除对角线以外的各个元素为目标函数的变量．因为矩阵中元素太大会影响噪声在系统中的作用，所以把目标函数的变量控制在[0,1]之间．在求系统(2)的动力解时，采用迭代法，迭代215次，根据遍历性，足够让系统最后处于一个非常稳定的状态．但是，由于计算机采用的是精度计算，让目标函数对同一组变量所得的值有很小的差别，这就使得遗传算法不能收敛到某一个固定值，而是围绕某个值的周围上下波动，所以搜索到的最优σ矩阵与波峰值都是一种近似值，结果如下：

i)3×3矩阵，将矩阵元素控制在[0,1]之间，遗传200代后，搜索到的波峰值如图2所示．

图2 左图： 3×3耦合矩阵在200代遗传中每代最优解以及解的均值；右图：遗传算法搜索到的3×3最优耦合矩阵的功率谱图

搜索到的最优矩阵为

它对应的功率谱图如图2右图，波峰值为3.552 199′79′735 525 0e+003．它的第一、二特征值分别是0.000 003 5和-0.169，正定．把最优矩阵分别与任意3个矩阵相加，得到新的矩阵对应的功率谱图．可以看出，新矩阵的功率谱的高度小很多，并且波峰宽度明显大些．所以，系统的能量输出远不如最优矩阵．同时，任意选了3个矩阵，画出它们对应的功率谱图，可以发现，跟最优矩阵的功率谱图相比较，波峰的高度和宽度都远没有最优矩阵的理想．所以，最优矩阵让系统产生了共振，使得系统的输出能量达到最高．为了找出耦合矩阵与功率谱最大值之间的关系，计算出6个任意选择的矩阵的第一、第二特征值，将除0以外的各个矩阵的第二特征值(即第二大的特征值)进行比较，可以看出，随着矩阵第二特征值的变化，功率谱最大值也相应地发生变化，并且功率谱波峰值大的，耦合矩阵的第二特征值就较大，如图4左图．因此，耦合矩阵的第二特征值与波峰值有一定的联系．

ii)5×5矩阵，也是将矩阵元素控制在[0,1]之间，遗传450代后，搜索到波峰值如图3所示.搜索到的最优矩阵为

它对应的功率谱图如图3右图，波峰值为3.688 194 631 425 216e+003．它的第一、二特征值分别是-0.000 001和-0.064．

图3 左图：5×5耦合矩阵在450代遗传中每代最优解以及解的均值；右图：遗传算法搜索到的5×5最优耦合矩阵的功率谱图

类似3×3矩阵，拿最优矩阵分别与任意3个矩阵相加，得到新的矩阵对应的功率谱图，可以看出，新矩阵的功率谱的高度小很多，并且波峰宽度明显大些，所以，系统的能量输出远不如最优矩阵．同时，我们任意选了3个矩阵，画出它们对应的功率谱图，可以发现，跟最优矩阵的功率谱图比起来，波峰的高度和宽度都远没有最优矩阵的理想，所以，最优矩阵让系统产生了共振现象，使得系统的输出能量达到最高．可以看出，正如前面所说，矩阵中的元素有差别时功率谱的高度和宽度更加理想，并且系统能量输出能达到最大，最大值都在3 500左右．为了找出耦合矩阵与功率谱最大值之间的关系，我们计算出6个任意选择的矩阵的第一、第二特征值，将除0以外的各个矩阵的第二特征值进行比较，如图4右图，可以看出，随着矩阵第二特征值的变化，功率谱最大值也相应的发生变化，并且功率谱波峰值大的，耦合矩阵的第二特征值也较大．因此，耦合矩阵的第二特征值与波峰值有一定的联系．

图4 最优矩阵与任选矩阵第二特征值的比较.左图：A坐标代表任意选出来的6个3×3σ矩阵或5×5σ矩阵与最优矩阵的序列(其中左图中序列4为最优矩阵，右图中序列6为最优矩阵). D坐标代表对应矩阵的第二特征值

4 结语

本文主要讨论了系统经过耦合后在噪声作用下发生的随机共振现象．随着耦合矩阵的不同，系统的能量输出也相应地发生着变化．本文利用遗传算法搜索到最优耦合矩阵，使得系统能量输出达到最大值，这让我们对随机共振有了更加深入的了解．随机共振现象处处都存在，近年来，对随机共振现象的发生及相应机制的研究受到各个领域科学家们越来越多的关注，增进对它的了解，可以帮助我们更好地控制系统能量输出与微小机制的运作．

参考文献：

[1] BENZI R, SUTERA A, VULPIANI A. The mechanism of stochastic resonance[J]. J Phys, 1981, A14(7)：453-462.

[2] BENZI R, PARISI G, SUTERA A,etal. Stochastic resonance in climatic-change[J]. Tellus, 1982, 34 (10)：112-123.

[3] PANKRATO A L, SALERNO M. Acliabatic approximation and parametric stochastic resonance in a bistable system with periodically driven barrier[J]. Phys Rev, 2000, E61(5)：1206-1215.

[4] BENZI R, SUTERA A, VULPIANI A. Stochastic resonance in the landau-ginzburg equation[J]. J Phys, 1985, A18(9): 2239-2243.

[5] LINDNER J, MEADOWS B K, DITTO W L,etal. Array enhanced stochastic resonance and spatiotemporal synchronization[J]. Phys Rev, 1995, 75(3)：1005-1011.

[6] LINDNER J F, MEADOWS B K, DITTO W L,etal. Scaling laws for spatiotemporal synchronization and array enhanced stochastic resonance[J]. Phys Rev E, 1996, 53(1)：2081-2092.

[7] 张雪娟. 双稳态系统-单稳态系统-耦合振子系和混沌系统的随机共振现象[D].北京：北京大学博士论文，2002.