时间序列搜索问题的在线决策算法
张瑞英,张远平
(兰州理工大学计算机与通信学院,中国 兰州 730050)
随着在线算法的深入研究,在线决策问题已经成为一个热点研究问题.在线决策问题是研究不完全信息下的决策问题,即输入总是逐步被提供,对于每个输入部分,在线算法需要在不知道以后信息的情况下给出输出.由于不可能知道和预测未来的确切信息,因此往往无法对问题做出最优决策,而只能尽量给出问题的满意决策.而本文研究的时间序列搜索问题是现实中一个典型的在线决策问题,决策算法性能由竞争比决定,即决策结果与离线最优决策结果的某一比值[1-2].
最初的时间序列搜索模型是由El-Yaniv等建立的[3].El-Yaniv等研究了已知价格在区间[m,M]波动的时间周期为n的时间序列搜索问题,提出了保留价格的确定性算法和基于风险的随机性算法,并分析证明了算法的竞争比[4].1999年Al-Binali在此基础上对该问题做了进一步研究,依据在线者对未来的预期和所能承受的风险来确定出一个在线策略集合,而后根据预期成功后最小的约束竞争比来选择在此模型下的最优在线策略[5].Lorenz等研究了k最大序列搜索问题和k最小序列搜索问题,提出了相应的确定性算法和随机性算法,并运用最坏情况分析计算了算法的竞争比[6].Damaschke等研究了价格上下界限随着时间以一种特定方式变化的时间序列搜索问题,提出了最优确定性算法和近似最优随机性算法[7].Xu等通过引入利润函数对最初的时间序列搜索模型进行了扩展,然后运用最大最小定理提出了已知时间周期的确定性算法(Algorithm with Known Duration,简写为AKD)[8].
与时间序列搜索问题紧密相关联的问题是单向交易问题,El-Yaniv等在文献[4]中指出任意的确定性单向交易算法都可以看作随机性时间序列搜索算法.2009年,Fujiwara等对单向交易问题进行了平均情况竞争比分析,基于最大汇率服从一个已知分布的假设,采取不同的最优化标准得出了相应的最优化策略[9].2004年,Kakade等在单向交易模型基础上引入了量的概念,研究了量权平均价格交易和受限订单交易[10].
本文是在Xu研究的模型[8]基础上提出了随机性决策算法RAKD(Random Algorithm with Known Duration),并分析证明了其竞争比,最后通过实验与确定性算法进行了算法性能比较,分析及实验结果表明该算法可以在一定情况下降低算法竞争比.另外El-Yaniv等人研究的时间序列搜索问题模型[4]因为没有引入利润函数,因此应用具有一定的局限性,而与其相比,本文研究的时间序列搜索算法应用范围较为广泛.
1 基本模型及概念
基本模型:一个在线者在一个报价序列中选择且只能选择一个价格,目的是在兑换货币1为货币2时最大化地获得利润.给定n个不相交的时间段,每个时间段称为一个时间周期.在第i(i=1,2,…,n)个时间周期,在线者获得一个报价pi,然后必须立刻决定是否要在这个时间周期接受该价格,一旦在线者接受了价格pi,则交易结束,在线者获得的利润为fi(pi),即第i时间周期接受价格pi的利润.否则pi无效,pi+1在下一个时间周期到达.
对于本文研究的在线时间序列搜索问题,有以下3个基本假设
(1) 价格在区间[m,M],在线者预先知道n,m,M的值以及利润函数f的表达式.
(2) 利润函数f是连续的且是价格p的递增函数.
(3) 对于任意的汇率p∈[m,M],f1(p)≥f2(p)≥…≥fn(p) .
在假设(1)中,如果n=1,则在线和离线情况下,在线者只能接受唯一的一个价格,因此在线和离线情况下,在线者会获得同样的利润,所以在后面的分析中我们只考虑n≥2的情况.假设(2)和(3)说明在每一个时间周期,较大的价格对应大的利润,对于每一个价格,早期接受获得的利润高于在后期接受获得的的利润.并且注意到在上述模型中如果fi+1(M)≤fi(m)在某一时间周期i成立,则在线者肯定会在时间周期i或i之前接受一个价格并结束交易,这是因为对于任意k
另外为了后面叙述清晰,先定义如下符号:
pi——第i个时间周期的价格,
fi(pi)——第i个时间周期对于给定的价格pi所获得的利润,
Si——第i个时间周期交易的货币1的数目,
Di——第i个时间周期交易后,在线者仍拥有的货币1的数目.由定义可知:Di=Di-1-Si,并定义D0=1表示在未进行交易时在线交易者拥有的货币1的初始值为1.
Yi——第i个时间周期交易后,在线者拥有的货币2的数目,由定义可知:Yi=Yi-1+Sifi(pi),并定义Y0=0表示在未进行交易时在线交易者拥有的货币2的初始值为0.
2 随机性决策算法
Xu 等对于上述模型运用最大最小定理提出了确定性算法AKD,其竞争比r为[8]:
本文运用基于风险的思想提出了随机性算法RAKD,分析其竞争比,并通过实验和确定性算法进行了对比,其中算法思想如下:
规则1只有当前的价格汇率用利润函数计算后的值为迄今最大的时候才考虑将部分货币1兑换成货币2.
规则2每次将货币1兑换为货币2时,我们只兑换最少数目的货币1,使得即使以后的价格汇率一直保持最低时我们仍能保证竞争比为r.
与AKD相比较,这两个规则表明随机性算法RAKD不是一次性的完成交易,是每次兑换剩余货币1的一部分,而AKD则是接受唯一的价格一次性兑换所有的货币1.
注意,这两个规则应用于除最后一个时间周期的所有其他时间周期,因为按照问题的表述,在线者必须在最后一个时间周期交易所有剩余货币1为货币2,并且只有当当前价格汇率经利润函数计算后最大时才交易,所以假设:
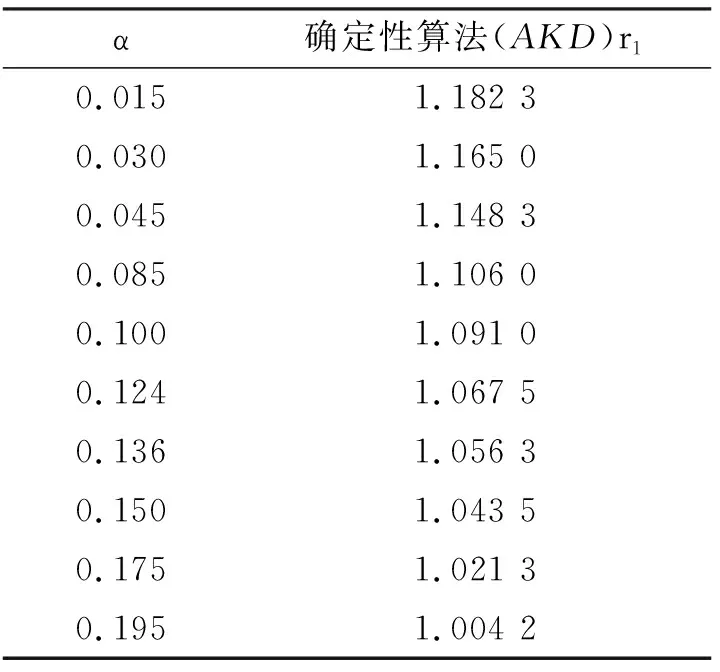
rfn(m)≤f1(p1) 根据随机性决策算法的思想及最坏情形分析,有如下引理成立. 证由于RAKD的竞争比是r,根据规则2, 由Di和Yi的定义,有 因为RAKD必须兑换满足上述不等式的最少数目的货币1,可以看出上述不等式左边是关于Si的递减函数,因此替换不等式为等式,解关于Si的方程,得到 (1) (2) 证毕. 解关于r的方程得到r的表达式为 进而可得到如下等式 为了计算出竞争比r的最大值,我们需要找到上式后半部分的最大值.令Xi=fi(pi)-fn(m),则 此时,r只与f1(p1)和fk(pk)有关,即只与p1、pk及k有关. 于是可以解得对于2 (3) 证令t=f1(p1),且有如下的替换 r(k,p1)对t求导,可以得到 考虑上式的分子,对于任意的v和k>1,方程 uk+fn(m)ku-fn(m)(k-1)v=0. (4) 代入到(3)式,可以证明引理2,即 证毕. 证由上面的讨论可知,r最大时对于任意的1 S2=S3=…=Sk, 且由(1)式和引理2有 该定理可通过(3)式,引理2,函数f的性质及单调性推导得出. 另外需要注意的是在实际应用中,如果在第i个时间周期,在线者获得的价格汇率pi偏离了最坏情况序列,则在线者可以计算出以该汇率pi为第1个时间周期,在剩余n-i个交易周期的最优竞争比r′,并用该竞争比r′决定在第i个时间周期要兑换的货币1的数目. 观察表1,可知随着参数α的递增,确定性算法的竞争比r1逐渐递减.而根据定理1计算得出,在最坏情况下,随机性算法(RAKD)的竞争比r2将保持为1.067 5不变.我们看到由于随机性算法扩大了在线最坏情况序列的利润,因此得到的竞争比不一定比确定性算法的竞争比小,所以对于上述的利润函数得出如下的结论:当0<α≤0.124时,采用随机性算法,当0.124<α<0.2时,采用确定性算法.并通过上述实验可知,随机性算法在一定情况下实现了算法竞争比的降低. 表1 竞争比结果(M=120,m=100,n=30) 本文在文献[8]的模型基础上提出了基于风险的随机性决策算法,分析证明了随机性算法的竞争比,并通过实验表明这一算法使得时间序列搜索问题的竞争比在一定情况下得到降低.在实际应用中,将根据具体的利润函数决定采取确定性算法或随机性算法.并且引入利润函数的时间序列搜索模型是El-Yaniv等人[4]提出的问题模型的一般化,因此应用范围较为广泛.另外,对于时间序列搜索问题的确定性算法和随机性算法的平均情况竞争比分析将是今后值得研究的问题. 参考文献: [1] BORODIN A, EL-YANIV R. Online computation and competitive analysis[M].Britain:Cambridge University press,1998. [2] SLEATOR D D, TARJAN R E. Amortized efficiency of list update and paging rules [J]. Comm ACM, 1985, 28(2):202-208. [3] EL-YANIV R, FIAT A, KARP R M,etal. Competitive analysis of financial games:proceedings of 33rd Annual Symposium on Foundations of Computer Science, Pittsburgh, PA, USA, 1992[C]. Pittsburgh:USA, 1992. [4] EL-YANIV R, FIAT A, KARP R M,etal.Optimal search and one-way trading online algorithms[J]. Algorithmica,2001,30(1):101-139. [5] AL-BINALI S. A risk-reward framework for the competitive analysis of financial games[J].Algorithmica,1999,25(1):99-115. [6] LORENZ J, PANAGIOTOU K, STEGER A. Optimal algorithms for k-search with application in option pricing[J].Algorithmica,2008,55(2):311-328. [7] DAMASCHKE P, HA P H, TSIGAS P. Online search with time varying price bounds[J]. Algorithmica,2007,55(4):619-642. [8] XU Y, ZHANG W, ZHENG F. Optimal algorithms for the online time series search problem[J]. Theor Comput Sci,2009,doi:10.1016/j.tcs.2009.09.026. [9] FUJIWARA H, IWAMA K, SEKIGUCHI Y. Average-case competitive analyses for one-way trading [J].J Comb Optim,2009,(published online). [10] KAKADE S M, KEARNS M, MANSOUR Y,etal. Competitive algorithms for VWAP and limit order trading:EC′04 proceedings of the 5th ACM conference on electronic commerce, ACM, New York, NY, USA, 2004[C]. New York: USA, 2004. [11] GWARTNEY J D, STROUP R L, SOBEL R S. Economics: private and public choice[M].王茂斌,吴宏,夏冰,译.北京:机械工业出版社,2000.
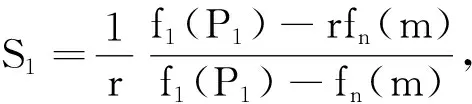



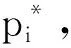
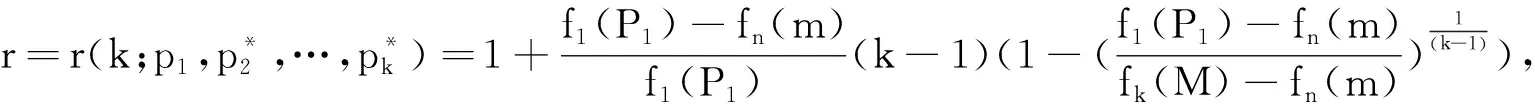


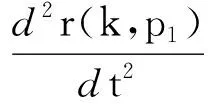


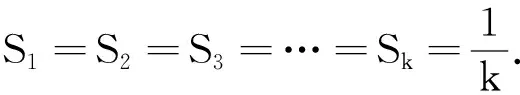

3 实验数值

4 总结

