棉纱线中纤维头端的等效分布研究

严广松，苏玉恒

(1.河南工程学院 数理科学系，河南 郑州 451191；2.河南工程学院 纺织工程系，河南 郑州 450007)

纱线的条干不匀是指纱线沿着纱线长度方向上的线密度不匀，它是纱线质量的重要指标.很多年来，从事纺织基础研究的学者对纱线条干不匀进行了大量的研究，这些研究主要集中在3个方面：一是纱线的极限不匀理论，主要研究纤维的随机排列不匀以及短纤纱所能达到的纱线条干不匀的理论下界问题；二是纱线的长片段不匀，主要研究由纺纱机械造成的附加不匀及其度量问题；三是生产过程中的工艺技术问题，主要研究各个工艺过程技术参数的优化，以生产出均匀的纱线.

纱线不匀的基础理论起源于Martindale[1]，他在1943年给出了纱线极限不匀的理论下界，被后人广泛应用并称为Martindale公式.但是，由于Martindale公式没有包含纤维长度分布对纱线不匀的影响，后来的许多学者都试图改进，以期得到更加客观的纱线极限不匀表达式[2-4].

近年来，由于纺纱技术的发展，纱线的均匀度得到了较大改善.从1997年开始，因为高支纱线的部分不匀率已经超过了纱线均匀度的理论下界，反映世界范围纱线质量指标的USTER公报不再使用由Martindale所定义的不匀率指数[5]，这说明Martindale所给出的纱线极限不匀公式在一定程度上存在着问题.对于纱线理论不匀问题，历史上不少学者都进行了细致的探讨，谋求问题的最终解决.Brown(1985)利用纤维头端在纱线中的分布给出了短纤纱线密度的连续表达[6]，Zeidman等(1998)把纱线均匀度分解为3个部分[7]，Yan(2010)提出了一种纤维在通道中随机排列的模型，得到了纱线截面纤维根数近似服从正态分布的结论[8]，这些研究都为本研究奠定了基础.

按照Martindale所给出的纱线极限不匀公式，纱线的截面面积不匀主要来自于纱线截面纤维根数和纤维细度的变异.而对于棉纱线来讲，纱线截面纤维根数不匀是影响纱线不匀的重要因素.要研究纱线截面纤维根数的变化，一项基础的工作是要研究纤维在纱线中的随机排列.如何使用数学方法来细致地描述这种排列规律是随机排列研究的关键.纤维随机排列的特征可以使用纤维头端在纱线长度方向上的分布来表示.但是，纤维头端在纱线中的位置极难观测到，使用试验的方法得到纤维头端的分布是不现实的.于是，可以假设纤维的头端具有某种分布，而这种分布又取决于一两个分布参数.然后，变动这个分布参数，从而使模拟生成的纱线具有与检测值相等的CV值，称这种与实际分布等效的分布为纤维头端在纱线中的等效分布.这个等效分布显然区分了不同纱线中纤维随机排列的规律，可以用来研究纱线的若干性质.虽然这个分布不是纤维头端的真实分布，但它与真实分布有着同样的效果.

本研究首先定义并讨论了一种满足上述要求的概率分布，称为广义均匀分布.这种广义均匀分布具有一个分布参数，在这个参数等于零时,该分布变成通常的均匀分布.根据一个纱线随机生成的模型，在纱线中纤维长度分布已知且给定纱线的检测不匀条件下，通过变化广义均匀分布参数，模拟出与给定纱线不匀率相等的纱线.这样，所得到的广义分布参数就是纱线中纤维头端的等效分布.

纤维头端等效分布的给出，为定量研究纱线中纤维的随机排列奠定了基础.

1 广义均匀分布

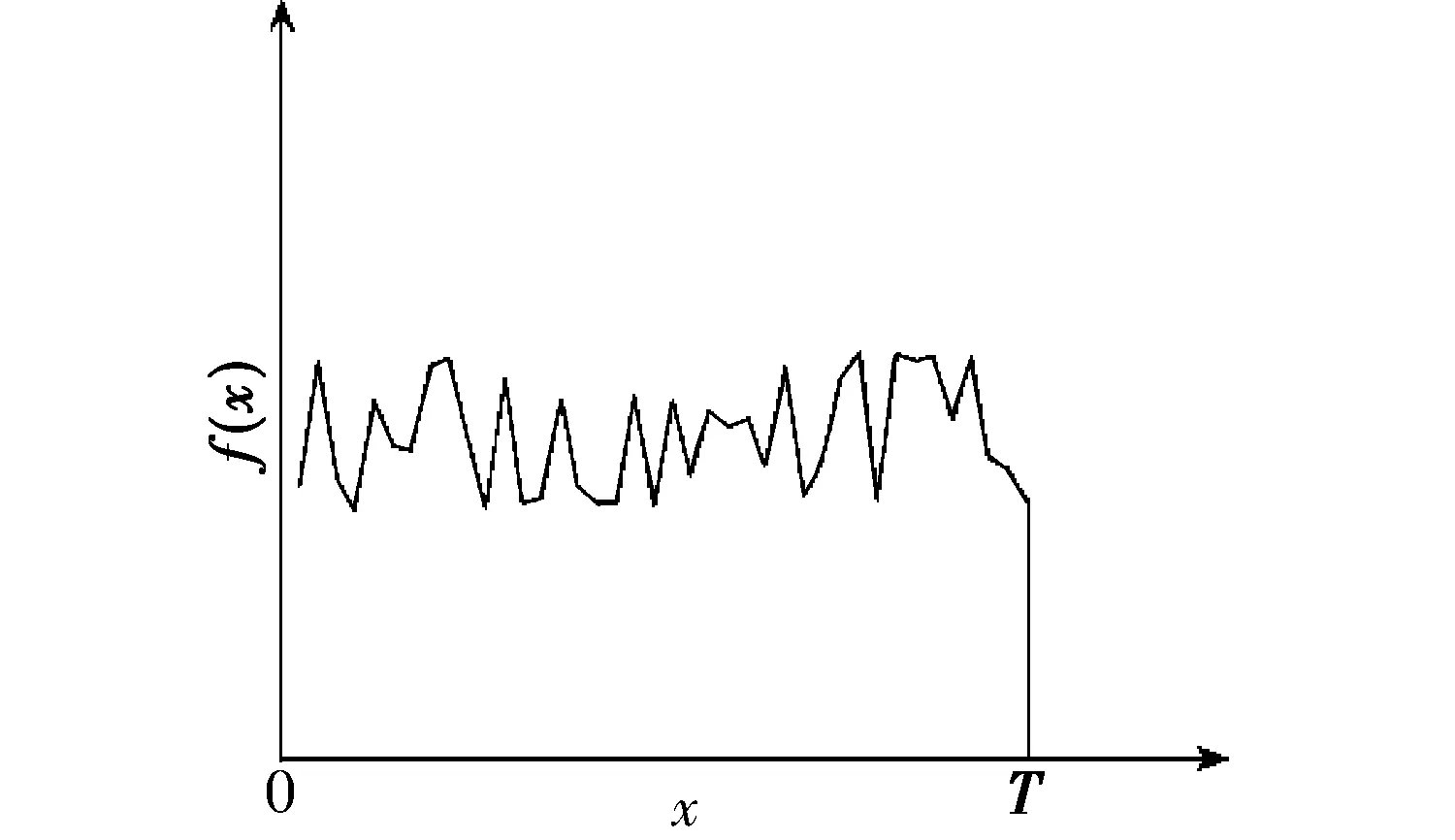
图1 在长度为T的区间上纤维头端分布示意Fig.1 Distribution of fiber ends within [0, T]

假如能够在纱线的一个区段上观测到纤维在纱线中头端的分布，则一定是一个不规则的点的集合，这个点的集合一般不满足均匀分布特征.但是，这种不规则的结构也不会出现极为不平缓的现象，而是呈现总体平稳、局部上有变化的状态，要使用数学方法严格地表示这种分布是比较困难的.实际的纤维头端在纱线长度方向上的分布应该具有图1的形态.

为了描述上述纤维头端的分布状况，定义下列概率密度函数：

这种分布密度的分布参数k表示在小区间上的斜率，当k从0增大时，密度函数的图像会逐渐波动；当k=0时，这个密度函数就变成了通常定义在[0,T]上的普通的均匀分布，称这种密度函数为区间[0,T]上的具有参数k的广义均匀分布.

广义均匀分布还取决于参数n.实际上，广义均匀分布可以看成是从普通的均匀分布生成的，也就是将普通的均匀分布在其定义区间上等分为2n部分，然后将区间上每一等分部分的函数直线按照统一的斜率k转动一个角度，就生成了广义均匀分布.通常，n是一个事先确定的数，而参数k是一个变数.

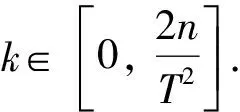
广义均匀分布具有期望和方差.

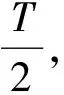
广义均匀分布密度函数的图像见图2，分布函数的图像见图3.

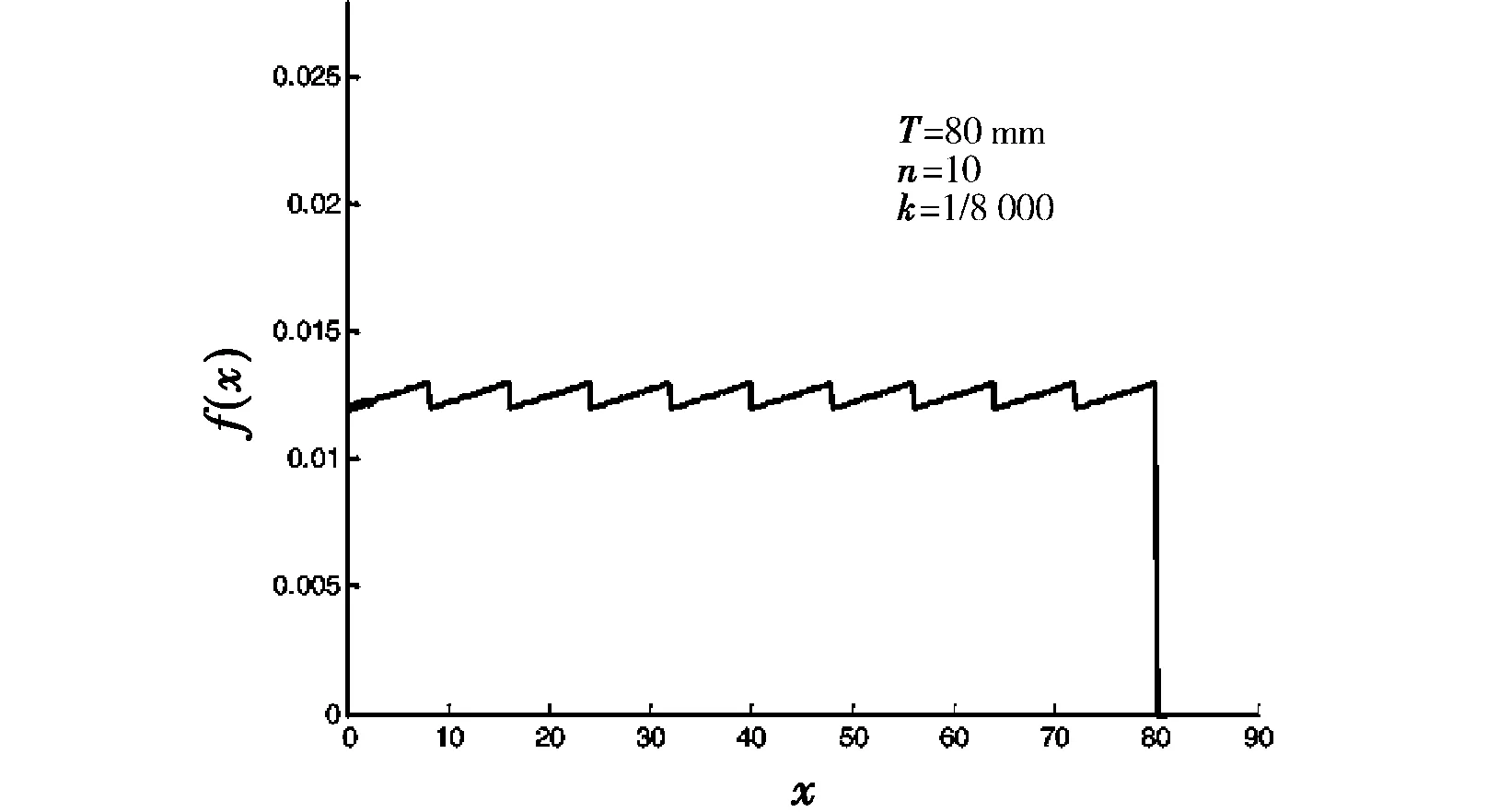
图2 广义均匀分布密度函数Fig.2 Density function of generalized uniform distribution

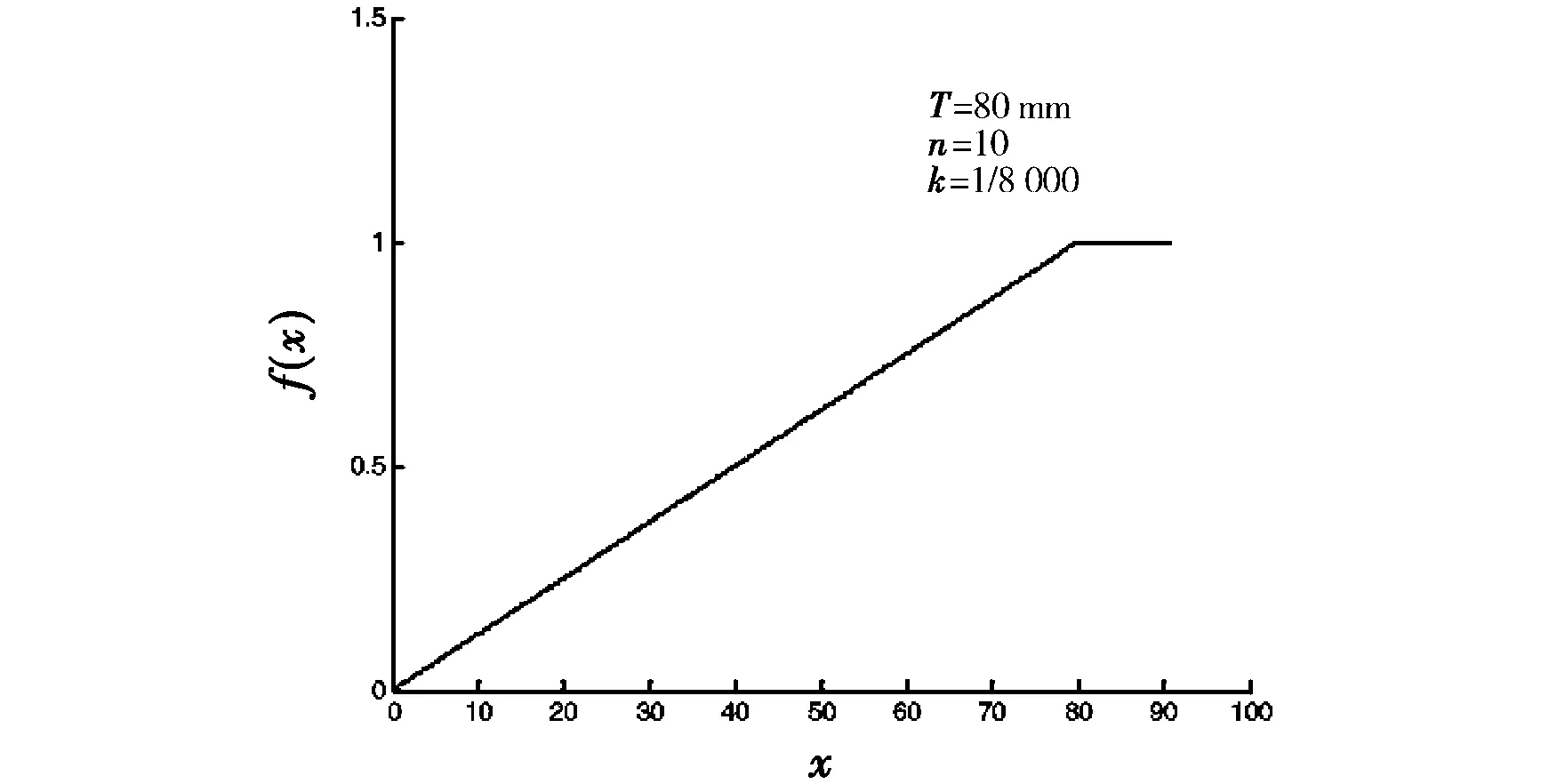
图3 广义均匀分布的分布函数Fig.3 Distribution function of generalized uniform distribution

2 纱线不匀的模拟模型

纱线的均匀度可以通过随机模拟的方法得到.需要指出的是，纱线的均匀度在实际中都是采用检测的纱线不匀率来表示.按照电容式纱线条干仪的原理，检测的不匀率是使用8 mm电容板上纤维量的变异来表示的，所以在对纱线不匀率进行模拟时，可以采用计算机程序来计算8 mm上纤维量的变异.

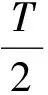
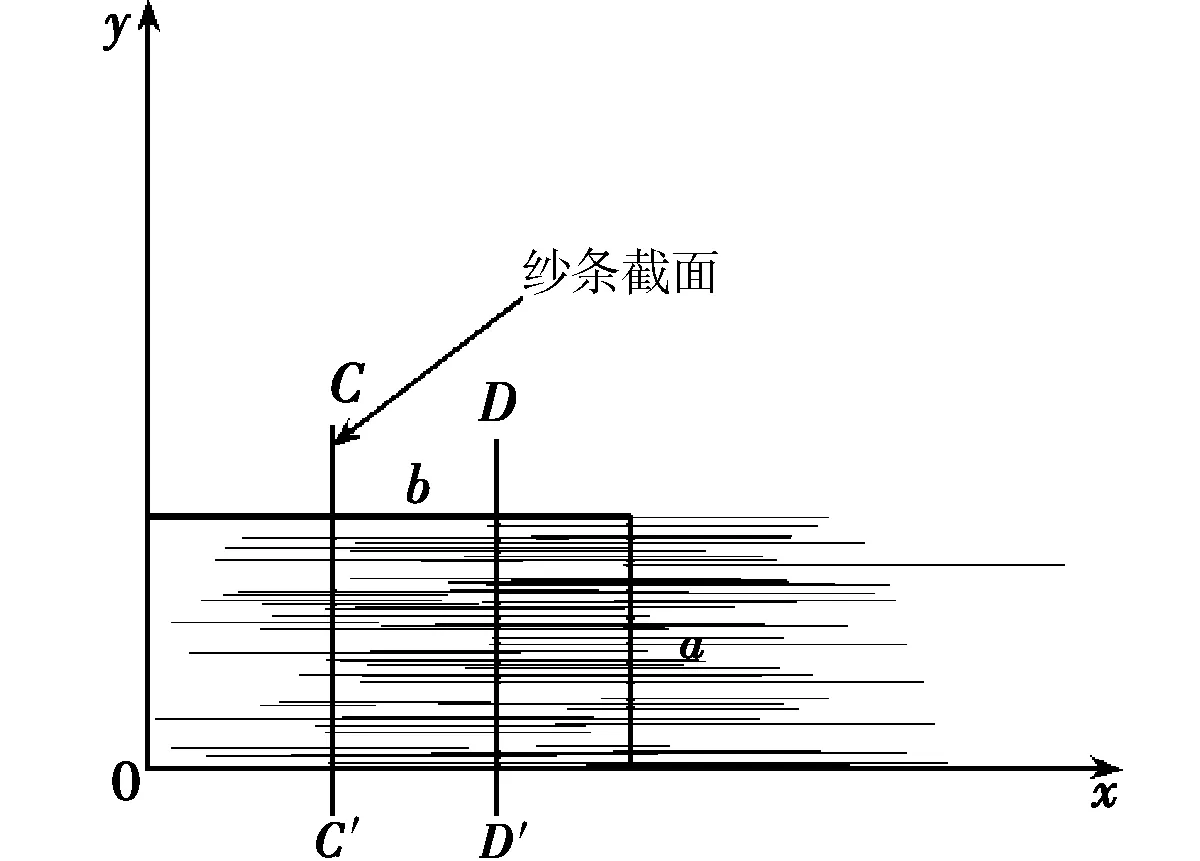
图4 纱线模拟方法Fig.4 Simulation of the yarn

在区间[0,a]中按照广义均匀分布持续生成纤维的左头端点及其纤维长度，就可以通过程序来计算平面C-C′和平面D-D′之间的纤维量，而这个纤维量就是纱线条干仪在8 mm上检测的模拟值.反复进行这样的生成和计数，就可以得到8 mm上纤维量的CV值.

对于一个给定的纱线，如果已经测出纱线中纤维的长度根数分布，又测出纱线的不匀率，那么，就可以按照上述的模拟方法，不断改变广义均匀分布的分布参数k，直到平面C-C′和平面D-D′之间的纤维量的CV值与检测的纱线CV值相当，便得到了广义均匀分布参数k0.

在实际模拟过程中，还需要根据纱线截面的纤维根数来确定纤维头端点的生成个数.在给定纱线截面的平均根数以后，通过对平面C-C′上的观测程序，可以得到模拟次数和截面平均纤维根数的关系.纱线模拟模型具有一定的随机性，符合纱线中纤维排列的一般规律.

3 纤维头端等效分布的计算

按照上述纱线模拟模型及其方法，在给定纱线支数和纤维长度分布以后，就可以计算出纱线中纤维头端的等效分布.选定2种纱线，其组成纤维的长度分布如图5所示.2种纱线的实测和模拟值见表1.

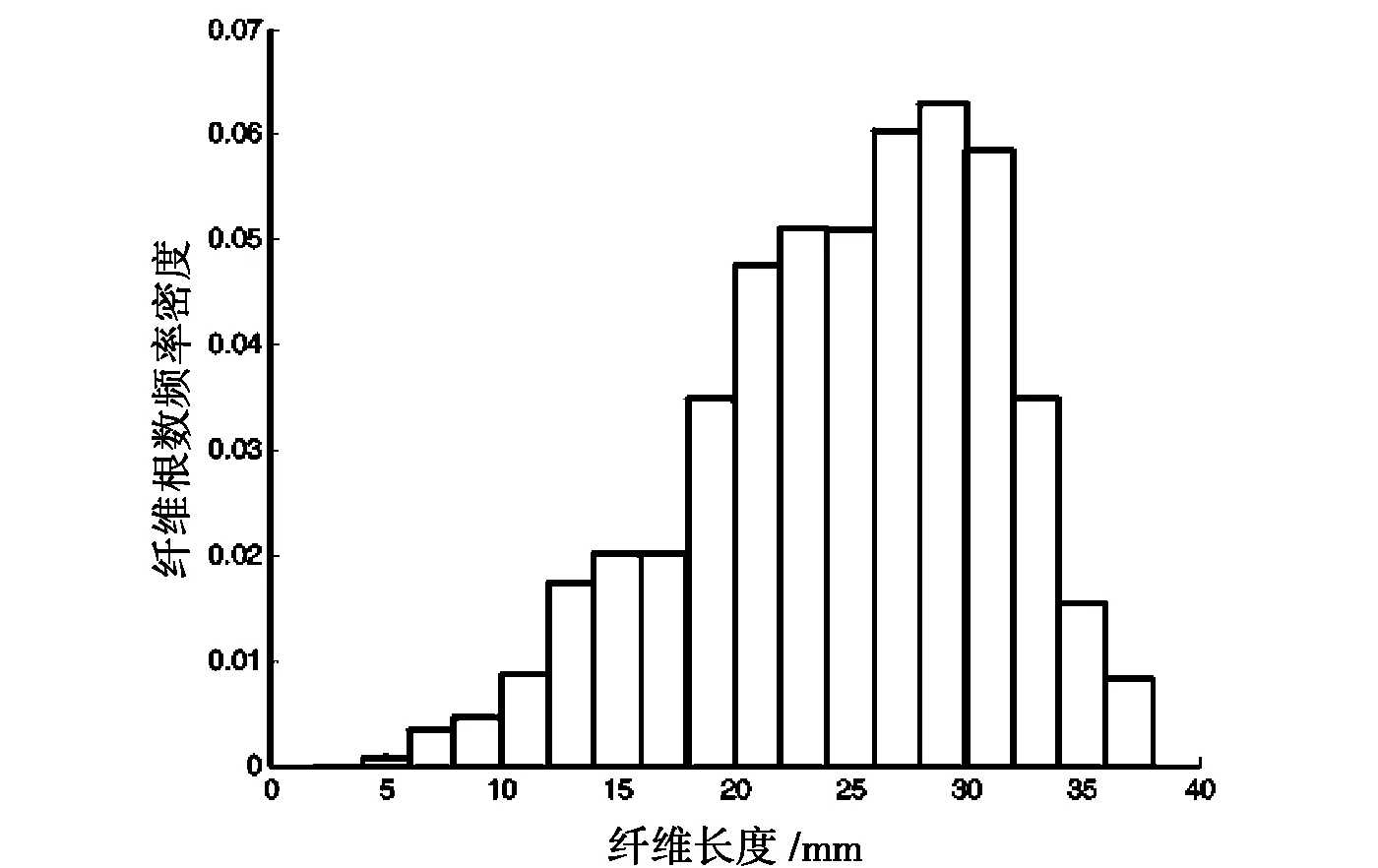
图5 纤维长度分布直方图Fig.5 Rectangle of fiber length distribution

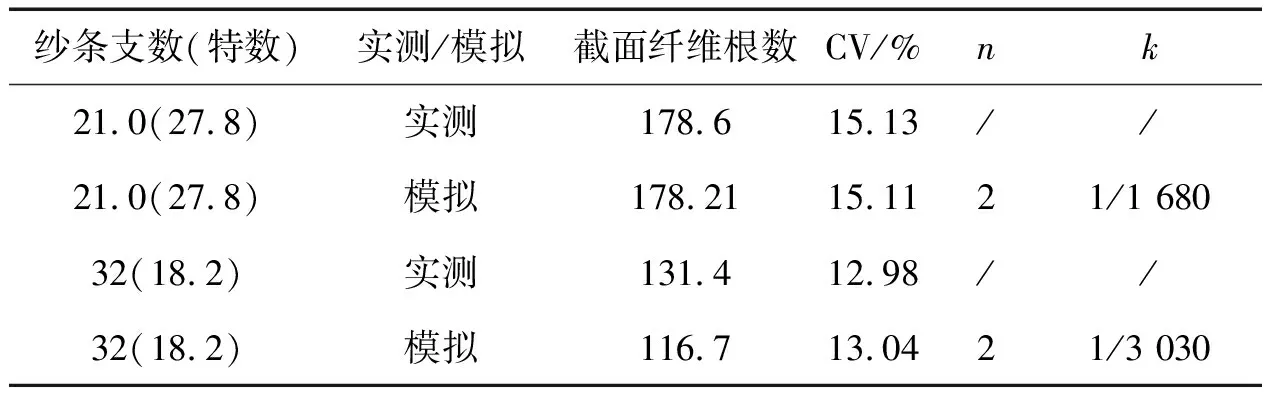
表1 模拟与实测不匀表Tab.1 Simulated and tested unevenness

表1的模拟结果表明，给定的纱线具有不同的CV值，而通过反演得到的广义均匀分布参数极小，分别是1/1 680和1/3 030，纤维头端的分布接近普通的均匀分布.而且，k值越小，相应模拟得到的纱线CV值也越小，这说明普通的均匀分布是纱线达到最小CV值时的纤维头端分布.在纺纱时，无论纤维长度的分布如何，都应该使纤维头端在纱线长度方向上呈均匀分布，才能使纱线的均匀度提高.

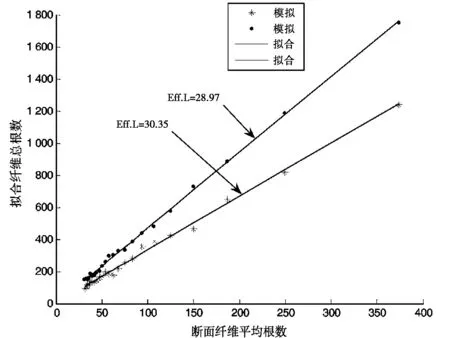
图6 2种纤维长度分布断面纤维平均根数与总根数关系Fig.6 Average simulated number of fibers and the number of fibers in yarn cross section for two length distributions

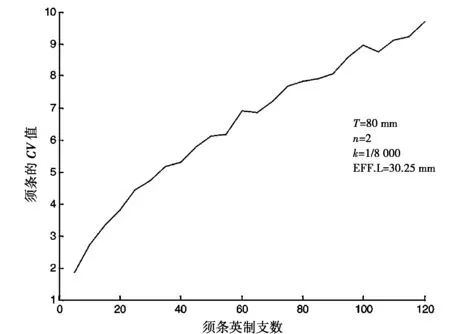
图7 纱线支数与模拟的CV值Fig.7 Simulated yarn CV versus yarn counts

图6是在2种不同的纤维长度分布下，80 mm纱条片段内纤维断面平均根数与总根数关系的模拟结果及其最小二乘线性拟合直线.模拟表明，在一定的纱条片段长度上，纱条有效截面(即不包括纱条尾部无纤维右头端延伸部分)内平均纤维根数与片段内纤维的总根数为明显线性关系，纤维长度不同时，其斜率不同，这说明了不同的纤维长度分布对生成纱线均匀度的影响.

图7是在纤维头端为广义均匀分布下对纱线不匀率的模拟，纤维的有效长度选择为30.25 mm.模拟表明，随着纱线英制支数的增大，也就是纱线变细时，纱线的不匀率会随之上升.这显然是符合实测结论的，也从另一个侧面说明了广义均匀分布具有较好的拟合纤维头端实际分布的特性.

4 结论

根据纤维头端分布的特征，对于纱线中纤维头端分布的不可观测性，定义了一种新的、可变动的广义均匀分布.按照纱线随机生成的原理，使用反演的方法，在已知纱线中纤维长度分布和纱线不匀率的条件下，得到了纤维头端的广义均匀分布参数估计.模拟表明，当纤维头端分布接近普通均匀分布时，纱线的均匀度提高；反之，纱线的均匀度下降.结果还表明，使用广义均匀分布作为纤维头端分布还可以模拟生成一定范围均匀度的纱线，对于研究纱线不匀的原因和结构具有一定意义.

但是，纤维头端在纱线中的分布具有相当的复杂性和随机性，对于纱线检测中的粗节和细节等问题，如何使用上述方法进行分析，尚需要进一步的研究.

参考文献：

[1] Martindale J G. A new method of measuring the irregularity of yarns with some observations on the origin of irregularity in worsted slivers and yarns[J]. J Text Inst, 1943(36): 35-47.

[2] Suh M W. Probabilistic assessment of irregularity in random fiber arrays-effect of fiber length distribution on "variance-length curve"[J]. Textile Research Journal, 1976(45): 291-298.

[3] Zeidman M I. A new perspective on yarn unevenness: components and determinants of general unevenness[J]. Textile Research Journal, 1990, 49(1): 28-34.

[4] Dyson E. Some observations on yarn irregularity[J]. J Text Inst, 1974, 65(2): 215-217.

[5] 李友仁. 电容式条干仪在纱线质量控制中的应用[M]. 北京：中国纺织出版社，2006: 28-38.

[6] Brown G H, Ly G N. Statistics for the number of fiber ends in a segment of a random assembly of aligned fibers[J]. Textile Research Journal, 1985, 55(4): 206-210.

[7] Zeidman M, Suh M W, Batra S K. A new perspective on yarn unevenness: components and determinants of general unevenness [J]. Textile Research Journal, 1998, 56(4): 1-6.

[8] Yan Guangsong, Zhu Jinzhong, Yu Chongwen. A new approach to theoretical yarn unevenness: a binomial distribution model[J]. J Text Inst，2010,101(8): 753-757.