基于多层感知器神经元的空间柔性机器人位置跟踪控制*

张文辉，马 静，高九州

(1.哈尔滨工业大学航天学院，哈尔滨150001；2.东北农业大学工程学院，哈尔滨150001)

基于多层感知器神经元的空间柔性机器人位置跟踪控制*

张文辉1，马 静2，高九州1

(1.哈尔滨工业大学航天学院，哈尔滨150001；2.东北农业大学工程学院，哈尔滨150001)

针对基体位置及姿态均不受控的自由漂浮柔性空间机器人轨迹跟踪问题，提出了一种前馈多层感知器(MLP)神经网络控制策略.建立了末端柔性的自由漂浮基机器人的耦合动力学模型，再利用MLP神经网络良好的逼近能力来自适应补偿非线性柔性臂的逆动力学模型，其误差代价函数由PID控制器提供，权重及阀值的调整采用改进的BP反传算法.最后通过仿真比较详细分析了所提方案的工作机理及对非线性强耦合系统控制的有效性.

多层感知器神经网络；逆模控制；PID控制；BP算法

柔性臂由于质量轻、速度快等一系列优点逐渐引起了学术界的广泛兴趣.但空间柔性机器人系统为非完整动力学系统，存在着强烈的动力学耦合作用［1-3］，从而导致空间柔性机器人在运动过程中出现振动，在运动结束时产生残余振动，影响控制性能.由于传统的动力学控制方法已不能满足空间柔性机器人动力学控制的要求，为消除这些非线性因素的影响，目前自适应控制、模糊控制等先进的控制策略［4-7］已应用到柔性空间机器人跟踪控制中.

由于模糊控制无需知道被控制对象的精确数学模型，且控制器结构简单，并具有学习能力，因而在空间控制领域的应用日益广泛，已取得了一定成果.文献［4-5］提出了的一种模糊控制方案用于空间柔性臂，模糊规则通过自适应律来调整，达到了较好的控制效果，但由于模糊规则的获取需要先验的专家知识，且过多的模糊规则将造成较大的将计算量，因而很难应用于工程实际.文献［6］考虑到柔性空间机器人在自由漂浮模式下动力学模型难以准确得到，并且容易受到非线性不确定性的影响，因而采用自适应控制策略，获得了较好的控制效果，但自适应控制律的获得需要参数线性化及回归矩阵的确定，因此需要大量计算，影响了实时性.

本文针对基体的位置及姿态均不受控的漂浮柔性空间机器人，提出了一种改进BP算法的前馈多层感知器神经网络逆模控制策略.利用 MLPNN良好的逼近能力来自适应补偿非线性柔性臂的逆动力学模型.仿真结果详细分析了所提方案的工作机理及对非线性强耦合系统控制的有效性.

1 柔性空间机器人动力学建模

由刚性杆B1及柔性杆B2组成的柔性漂浮空间机器人系统结构如图1所示.设 O1在O0x0轴上与O0的距离为l0，OB1沿 O1x1的长度为 a，Bi沿 Oixi的长度为li(i=1，2)，载体质量为m0，惯量矩阵为I0，B1为刚性杆，质量为m1，惯量矩阵为 I1.

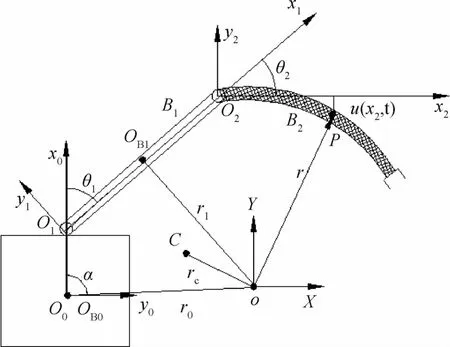
图1 柔性臂漂浮基空间机器人

B2为柔性杆，必然会在运动过程中产生形变，将其视为一段 Euler-Bernoulli梁处理，设其密度为ρ，柔性梁的弹性位移u的模态函数展开表示为

式中，φi(x2)为柔性杆第i阶模态函数，qi(t)为与φi(x2)对应的模态坐标，n为截断项数.

由于不考虑重力的作用，整个系统重力势能为零，且柔性机器人为线弹性变形，故系统总势能 U等于柔性连杆的弯曲应变能.系统遵守对(OXY)的动量守恒及相对O点的动量矩守恒.设系统的初始动量、动量矩均为0，即有˙rc=rc=0.

由材料力学相关理论，系统弹性势能为

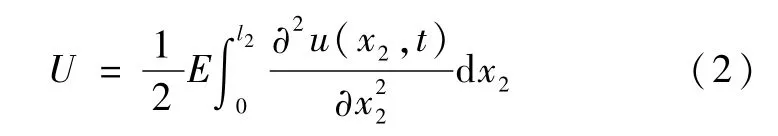
式中，E为抗弯刚度，设α、θ1及θ2分别为载体姿态及机器人各个关节的相对转角，在以α、θ1、θ2、q1及q2为广义坐标的情况下，设系统的总动能为T，则系统的拉氏函数为

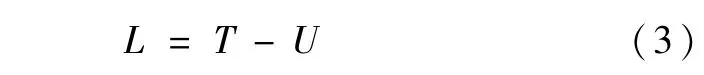
应用拉格朗日方程可得

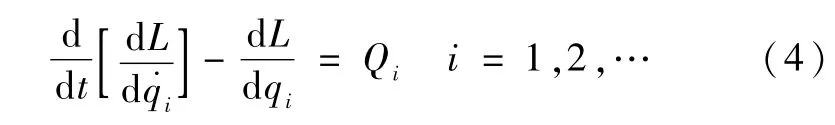
其中，L是系统的拉格朗日函数，qi为系统的广义坐标，Qi为广义坐标qi相对应的广义力.

结合式(3)～(4)，经过推导和整理，可以得到如下空间刚柔机器人系统的非线性动力学方程：

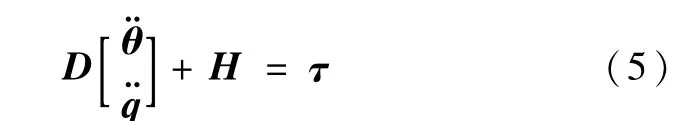
其中 θ=［θ1θ2］T，q=［q1q2］T.D为 4 ×4 正定对称广义质量阵.H为4×1哥氏力、离心力和弹性力的列阵.τ=［τ1τ20 0］T为控制力矩.

2 多层感知器神经元控制器设计

文中定义 φ=［θTqT］T为增广输入向量，φd=［qT］T为增广的期望关节角，采用扩展系统的增广变量输入法.则可以得出系统误差向量e=φd-φ=［0］，这里 eθ=θd-θ.

在式(5)不存在未建模动态及外界扰动的情况下，下面的控制器(6)可以保证系统的稳定性.

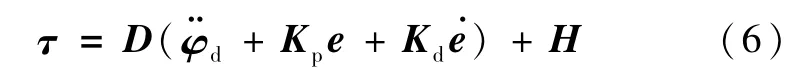
这里定义Kp、Kd为反馈增益矩阵.

在实际中，空间柔性机器人的模型很难精确得到，只能建立估计模型.设估计模型为.对于估计模型，则控制律设计为

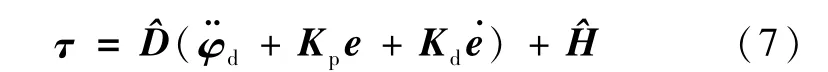
这里将控制律式(7)代入控制律式(6)中，得

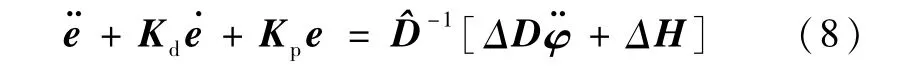
为解决空间柔性机器人非线性动力学模型的误差影响，这里考虑采用多层感知器神经网络(MLPNN)来对柔性空间机器人的逆动力学模型进行逼近.

前馈多层感知器神经网络是大量具有神经元级的联层网络，同一层的所有神经元通过单向分支连接邻近层的所有神经元，分支或连接仅能向一个方向，即“前馈方向”传递信息，已经证明只要有足够的神经元，它就能以任意精度逼近非线性函数.

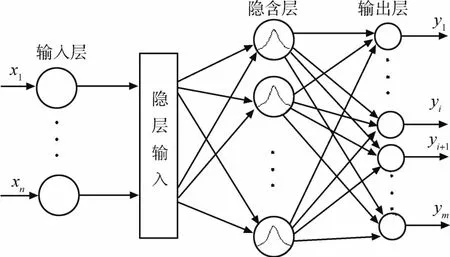
图2 多层感知器神经网络

由柔性空间机器人非线性动力学模型(5)得

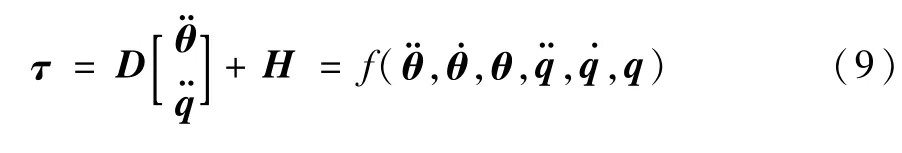
柔性空间机器人的MLP网络逆模控制系统如图3所示，这里控制输入τ由PID反馈控制器τPD和MLP神经网络逆模学习控制器τNN组成.

设计PID反馈控制器为

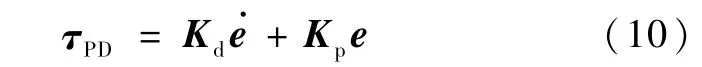
MLP神经网络控制器设计为

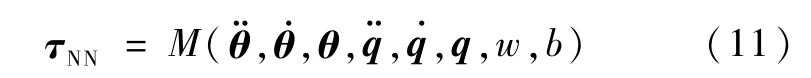
其中，w为神经网络连接权值，b为神经网络节点阀值.则

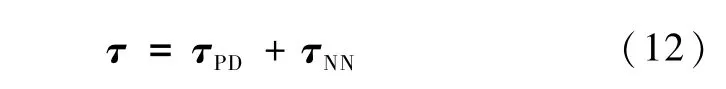
控制系统结构如图3所示.

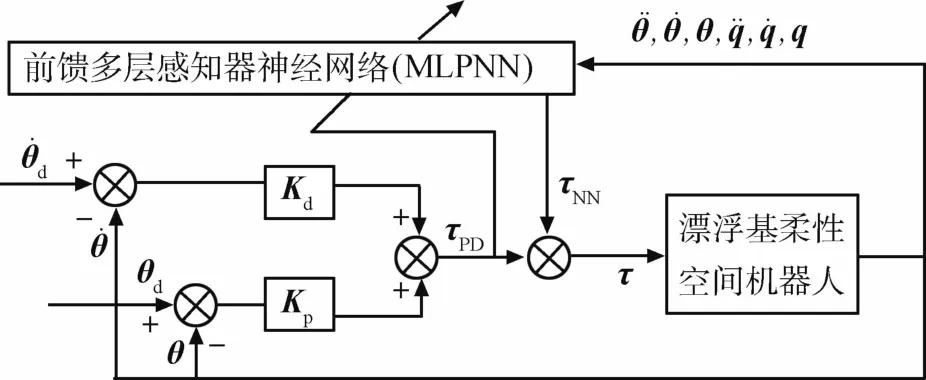
图3 神经网络逆模控制系统

由图3中可以看出随着τNN对逆动力学模型学习的进行，τPD越来越小.

由此可以定义MLP神经网络的学习误差δ为

为保证实时性，便于工程应用，本文采用一种改进的BP算法来完成包括网络参数的更新训练，使学习误差趋于0为实际网络输出向量，yd为网络期望输出向量.

这里设前向神经网络有M层，每层输入输出关系为

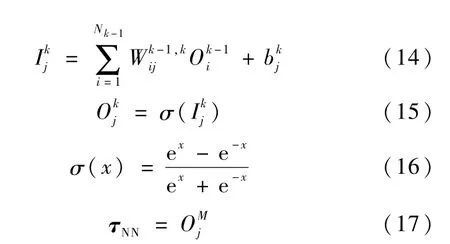
采用反向传播算法，则前向网络连接权值及阀值的修正公式为

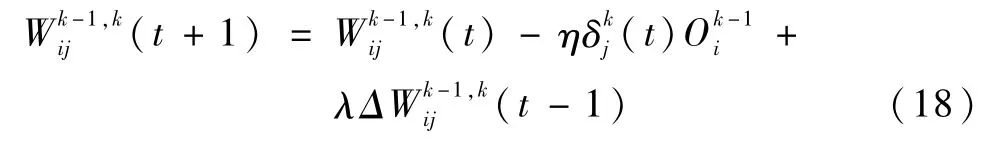
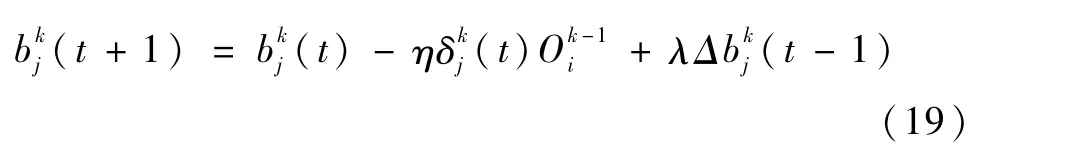
通过上述前馈多层感知器神经元的参数更新算法，在线边学习边控制，MLPNN将逐渐建立比较精确的空间柔性机器人的系统逆模型.

3 仿真算例及分析

空间柔性机器人系统的惯性参数为l0=0.6m，l1=l2=1.2m，a=1m；各分体质量或密度 m0=50kg，m1=5kg，ρ=0.6kg/m；均匀弯曲刚度为 E=360N·m2.各分体中心惯量矩 I0=35kg·m2，I1=0.8kg·m2.从泰勒的角度来看，忽略高阶模态，仅取前两项，柔性空间机器人两关节期望的轨迹为

θ1d=1+0.2cos(πt) ；θ2d=1+0.2sin(πt)；控制器增益 Kp=diag{20，20} ，Kd=diag{30，30}；神经网络参数为λ=0.25，η=0.7；初始值分别取为 θ1(0)=θ2(0)=1.

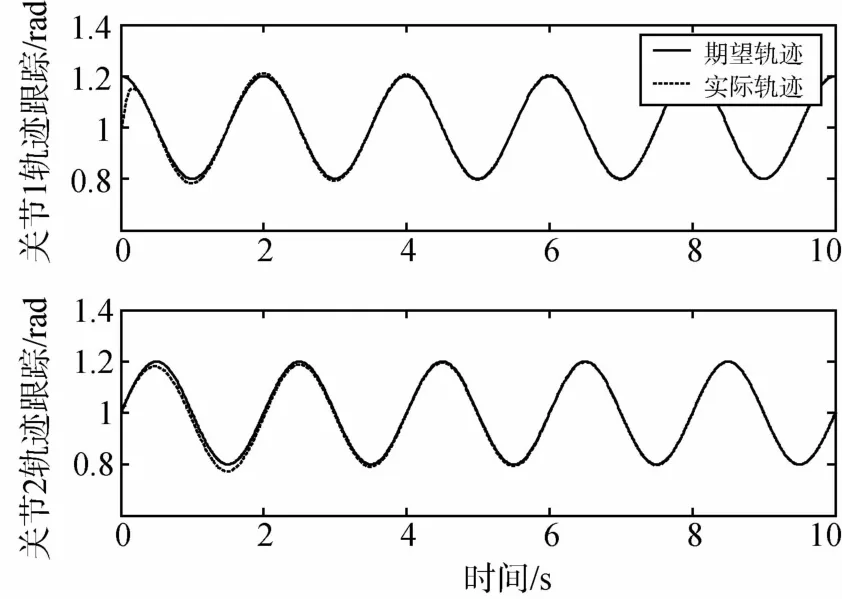
图4 本文的轨迹跟踪情形图

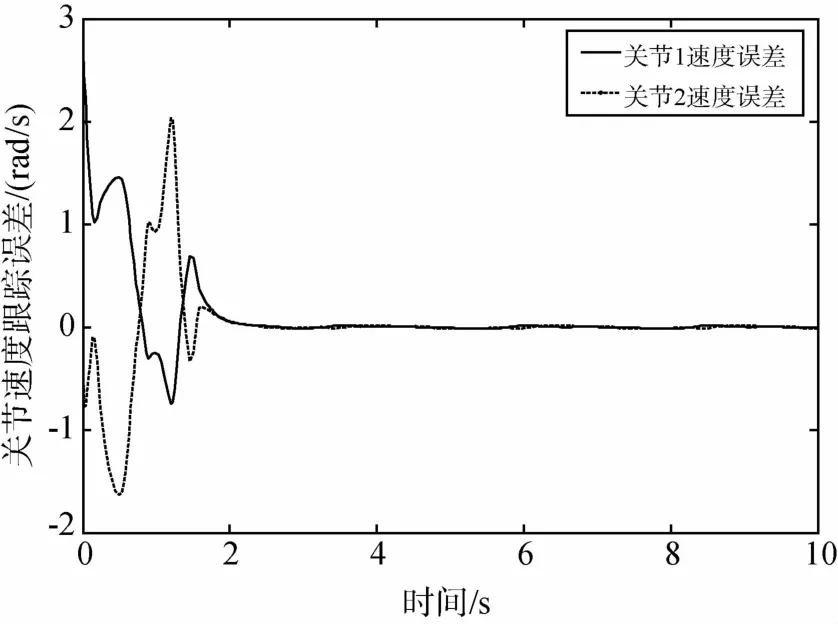
图5 本文的关节速度跟踪误差图

而由图4可以看出，所设计的MLP神经网络的逆模PID控制器能在较短时间(t=2s)内快速跟踪期望轨迹，同时由图5看出，角速度跟踪误差在2s后也收敛为0，说明多层感知器神经元能够较好控制非线性强耦合的空间柔性机器人系统.

4 结 论

针对自由漂浮的柔性空间机器人系统的关节位置跟踪问题，提出了一种改进BP算法的前馈多层感知器神经网络逆模控制策略.利用多层感知前馈神经网络良好的逼近能力来自适应补偿非线性柔性臂的逆动力学模型，神经网络的误差代价函数由传统的PID控制器提供，权值及阀值的调整采用改进的BP反传算法.仿真说明了所提方案的有效性，对于非线性强耦合系统能够获得较高控制精度.

［1］Farzaneh A，Talebi H A，Rajnikant V P.A stable neural network-based observer with application to flexiblejointmanipulators［J］.IEEE Trans on Neural Networks，2006，17(1)：118-129

［2］Dubowsky S ，Papadopoulos E G.The kinematics， dynamics and control of free-flying space robotic systems［J］.IEEE Trans on Robotics and Automation， 1993，9(5)：531-543

［3］Amor J，William A.Experimental study on active vibration control of a single-Link flexible manipulator using tools of fuzzy logic and neural networks［J］.IEEE Trans on Instrumentation and Measurement， 2005， 54(3)：1200-1208

［4］Green A，Sasiadek JZ.Adaptive control of a flexible robot using fuzzy logic［C］.AIAA Guidance， Navigation，and Control Conference and Exhibit， Providence， Aug.16-19，2004

［5］张晓东，贾庆轩，孙汉旭，等.空间机器人柔性关节轨迹控制研究［J］.宇航学报，2008，29(6)：1865-1869

［6］Chen L.Adaptive and robust composite control of coordinated motion of space robot system with prismatic joint［C］.The 4thWorld Congress on Intelligent Control and Automation， Shanghai，2002

Position Tracking Control for Space Flexib le Robot Based on M u ltilayer Percep tual Neural Network

ZHANG Wenhui1，MA Jing2， GAO Jiuzhou1
(1.School of Aerospace，Harbin Institute of Technology，Harbin 150001，China； 2.Department of Engineering，Northeast Agriculture University， Harbin 150001，China)

The problem of trajectory tracking for freefloating space robotwith flexible manipulators are considered.An improved multilayer perceptual neural network(MLPNN)inverse-model control algorithm based on the BP algorithm is proposed in this paper.High order liberation modal is ignored based on the assumed modalmethod，Lagrange principle and momentum con-

servation.The MLPNN based controller is used to adaptively learn and compensate the inverse-dynamics model of robot，neural network parameters can be adaptively adjusted on line，and the improved BP algorithm is adopted to learn rules.Error cost function is provided by PID controller.The controller improves the control accuracy and the asymptotic convergence of tracking error.The simulation results show that the presented controller has important value.

multilayer perceptual neural network； inverse-modal control； PID control； BP algorithm

TP242

A

1674-1579(2011)01-0059-04

10.3969/j.issn.1674-1579.2011.01.013

*中国航天科技联合创新基金(CAST-HIT09C01)资助项目.

2010-09-15

张文辉(1980—)，男，河南人，博士研究生，研究方向为空间机器人智能控制 (e-mail：hit-zwh@126.com).