感知器在矿井突水水源识别中的应用
彭 程,刘永涛,尤文强,马红梅
(1.华北科技学院电子信息工程学院,河北 三河 065201;2.应急管理部煤炭安全监测监控技术安全生产重点实验室,河北 三河 065201)
矿井突水是煤矿生产安全的主要威胁之一,一旦发生突水事故,快速准确判断水源对及时处置事故、减小损失有重要意义。利用矿井突水的化学成分识别水源是其中一类重要方法。针对突水化学数据,学者们采用了数量化理论[1]、聚类分析[2]、多组逐步Bayes判别[3]、熵权模糊综合评价[4]、动态自适应模板[5]、可拓识别[6]等方法,建立了突水水源识别模型。
神经网络因其具有学习能力也被用于矿井突水水源识别,当前应用较多的神经网络模型有:BP神经网络[7]、Elman神经网络[8]和RBF神经网络[9]等。上述文献使用神经网络分类器均取得了较好的识别效果,但是也存在两个缺点:一是神经网络训练算法较为复杂且收敛性缺乏理论保证,训练时有可能陷入局部极小点;二是在构造神经网络进行突水水源识别时,使用了多种类型的水化学数据,造成网络结构复杂,也增大了水化学数据测量的工作量。感知器是一种线性神经网络分类器,具有训练简单可靠的优点。能否构造尽可能简单的感知器模型识别矿井突水水源,是本文研究的问题。
1 感知器模型及其训练方法
感知器结构见图1,其输入输出关系可以表示为式(1)。
y=f(wx-θ)
(1)
式中:x=[x1,x2,…,xm]T∈Rm、y=[y1,y2,…,yn]T∈Rn分别为感知器的输入向量和输出向量;w=[w1,w2,…,wm]∈Rn×m为权值矩阵;w的第k(k=1,2,…,m)列wk=[w1k,w2k,…,wnk]T∈Rn;θ=[θ1,θ2,…,θn]T∈Rn为阈值向量;激活函数f(·)定义为式(2)。
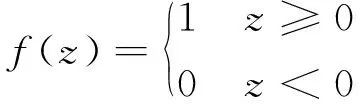
(2)
式中,z∈R。

图1 感知器结构图Fig.1 Architecture of perceptron
式(1)中激活函数f(·)的运算应理解成对列向量wx-θ的每个分量分别按式(2)进行计算。如果在感知器模型中将与阈值向量θ对应的“-1”作为输入向量的一部分,则感知器模型也可以表示为式(3)。

(3)
式中,W=[wθ]∈Rn×(m+1)为增广后的权值矩阵。由式(3)和图1可知,感知器模型不含有隐含层,结构上比BP、RBF、Elman等多层神经网络简单。
感知器的训练(也称为学习)即为利用若干组训练用输入向量x1、x2、…、xD及其对应的期望输出向量t1,t2、…、tD确定权值矩阵W的过程,可以按照式(4)定义的方式依次利用每一组输入、输出向量更新权值矩阵,见式(4)。
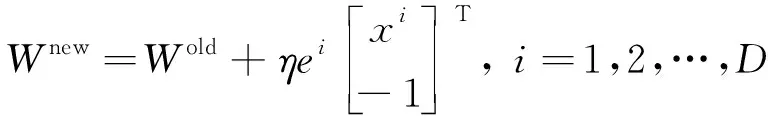
(4)
式中:Wold和Wnew分别为更新前后的权值矩阵;η>0为学习率;感知器输出误差向量见式(5)。
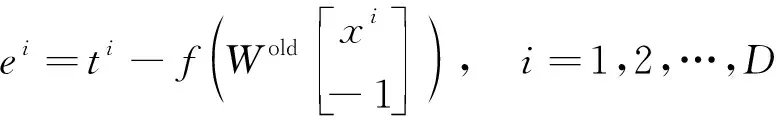
(5)
每组训练用输入、输出向量均使用过一次之后,称为训练完成了一代,此时得到的感知器通常无法达到使用的要求,训练需要重复若干代。在训练过程的第g代,利用在权值矩阵更新过程中求得的误差向量ei,计算第g代的总误差见式(6)。

(6)
若Eg=0,说明在训练过程的第g代,权值矩阵W没有更新,并且对于所有训练用输入向量而言,感知器输出向量与期望输出向量均一致,即此时感知器正确地对训练样本进行了分类。故对于可以用感知器进行分类的问题,可以用Eg=0作为训练结束的判断条件。
对于不能用感知器分类的问题,总误差Eg永远不会等于0,为了防止此种情况导致的训练不收敛,感知器学习算法中需要设置一个参数:最大训练代数G,作为训练结束的条件,G应取一充分大的自然数。
本文实现的感知器在训练开始之前进行了归一化处理,设原始的输入向量为u1、u2、…、uD,则训练用输入可以由
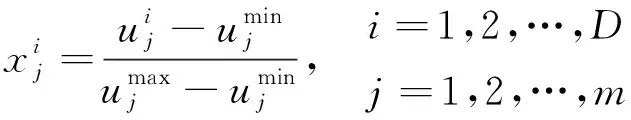
(7)
得到,其中
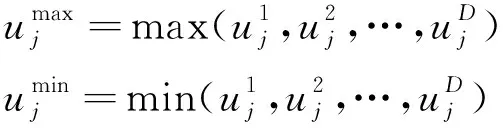
(8)
容易知道,归一化操作后训练用输入向量x1、x2、…、xD的各分量均位于区间[0,1]之内。
综上所述,使用感知器进行突水水源识别的算法流程如下所述。
步骤1:按照式(7)对原始输入向量u1、u2、…、uD进行归一化处理,得到训练用输入向量x1、x2、…、xD;确定x1、x2、…、xD各自对应的期望输出向量t1、t2、…、tD;由输入向量和期望输出向量的维数确定感知器权值矩阵W的维数。
步骤2:设置训练参数,包括学习率η和最大训练代数G。
步骤3:随机生成初始权值矩阵W;由式(5)计算初始权值下各输入向量对应的输出误差向量,由式(6)计算初始权值下的总误差E0;令当前训练代数g=0。
步骤4:若Eg=0,训练成功,结束训练过程,转到步骤8。
步骤5:令g=g+1;若g>G,训练失败,退出程序;否则,令训练数据组数i=1。
步骤6:以xi为输入向量、ti为期望输出向量,按照式(5)计算输出误差向量ei,按照式(4)更新权值矩阵W。
步骤7:令i=i+1;若i>D,由式(6)计算第g代的总误差Eg,返回步骤4;否则返回步骤6。
2 矿井突水水源的感知器识别

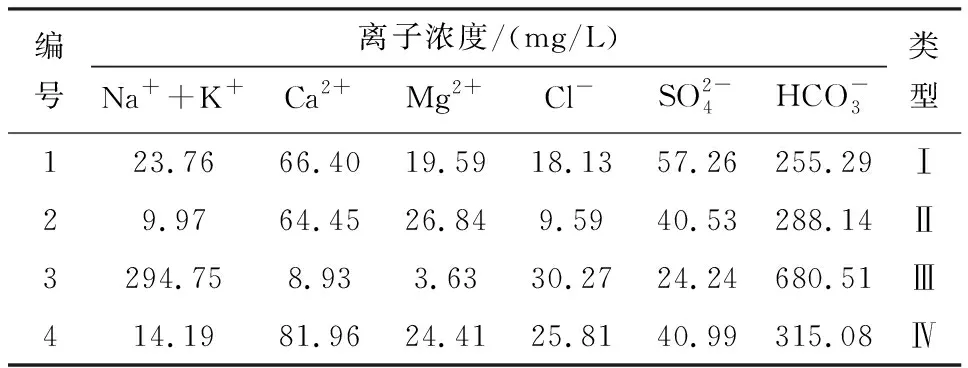
表1 测试样本Table 1 Testing samples
为了能够简化感知器模型的结构,在不损失训练和识别精度的情况下,应尽可能减少感知器输入的维数。能够获取的离子浓度信息共有六种,若使用其中的m(1≤m≤6)种离子的浓度作为感知器输入,则可以构造一个具有(m+1)个输入的感知器进行水源识别,前m个输入分别对应于一种离子的浓度(需按照式(7)进行归一化处理),最后1个输入为与阈值向量θ对应的-1。容易知道,感知器模型的输入组合共有26-1=63种,本文采用枚举法对这63种情况下的感知器逐一进行训练。水样共有4类,将其表示为四个列向量:[1 0 0 0]T(类型Ⅰ)、[0 1 0 0]T(类型Ⅱ)、[0 0 1 0]T(类型Ⅲ)和[0 0 0 1]T(类型Ⅳ),作为感知器的期望输出向量。

式(6)定义的总误差Eg随训练代数g的变化过程见图2。由图2可知,感知器训练过程中,总误差Eg并不总是随着训练代数g逐渐下降,而是具有波动性,但是经过一定代数的训练之后总误差Eg能够收敛到0。
利用式(7)的方式处理表1中4组测试数据,将结果输入训练得到的感知器,得到的识别结果见表2,可知感知器正确识别了测试水样的类型。根据感知器训练和识别的结果可以知道焦作矿区突水水源识别问题是线性可分的。
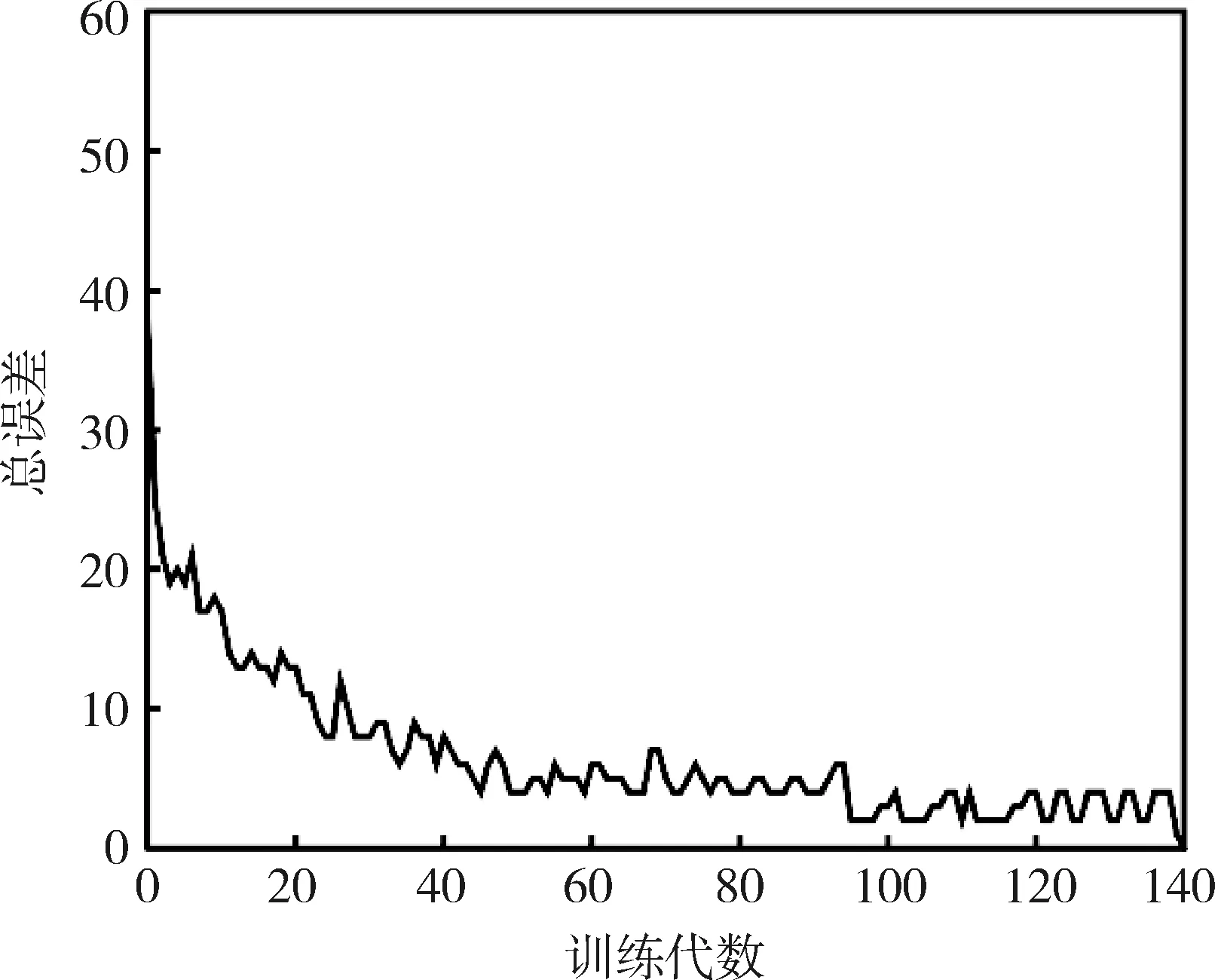
图2 感知器总误差收敛曲线Fig.2 Convergence curve of total error of perceptron
表2 感知器识别结果Table 2 Recognition results of perceptron
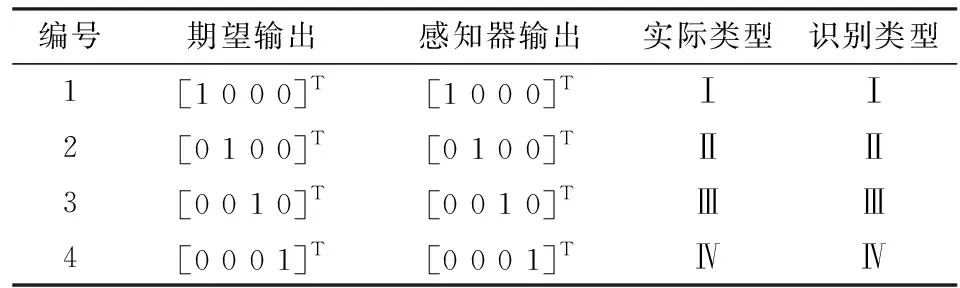
编号期望输出感知器输出实际类型识别类型1[1 0 0 0]T[1 0 0 0]TⅠⅠ2[0 1 0 0]T[0 1 0 0]TⅡⅡ3[0 0 1 0]T[0 0 1 0]TⅢⅢ4[0 0 0 1]T[0 0 0 1]TⅣⅣ
由于初始权值矩阵是随机生成的,同时学习率η也是根据经验选取的,需要考察使用不同的初始权值矩阵和学习率是否都能得到正确的识别结果。为此,设最大训练代数G=2 000,随机生成1 000组不同的初始权值矩阵,在不同的学习率之下分别进行感知器训练和测试样本识别,得到的结果见表3。从表3中结果可以知道,对于不同的学习率和初始权值矩阵,2 000代之内感知器训练均能收敛,并且得到的感知器均能正确判断测试水样的类型。这与感知器理论中的经典结论[15]:线性可分问题总能在有限次训练之后收敛到一个稳定的权值矩阵,该权值矩阵确定的感知器能够实现正确的分类,是吻合的;但是从计算效率的角度考虑,学习率η取值过大或者过小,都会增大训练代数,增加计算量,故对焦作矿区突水水源识别问题而言,建议学习率η在区间[0.050,0.200]内选取。
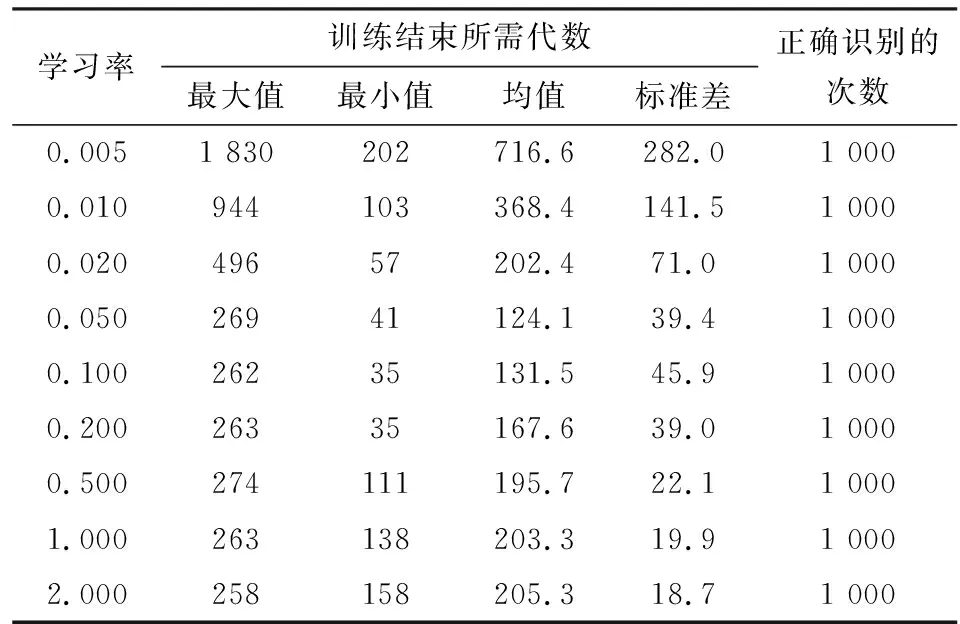
表3 不同学习率之下训练和识别的统计结果Table 3 Statistical results of training and recognitionunder different learning rates
3 结 语
构建了感知器模型进行焦作矿区矿井突水水源识别,应用结果表明,该水源识别问题是线性可分的,训练后的感知器能够正确判断突水水源;并且识别突水水源时不需要使用Na+和K+离子的浓度信息,这样处理在简化感知器模型结构的同时,有助于减小离子浓度检测的工作量,加快水源识别的速度。
与BP神经网络等更复杂的神经网络相比,感知器在结构上更简单,训练算法更容易实现,对于线性可分问题而言训练过程的收敛性有保证。为此在进行突水水源识别时,建议首先尝试使用感知器,并且在不损失识别能力的情况下应尽可能减少使用的水化学信息的种类;在感知器无法进行正确识别的情况下,再考虑使用更复杂的神经网络。

