充液航天器目标跟踪自适应控制*

梁 琼，岳宝增，于 丹

(北京理工大学宇航学院力学系，北京100081)

充液航天器目标跟踪自适应控制*

梁 琼，岳宝增，于 丹

(北京理工大学宇航学院力学系，北京100081)

对于在零重力环境下受到横向控制力和俯仰控制力矩作用的带球形贮液箱的航天器模型，研究了其在平面运动的动力学特性.将晃动液体等效为单摆模型，利用Lagrange方法建立了系统动力学方程并且将其转化为状态变量方程形式；应用微分几何原理，以单输入-单输出系统(SISO)为例，研究了系统的非线性动力学特性，并进一步针对目标跟踪问题设计了SISO系统基于线性化模型的控制策略.研究结果表明：对于液体晃动-航天器姿态耦合动力学系统采用极点配置间接自校正控制策略能够实现姿态角的镇定及跟踪.

充液航天器；姿态控制；自校正控制

随着航天事业的飞速发展，液体燃料占航天器总重量的比重不断加大，液体燃料的运动对在轨航天器的控制、定位和对接的影响都是关键性的［1］.因此充液航天器的建模及其姿态控制设计引起了广泛的关注.目前在国内外，有大量学者致力于研究这一问题.岳宝增［2］对单刚体充液航天器模型进行了姿态转换机动及控制研究.贾英宏、徐世杰［3］用变结构控制方法设计了充液挠性多体航天器的控制器.本文针对平面运动充液航天器采用Lagrange方法建立运动方程，研究SISO系统在平衡状态的线性化模型的非最小相位特性，采用极点配置间接自校正方法设计控制策略，达到姿态稳定和跟踪目的.

1 数学建模

1.1 航天器模型描述

本文研究在固定平面运动的充液航天器的动力学及控制问题，系统模型如图1所示［4-5］.假设航天器的球形燃料贮箱部分充液且整个系统处于零重力环境.将液体晃动等效为单摆模型并只考虑其一阶模态振动.设单摆的悬挂点位于球腔中心，其质量为mf、转动惯量为If，这些参数依赖于贮箱形状、液体特性及充液比.假设航天器(不包括燃料)的质量为m、转动惯量为I，其质心与单摆悬挂点在X方向的距离为b，摆锤质心与单摆悬挂点的距离为 a即单摆摆长.系统受到沿vx方向的持续推力Fc、横向控制力fc和在航天器质心的俯仰力矩M的作用.描述系统状态的变量为：轴向速度分量 vx，横截速度分量vz，航天器姿态角 θ(θ为轴向速度分量与坐标标架X轴的夹角)以及液体晃动角ψ.

1.2 运动方程

系统的动能：

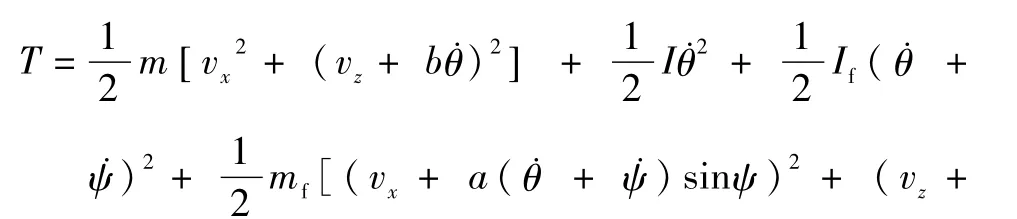
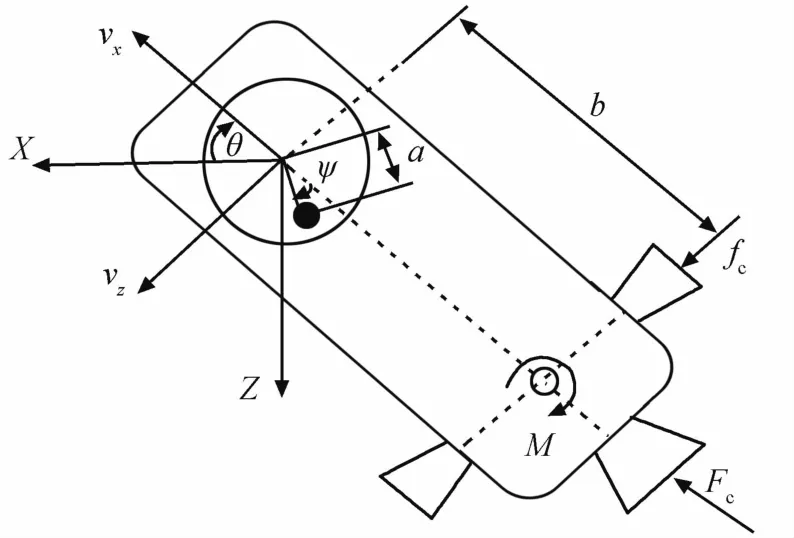
图1 充液航天器系统模型

忽略重力影响，故势能V=0.假定内部耗散作用由Rayleigh耗散函数定义，则

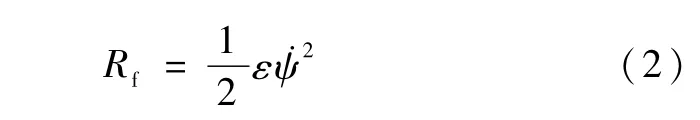
其中ε为耗散系数.通过求解Lagrange方程得到该充液航天器的非线性运动方程为

1.3 单输入-单输出系统描述

为简化起见，考虑单输入—单输出(SISO)系统，假设航天器系统仅受横向控制力fc作用.忽略阻尼因素影响，这样做不仅降低了公式推导及数值分析的复杂性，在实际工程中也是可行的，因为忽略阻尼后得到的结果更加保守.定义状态变量如下：

状态变量方程：

这里，u为系统输入fc，

其中，

系统输出h(x)=x1=θ.系统的平衡状态

求解上式，得到：

1.4 零动态分析

下面分析该非线性系统在平衡点处是否为最小相位系统.不失一般性，首先确定非线性系统在x0=［0 0 0 0］T处的相对阶 r.对输出求导，得：

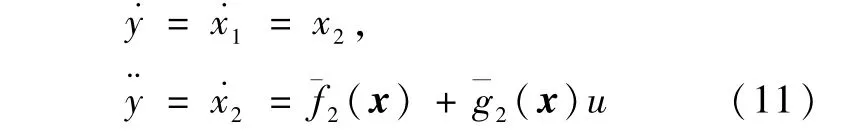
由此可知，系统的相对阶为r=2.根据非线性控制理论并通过计算李导数得到系统的零动态为

式中：

其中 u*(x)

下面需要确定零动态系统(12)在平衡点xze=［x3=0，x4=0］处的稳定性以判断该非线性系统是否为最小相位系统.为此需求解Jacobian矩阵并计算出它在平衡点xze处的值：

这里，

下面通过计算矩阵Jz(xze)的特征值来分析零动态的稳定性.因为

当Ia3c3mbFc+(I+mcb2)acFc(Ifbc)＜0时，得到特征根λ1，2=±，λ1，2∈R，这对应强不稳定情况.当λ1，2∈C时对应临界情况.为了验证理论分析的结果，进行数值模拟.系统参数取为m=600kg，I=720kg/m2，mf=100kg，If=90kg/m2，b=0.25m，a=0.32m，ε=0.19kg·m2/s，Fc=500N.数值模拟结果如图2所示，这里对应的是λ1，2∈C的零动态情况.从图2中看出，xe=［0 0 0 0］T为中心点，系统非渐近稳定，因此该非线性系统为非最小相位系统.由图2结果可知xe=［0 0 0 π］T为鞍点，系统非渐近稳定，即它是一个不稳定的平衡点.

2 线性化系统模型

不失一般性，在平衡位置

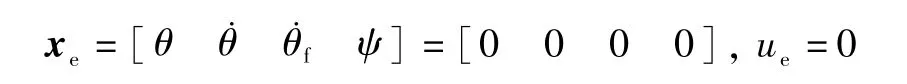
将系统线性化得到

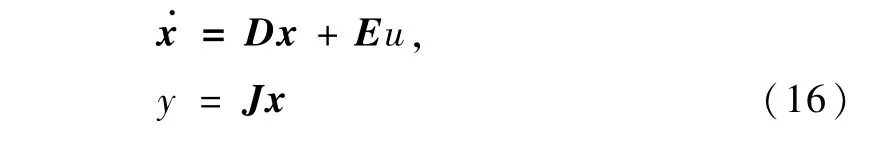
其中，

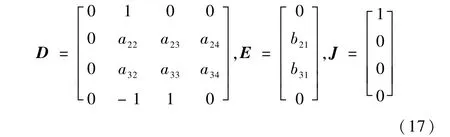
其中：

N=If(I+mcb2)+Icma2.

通过线性理论确定该平衡状态的线性模型是否稳定.首先由

计算得到特征值：

因此可知该线性化模型不稳定.

3 极点配置间接自校正控制器的设计

本文采用如下数学模型：

式中，y(k)和u(k)表示系统的输出和输入，ξ(k)和v(k)表示白噪声和有色噪声，d≥1为纯延时，且

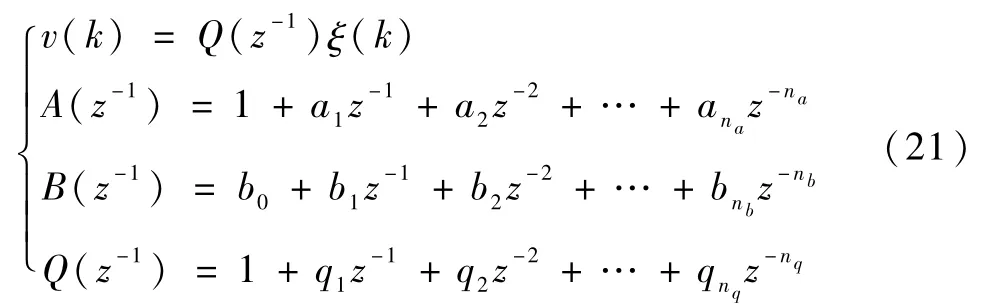
且A(z-1)和B(z-1)互质，即无公因子.

设计极点配置控制律(PPC，pole placement control)如下：

式中，F(z-1)、L(z-1)、G(z-1)是待定多项式，yr(k)为参考输入.于是，极点配置控制系统的结构如图3所示.则闭环系统的输出为

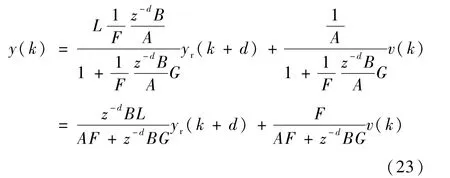
闭环特征方程为如下形式的Diophantine方程：

图3 极点配置控制系统结构图

极点配置控制的设计任务是：根据系统的固有特性和控制要求，来确定希望的闭环多项式T(z-1)，进而通过式(24)确定 F(z-1)、G(z-1)，最后由式(22)算出控制量.

设希望的输入输出表达式为

式中，Am(z-1)和Bm(z-1)分别为期望传递函数分母多项式和分子多项式，且两多项式互质.为了获得期望的输入输出响应，由式(23)及(25)得到：

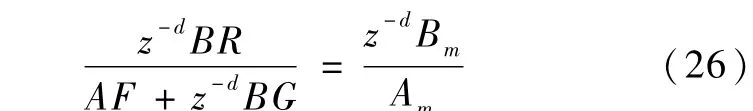
为保证Diophantine方程(24)有唯一解，令AF1和z-dB-G(B=B+B-，F=F1B+)的阶次相同，且等式右边阶次小于左边阶次，即要求各多项式的阶次满足下列关系(deg表示多项式的阶次)：

此外，为了保证控制律(22)是因果关系的，即控制器在物理上是可实现的，其必要条件为

上面介绍的极点配置控制方法是在假定被控对象参数已知的情况下，设计控制器多项式F、G和L，使得闭环系统的极点按希望的动态响应来配置.当被控对象未知时，则需进行自校正控制.极点配置设计方法有两种自校正控制，即间接自校正控制和直接自校正控制.本文采用间接自校正控制方法设计充液航天器目标跟踪控制策略［6］.设被控对象模型如式(20)所示，则可表示为

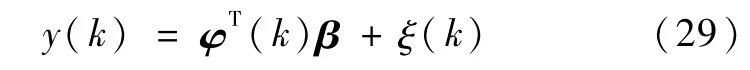
式中：其中模型结构na、nb、nq及 d已知.则参数估计可采用遗忘因子递推增广最小二乘法(σ为遗忘因子)，即

式中：

将系统状态方程转换为传递函数模型

经计算，

系统极点为

系统零点为s1=0.5578i，s2=-0.5578i.针对系统的非最小相位特点［7］，以及航天器含有不确定参数的情况，则可设计极点配置间接自校正控制算法以达到姿态稳定及跟踪目的.

假设期望闭环特征多项式为

期望输出为yr=sin(t).采用零阶保持器，并取采样周期Ts=2s对上述连续系统离散化后得

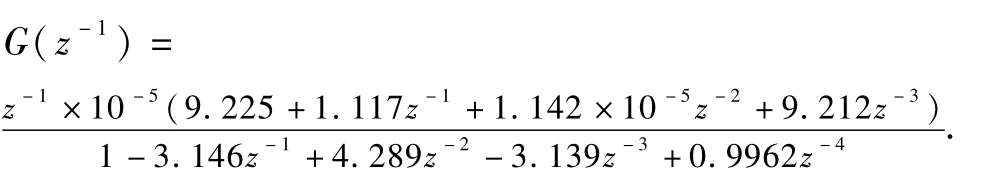
期待闭环特性离散得

取初值P(0)=106I，^β(0)=0.001，遗忘因子σ取为 0.98，初始条件取 x0=［0.002，0.00073，0，0.005］T.本文采用 MATLAB软件对所得系统进行数值仿真，数值结果如图4～7所示.其中，图4为线性系统APPC跟踪效果图，图5为输入u(t)的时间历程图，图6为状态变量˙θ的时间历程图，图7为液体燃料晃动角ψ的时间历程图.数值仿真结果表明该方法对充液航天器目标跟踪控制的有效性.

图4 线性系统APPC跟踪效果图

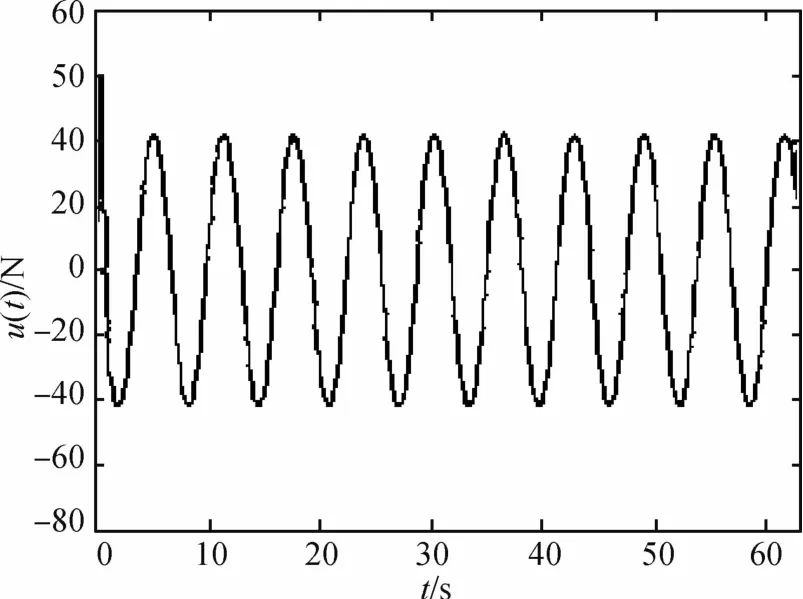
图5 输入u(t)的时间历程图

图6 状态变量˙θ的时间历程图

4 结 论

本文研究了充液航天器姿态动力学建模及控制问题.采用球摆等效力学模型模拟液体晃动动力学并采用Lagrange方程推导了液体晃动及航天器耦合系统的动力学方程.采用现代微分几何理论对非线性耦合系统进行了零动态分析；在SISO系统线性化模型下采用极点配置间接自校正控制策略实现了姿态角的镇定及跟踪.研究结果表明：对于液体晃动航天器姿态耦合动力学系统采用极点配置间接自校正控制策略能够实现姿态角的镇定及跟踪.得到的结果具有理论意义和工程应用价值.

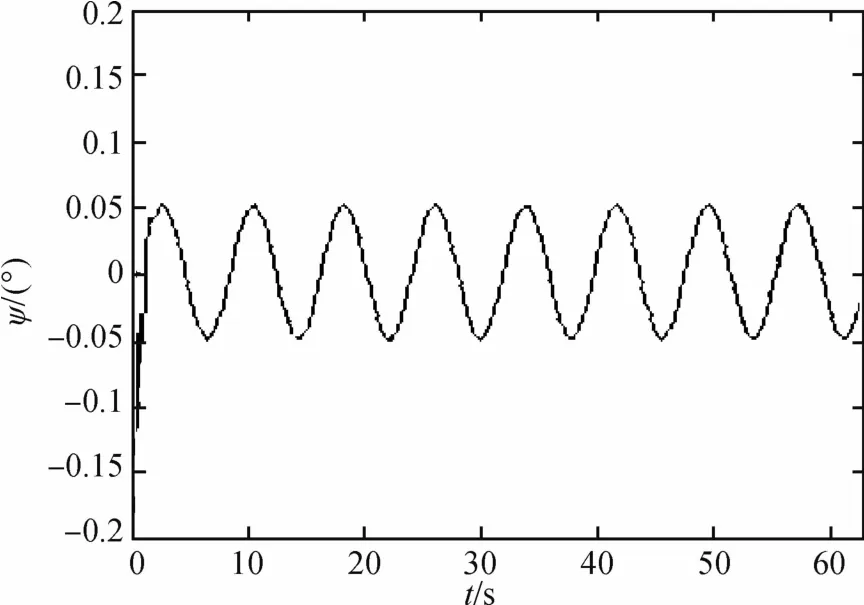
图7 液体晃动角ψ的时间历程图

［1］尹力中，王本利，邹经湘.航天器液体晃动与液固耦合动力学研究概述［J］.哈尔滨工业大学学报，1999，31(2)：118-122

［2］岳宝增.充液自旋航天器姿态转换机动及控制研究［J］.动力学与控制学报， 2008，6(2)：118-121

［3］贾英宏，徐世杰.充液挠性多体航天器的变结构控制［J］.宇航学报， 2002，23(3)，18-23

［4］Cho S， McClam roch N H， Reyhanoglu M.Feedback control of a space vehicle with unactuated fuel slosh dynamics［C］.AIAA Guidance， Navigation， and Control Conference， Denver， CO， August 14-17，2000

［5］Reyhanoglu M.Maneuvering control problems for a spacecraft with unactuated fuel slosh dynam ics［C］.IEEE Conference on Control Applications， Istanbul，June 23-25，2003

［6］奥斯特隆姆 K J，威顿马克 B.自适应控制［M］.李清泉译.北京：科学出版社，1992

［7］Slotine JE，LiW P.应用非线性控制［M］.程代展译.北京：机械工业出版社，2006

Adaptive Control of Target Tracking for Liquid-Filled Spacecraft

LIANG Qiong， YUE Baozeng， YU Dan
(Department of Mechanics， School of Aerospace Engineering，Beijing Institute of Technology， Beijing 100081，China)

For the spacecraftmodel with a spherical fuel tank controlled by a horizontal force and a pitch moment under the condition of the zero gravity，the dynamics performance about a liquid-filled spacecraft moving in a plane is studied.W ith the single pendulum model of a typical spacecraft with fuel sloshing，the dynam ics equations are derived based on Lagrange method，and then are transformed into the form of state variable equations.In the case of single input-single output(SISO)，the nonlinear dynamics characteristics of the system are discussed by means of the differential geometry theory.Furthermore，a control strategy for the target tracking is designed on the basis of linearization model of SISO system.The result indicates that the pole placement-based indirect adaptive control strategy can realize attitude stabilization and tracking for liquid sloshing-spacecraft attitude coupled dynamics system.

liquid-filled spacecraft； attitude control；self-tuning control

V448.22+3

A

1674-1579(2011)01-0040-05

10.3969/j.issn.1674-1579.2011.01.009

*国家自然科学基金(10772026，11072030)资助项目.

2010-10-06

梁 琼(1986—)，女，陕西人，硕士研究生，研究方向为充液航天器动力学与控制(e-mail：liang-qiong501@163.com).