过载约束下的探月飞船再入轨迹的在线设计
李贵明,刘良栋
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
过载约束下的探月飞船再入轨迹的在线设计
李贵明1,2,刘良栋1
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
研究了以第二宇宙速度返回地球的载人探月飞船的再入制导律设计问题.针对基于落点分析的数值预测-校正算法不能有效满足再入过程的气动过载约束条件的问题,提出一种基于解析计算的常值气动过载算法与基于数值积分的预测-校正技术相结合的融合再入制导方案,在线生成了同时满足过载约束和落点精度要求的再入轨迹.数值仿真表明提出的制导算法不仅能满足达到高精度着陆的要求,还能满足气动过载约束要求.在一定的再入初始条件下,探月返回飞船可以不必采用逻辑复杂的阿波罗式跳跃再入方案.这一方案可为即将展开的载人探月活动制定月-地返回轨道和再入策略提供参考.
探月返回飞船;气动过载;预测-校正制导;常值过载制导;综合制导策略
自2004年美国提出轰动全球的“太空探索新构思”[1]计划后,新一轮太空探索竞赛的帷幕渐渐拉开.目前,美国正在“星座计划”的框架下,加紧研制新一代载人宇宙飞船—成员探索飞行器(CEV),即猎户座(Orion).俄罗斯也推出自己的联盟号载人飞船的接替者—快船号(Kliper).欧空局、日本和印度等也在加紧步伐,开始新一轮的探月竞赛[2].
中国于2007年成功发射了嫦娥一号卫星,标志中国的探月工程进入了实践阶段.随着中国航天技术的进步特别是载人航天事业和嫦娥工程的成功,有必要制定未来载人探月的相关设想和初步方案,为即要开展的载人探月工程奠定必要技术基础.
大气层内的气动减速是返回过程中的关键阶段,而制导、导航和控制分系统是此过程的中枢,负责再入飞船的姿态控制、轨迹规划和轨迹跟踪等核心技术.一般来讲,再入制导方法分为两大类,即标准轨道法和预测制导法.其中,预测制导法是以消除实际轨道的预报落点和预定落点之间的偏差为目的的制导方法,该方法是在计算机内存储理论落点的特征参数,根据导航平台测量的飞行器的实际状态参数,实时进行落点计算,并将计算的结果与理论落点进行比较,形成的误差控制信号输入到计算机的制导方程,然后按照既定的制导规律控制倾侧角,以实现精确着陆[3].
文献[4]针对探月返回的低升力再入飞行器,设计了轨迹规划和闭环制导相结合的预测—校正方法.在轨迹规划阶段,寻求满足纵向航程条件的倾侧角幅值,从而借助于数值预测方法,将一个单输入非线性系统的控制问题,转化为单变量非线性方程的寻根问题.文献[5]提出一种 Motion Primitives算法和邻近最优控制算法,有效解决了航天飞机的靠近和着陆问题,并研究了任务失效情况下的在线轨迹重构问题.针对航天飞机的再入制导问题,文献[6]提出了一种嵌入路径约束控制策略的预测—校正算法,利用数值积分运算设计出了一种同时满足末端约束和路径约束的制导策略.
南英等[7]研究了多种不同条件下的最优返回再入飞行轨迹设计问题.从热量的角度指出,跳跃式再入比直接再入具有更好气动加热环境和更小的最大气动热流密度,因此更适用工程实践.陆平等[4,8,9]认为,当执行探月返回再入任务飞行器需要实现大飞行纵程时,跳跃式再入是唯一可行的方案.
直接利用基于落点分析的预测-校正再入制导算法设计的探月飞船再入轨迹,存在着过载峰值过大的问题.为此,本文利用数值预测算法得到的过载超限信息,引入基于解析算法的常值气动过载减速步骤,生成恒定气动过载减速制导律.当后续飞行中的预测过载满足要求时,将制导逻辑切换回基于落点预报的校正制导算法,直至达到开伞点高度.最后,对于给定的初始再入条件和终端要求,利用本文设计的融合制导算法能够在线生成探月飞船再入轨迹.而且,本算法能统一处理有无跳跃阶段的再入轨迹规划问题,具有在线生成再入轨迹的能力,且能同时满足落点精度要求和气动过载的约束.
1 模型和问题
1.1 再入飞船质心动力学
低升阻比的再入飞船以配平攻角飞行时,处于瞬时平衡状态,此时的控制变量为倾侧角ζ[3].飞船再入制导的目标即规划合理的倾侧角指令,使飞船沿着满足各种路径约束的再入轨迹,精确着陆于指定区域.为保证航天员生命安全,必须设计满足过载要求的再入轨迹.
建立在地理坐标系的再入动力学方程使用了一定的简化和假设,适用于初步设计再入轨道.这些基本假设有:地球是标准球体;航天器是质量为m的点质量再入器;航天器仅受空气动力和行星引力作用.飞船再入动力学方程为[10]
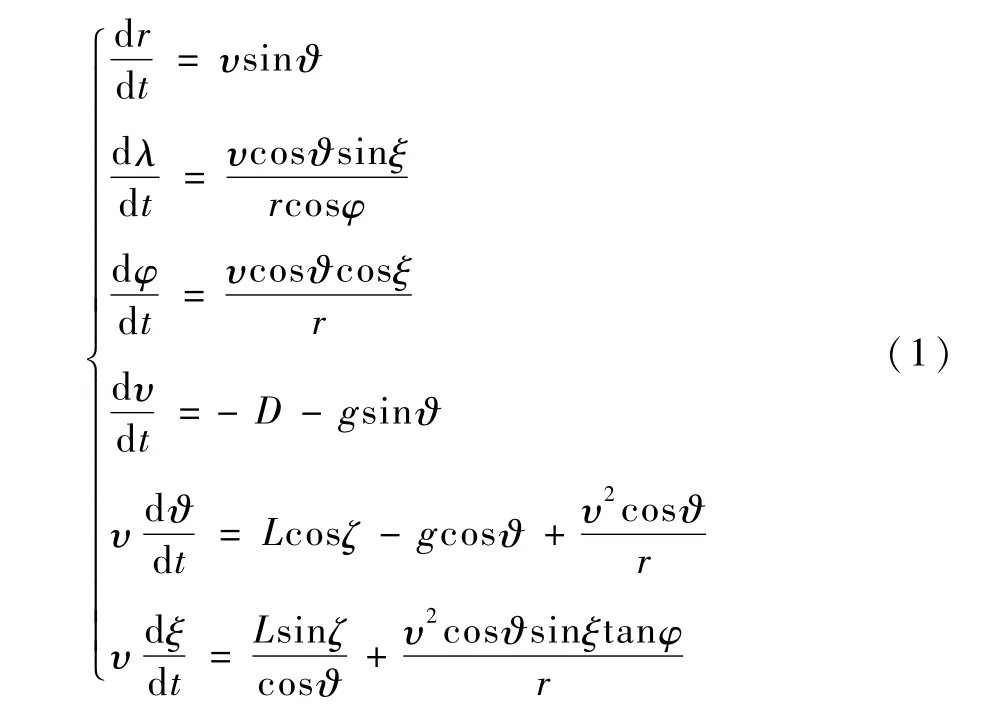
式中,r为地心距,λ为经度,φ为纬度,υ为速度,ϑ为飞行路径角,ξ为速度方位角,g为重力加速度.升力加速度L和阻力加速度D为上面两式中ρ为大气密度,S为飞船参考面积,m为飞船质量,CL为升力系数,CD为阻力系数.
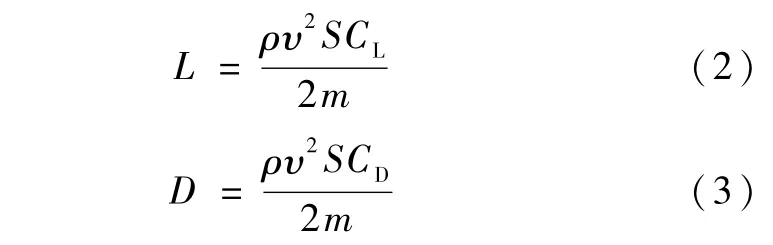
1.2 问题描述
在式(1)中,控制变量为飞船倾侧角ζ.本文的设计目标可以描述为:在一定的初始再入条件下,实时规划合理的再入倾侧角指令,使得在线生成的再入轨迹满足一定的气动过载要求,同时保证飞船的落点精度要求.
2 再入制导算法
本节首先简要介绍预测-校正制导方法.针对其不能满足过载约束条件的问题,我们研究并推导了常值气动过载再入制导算法,给出了倾侧角指令的表达形式.将常值气动过载算法和预测-校正算法相结合,生成能同时满足过载约束和着陆点精度要求的再入轨迹.
2.1 预测-校正再入制导
基于数值计算的预测—校正制导法,利用当前的飞行条件,数值积分再入方程,利用落点预报进行倾侧角指令的修正,在线得到一条满足落点精度要求的再入轨迹[11-12].下面详细给出预测—校正再入制导的基本设计步骤.
在给定的倾侧角指令ζ1作用下,利用当前状态信息,积分飞船质心动力学方程,直到飞行高度h满足

得到开伞点的经纬度分别为λf和φf.式(4)中h0为开伞点高度.h=r-R,R为地球半径.于是得到由当前积分位置(λ,φ)到开伞点的纵向航程(预测纵程)为

式中β由下式得到
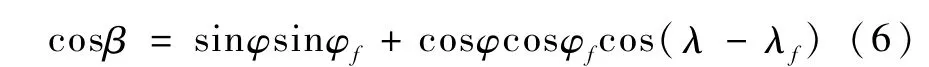
同理,可以利用公式(5)和(6)计算得到从当前位置到目标开伞点(λ0,φ0)的纵向航程 R0.那么在给定的倾侧角指令下,纵程的预测误差Rr为

如果Rr大于落点误差上限值,则采用适当的调节机制改变倾侧角指令值,重复计算上述步骤,直到得到适当的指令ζ1.如果Rr处于落点精度误差范围内,则认为此时的倾侧角指令ζ1是合适的,即将此指令ζ1发送给飞船控制系统.下一个预测阶段重复上述步骤.
在进行纵向航程预测时,由于 L cosζ与倾侧角指令的符号无关,因此,上述纵向制导过程仅能决定倾侧角指令的幅值.对于倾侧角指令的符号,由下述的横向制导策略[3]决定.
由于倾侧角指令的符号决定了升力的方向,因此可以控制飞船的横向运动轨迹.一般选取飞船再入速度υ为变量,设置横向航程约束Zs为一个漏斗形的边界,即
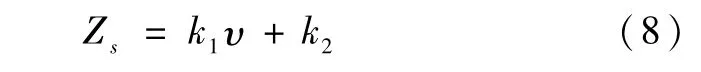
式中k1和k2为待设计常数.可见,边界Zs随着再入速度减小而减小.当实际横向航程的幅值达到漏斗边界值时,立刻改变倾侧角指令的符号,从而改变升力的方向,达到减小横程误差的目的.
当需要调整倾侧角指令幅值进行纵向航程制导时,本文借鉴文献[4]的研究成果,即利用正割法调整倾侧角指令的幅值,其迭代关系式为
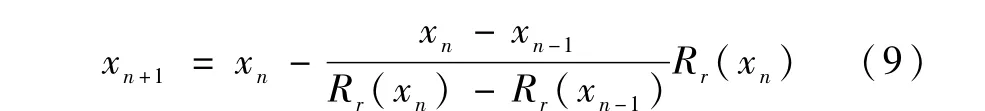
式中 xn=cosζn.
2.2 常值气动过载再入制导
设飞船的飞行高度为h,由式(1)可知
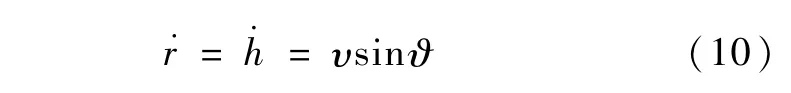
式(10)对时间求导,可得
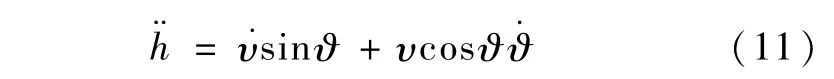
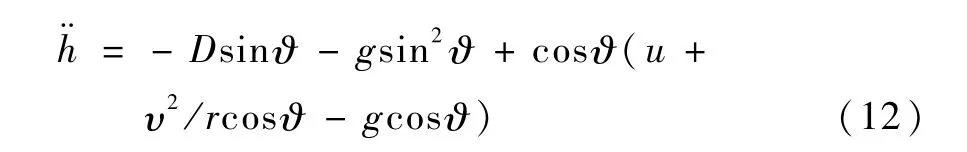
式中 u=L cosζ.
设大气密度ρ是高度的指数函数,即

式中ρ0和 β为常值.对式(13)求导,得
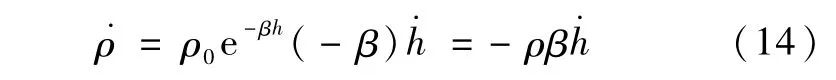
对式(3)求导,则有
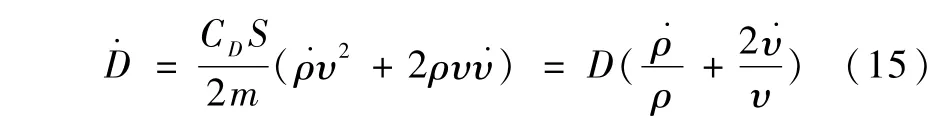
综合式(1)和式(14),得到
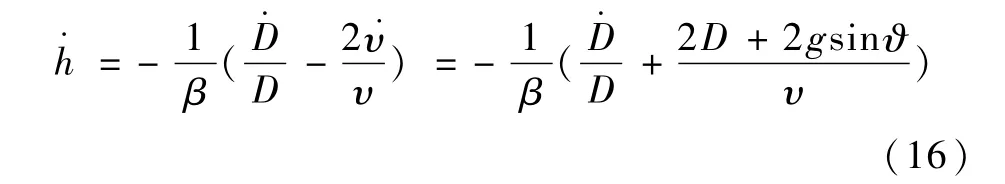
考虑到气动过载表达式为
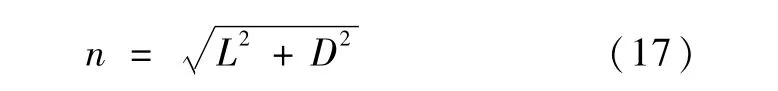
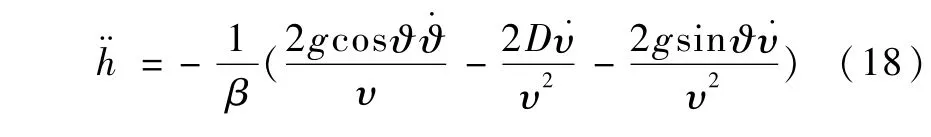
考虑到式(1),可得
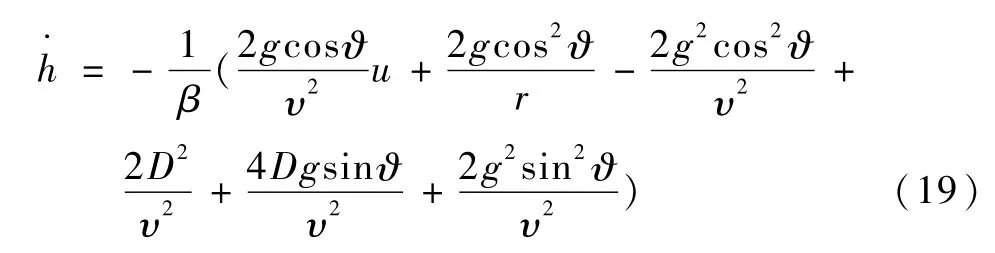
将式(12)代入式(19),即可解得纵向平面内的升力加速度控制量u,即
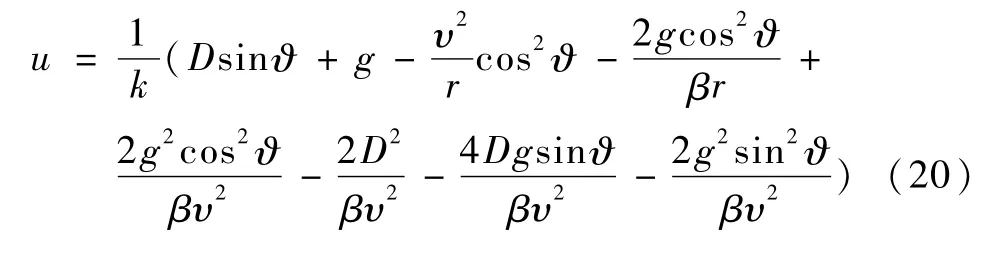
那么,维持飞船沿着常值气动过载飞行时所需的倾侧角指令幅值ζ2为
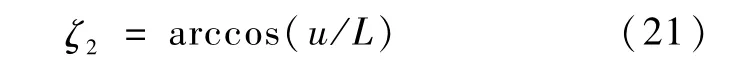
2.3 融合制导策略
融合制导策略首先启动基于落点分析的预测—校正,预测整个再入飞行过程中是否存在气动过载超标问题.当预测过载超出过载约束,即
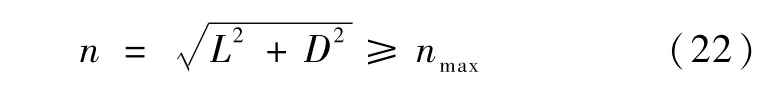
即需要引入常值过载制导算法.通过常值过载制导算法,选取适当的再入倾侧角指令,使飞船沿恒定过载轨迹再入,并实时进行系统状态的更新.持续常值过载制导过程减速飞行,每间隔一定时间(本算法选择10s)开启一次预测—校正算法预测后续飞行中的过载,直到预测到的后续气动过载峰值小于指标要求的nmax为止.然后将制导逻辑切回预测—校正制导算法,直至达到开伞点,结束再入轨迹规划任务.图1详细地描述了融合制导策略的流程.
注1.融合再入制导算法的目的在于采用允许的最大气动过载进行减速飞行,即以允许的最大制动消耗再入飞船的能量,使得后续的预测-校正制导算法不会再引入超出约束的气动过载幅值.当出现极端的再入条件,例如利用式(20)计算得到的u为

时,飞船无法提供必要的升力,因此,只能采用最大升力状态过载飞行,即ζ=0.由此可见,融合再入制导算法仅能在一定初始再入条件范围内解决过载约束问题.
注2.融合再入制导算法能在线设计出同时满足气动过载和着落精度要求的再入轨迹,但数值积分运算对船载控制计算机的运算能力提出了较高的要求.
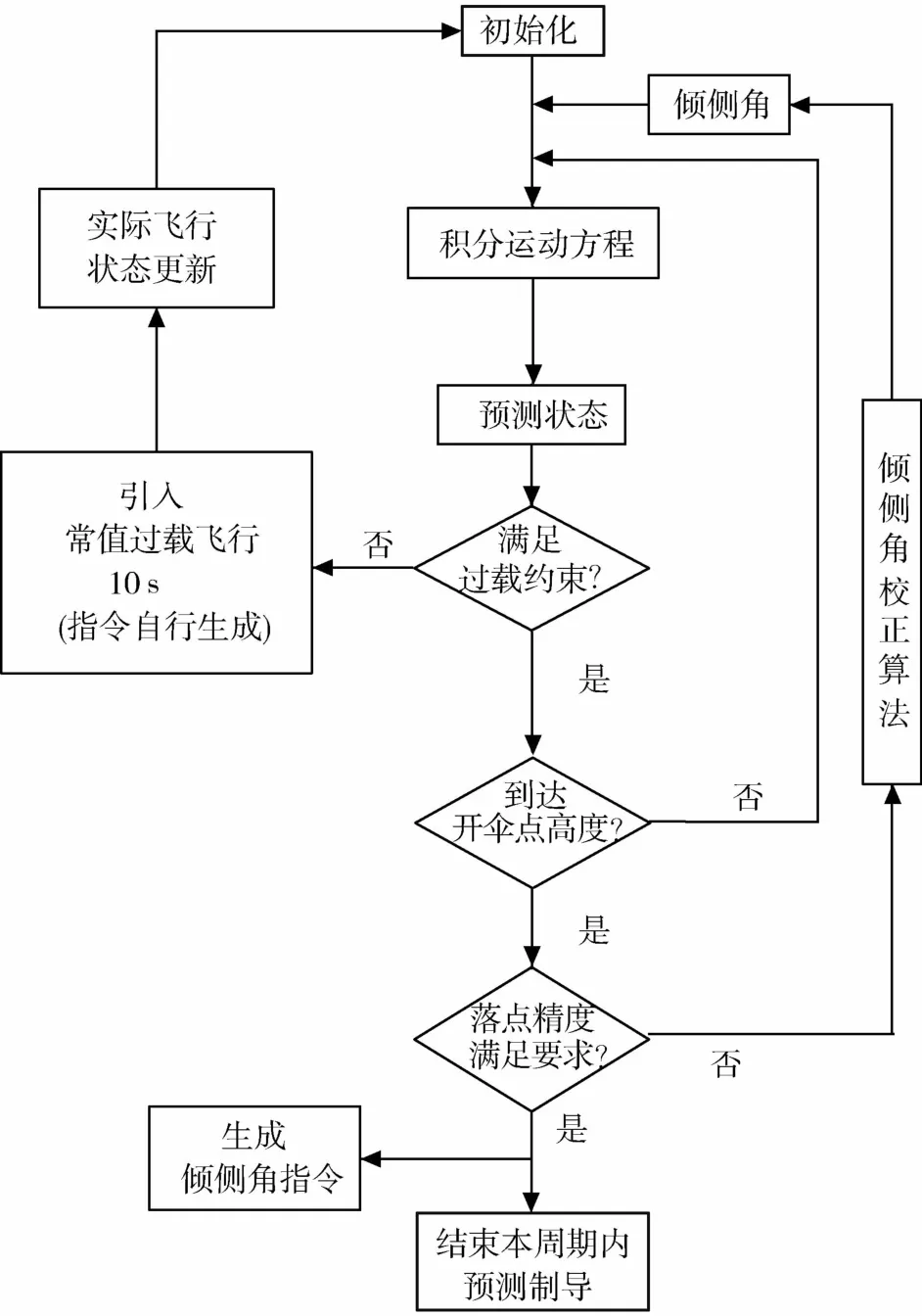
图1 融合算法的流程示意
3 数学仿真
设飞船的再入初始条件为:再入初始高度80km,初始速度为11.032km/s,再入点经度为东经118.5°,北纬 11.0°,初始飞行路径角为 -3.8255°,初始速度方向角为 3.3687°.开伞点距地面高度10km,位置为东经 112.1°,北纬 42.3°.设定最大气动过载指标nmax为4.5g.针对本文的初始条件,再入初期预测出存在过载超标(6.3g)后,在再入初期给定0°倾侧角指令幅值,然后向飞船发出此指令,直到飞行至最大过载(4g).从此刻起,引入常值过载算法,使飞船以常值过载状态再入飞行,每10s运算一次预测-校正制导算法,直到预测的气动过载峰值满足约束条件为止.然后启动预测—校正算法,直至飞行任务结束.仿真结果如图2~5所示.
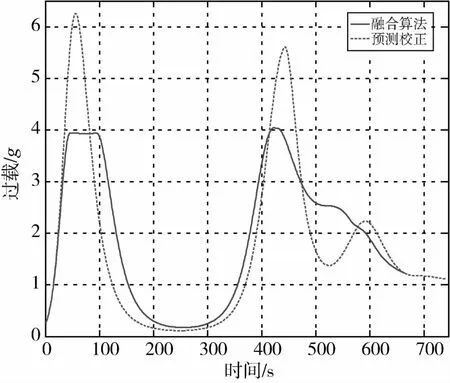
图2 探月飞船的再入过载值
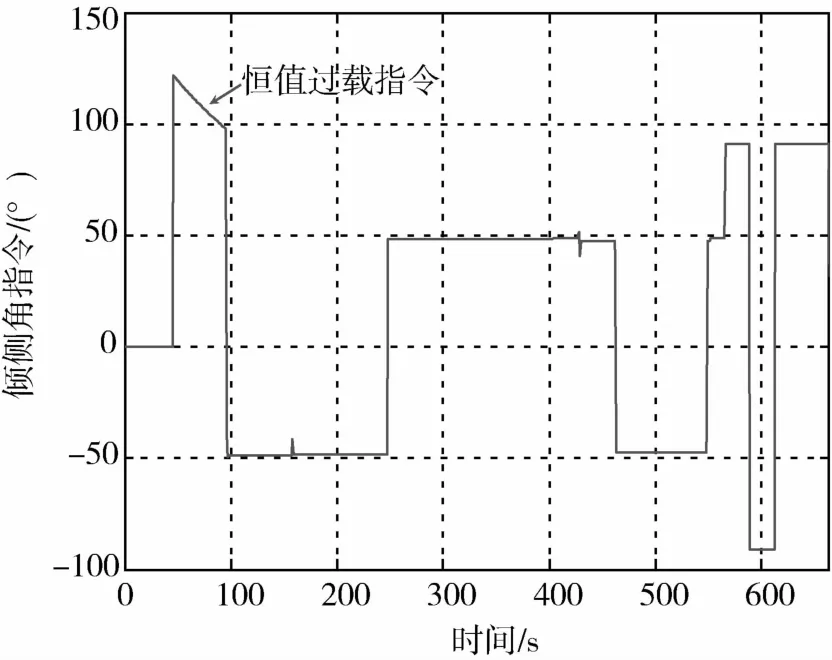
图4 探月飞船的再入倾侧角指令
图2中的虚线描述了仅利用预测—校正算法时的再入过载.由曲线可知,再入过程的最大过载超出了指标要求,峰值达到了6.3g,并且超标情况前后出现两次.融合制导策略描述的再入轨迹的过载由图2中的实线表示.由仿真曲线可知,融合了恒值过载限制的预测—校正算法,保证了在再入峰值将超出要求时,通过调整初期和前期倾侧角指令使过载值处于设计恒定值附近,有效解决了再入峰值过大的问题.
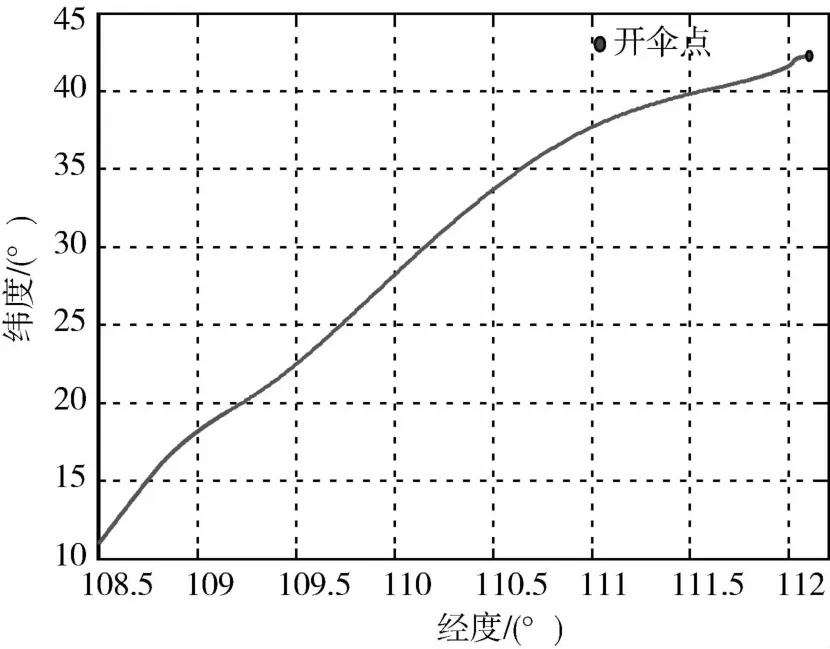
图5 探月飞船再入的星下点轨迹
图3和图4分别描述了再入倾侧角指令和再入飞行高度,其中倾侧角符号在整个再入过程中反转了6次;再入飞行高度存在着跳跃的趋势,但并没有弹出大气层.事实上,当再入航程相对较小时,就会出现跳跃阶段.图5描述了飞船再入飞行的星下点轨迹,计算结果表明开伞点的精度约为0.5km.
仿真结果证实,飞船的再入结果满足过载约束和着陆精度要求,说明结合恒值过载与预测—校正法的融合制导策略对于存在过载约束的探月飞船的再入轨迹在线设计问题有效.
注3.本文的算法采用三自由度的质心再入动力学模型,因此没有考虑到飞船姿态调节过程,即倾侧角指令的翻转过程对再入轨迹规划的影响.因此,适用于再入轨迹的初步设计.预测-校正制导的在线能力保证了本文算法在大气密度摄动、初始条件偏差和风速影响条件下仍然有效.
注4.跳跃式再入比直接再入具有更好气动加热环境[7];当执行探月返回再入任务飞船需要实现大飞行纵程时,跳跃式再入是可行的方案[8].但跳跃式再入一般涉及到复杂的逻辑过程,较弹道式再入的工程实践难度大.实际上,跳跃式再入方案最终也没有用于阿波罗飞船的探月返回飞行任务.本文的算法的优势还在于可根据系统的实际条件在线规划再入轨迹,统一处理含跳跃阶段和不含跳跃阶段的情形.根据仿真结果可知,适当的月地返回轨道设计方案将带来良好的再入初始条件,更利于再入制导律的优化设计.
4 结 论
探月返回飞船具有再入初始速度大、气动过载严重的特点,要求针对这些问题提出行之有效的再入制导算法,控制飞船沿着合理的再入轨迹抵达预定的开伞点.本文在采用合理的近似假设的前提下,提出了基于解析计算的恒值过载算法和基于数值积分预测—校正算法相结合的融合制导策略,能有效解决探月飞船的再入制导问题,可保证飞船控制系统能在线设计同时满足过载要求和着陆精度要求的再入轨迹.仿真结果说明了本文方法的有效性.从过载的角度看,在一定的再入初始条件下,探月返回飞船可不采用跳跃式再入.
[1]Bush G W, Remarks at the national aeronautics and space administration [J].Week ly Compilation of Presidential Documents, 2004, 40(3): 66-68
[2]魏晨曦.美国“猎户座”飞船新进展[J].国际空间,2007(1):5-8
[3]赵汉元.飞行器再入动力学和制导[M].长沙:国防科技大学出版社,1997
[4]Brunner CW,Lu P.Skip entry trajectory planning and guidance[J].Journal of Guidance, Control and Dynam ics, 2008, 31(5): 1210-1219
[5]Jiang Z S,Ordonez R.On-line robust trajectory generation on approach and landing for reusable launch vehicles[J].Automatica, 2009, 45(7): 1668-1678
[6]Joshi A,Sivan K.Predictor-corrector reentry guidance algorithm with path constraints for atmospheric entry vehicles[J].Journal of Guidance, Control and Dynamics, 2007, 30(5): 1842-1847
[7]南英,陆宇平,龚平.登月返回地球再入轨迹的优化设计[J].宇航学报,2009,30(5):1842-1847
[8]陆平,朱亮,敬忠良,胡世强.探月返回跳跃式再入制导[C].第十三届空间及运动体控制技术学术年会,武夷山,2008
[9]Lu P.Predictor-corrector entry guidance for low-lift vehicles[J].Journal of Guidance, Control and Dynamics, 2008, 31(4): 1067-1075
[10]王希季.航天器进入与返回技术(上)[M].北京:宇航出版社,1991
[11]胡军.载人飞船一种混合再入制导方法[C].第八届空间及运动体控制技术学术年会,黄山,1998
[12]李惠峰,张蕊.探月飞船预测-校正再入制导律设计[J].空间控制技术与应用,2009,35(1):19-24
On Line Design of Reentry Trajectory under Aerodynam ic Acceleration Load Constraint of a Lunar Vehicle
LIGuiming1,2, LIU Liangdong1
(1.Beijing Institute of Control Engineering, Beijing 100190,China;2.Science and Technology on Space Intelligent Control Laboratory, Beijing 100190,China)
In this paper a guidance algorithm is presented to address the reentry problem of a lunar returning vehicle at the second cosmic velocity.The predictor-correctormethod based on the accurate landing target location cannot meet the aerodynam ic acceleration load constraint in general.For this technical problem,we combine the predictor-corrector method and a constant acceleration load method,and propose an integrated reentry guidance strategy.The improved scheme is based on real-time trajectory planning and generates a feasible trajectory during the reentry flight,thus satisfying both term inal path constraint and aerodynam ic load constraint.Numerical simulation results are presented to demonstrate the effectiveness of the proposed scheme.It is shown from this presented study that if the initial reentry condition is selected appropriately,the skip trajectory entry guidance algorithm may not use the Apollo's scheme which has a very comp licated logical technique.This work is of benefit to the design ofmoon to earth trajectory and the reentry strategy of our upcom ing manned moon landing project.
lunar returning vehicle; aerodynam ic acceleration load; predictor-corrector guidance; constant acceleration load guidance;integrated guidance strategy

V448.235
A
1674-1579(2011)01-0006-05
10.3969/j.issn.1674-1579.2011.01.002
2010-07-10
李贵明(1983—),男,黑龙江人,博士研究生,研究方向为航天器姿态控制、协同控制理论与应用(e-mail:hitlgm@gmail.com).

