基于ANSYS Workbench的直齿轮接触分析

周钊

（湖北汽车工业学院 汽车工程系，湖北 十堰442002）

齿轮广泛地应用于汽车、拖拉机、工程机械等产业。现代机械设计对齿轮传动提出了越来越高的要求，齿轮传递扭矩过程中，齿轮的接触疲劳强度是评价齿轮承载能力的一个重要尺度，如果齿面接触强度不够，齿面将产生点蚀、剥落、塑性变形等损伤，为了防止齿面产生这些损伤，必须进行齿面的接触强度计算。本文使用ANSYS Workbench有限元分析软件，建立齿轮接触仿真分析模型。分析计算了1对直齿轮的接触应力，将理论赫兹应力结果与有限元结果比较，说明有限元法仿真齿轮类问题的精确性和可靠性。

1 齿轮三维网格模型

利用CATIA软件建立1对圆柱直齿轮的几何模型，齿轮参数如表1所示，将几何模型保存为STP格式，将其导入Workbench软件中。为使齿轮副得到较规整的网格，将齿轮分割成如图1所示的若干部分。

表1 1对直齿轮几何参数

齿轮接触处应力变化急剧，需要设定较密网格，而远离关注部位的非接触区域，改用较大尺寸的单元作为近似写照。基于上述认识，再次在齿轮接触处进行切割，分割区域的半径为0.47mm，该范围包含齿轮的接触区域，如图2所示。

小齿轮的材料为 40 Cr，其弹性模量 E1为206GPa，泊松比μ1为 0.28；大齿轮的材料为45号钢，其弹性模量E2为216GPa，泊松比μ2为0.3。一个优良的有限元离散模型应该具有足够多的单元数目、合理的单元布局以及品质优良的单元形态。为建立合理的有限元模型，整个齿轮模型采用扫掠网格划分方式，通过8节点6面体单元（SOLID185）来离散，将齿轮副结构分为接触区域，接触轮齿和非接触轮齿3个部分，采用不同的网格密度，其中接触区域的网格最小，网格尺寸为0.01mm，网格模型如图3～4所示。齿轮副有限元模型节点数170152，单元数151556。

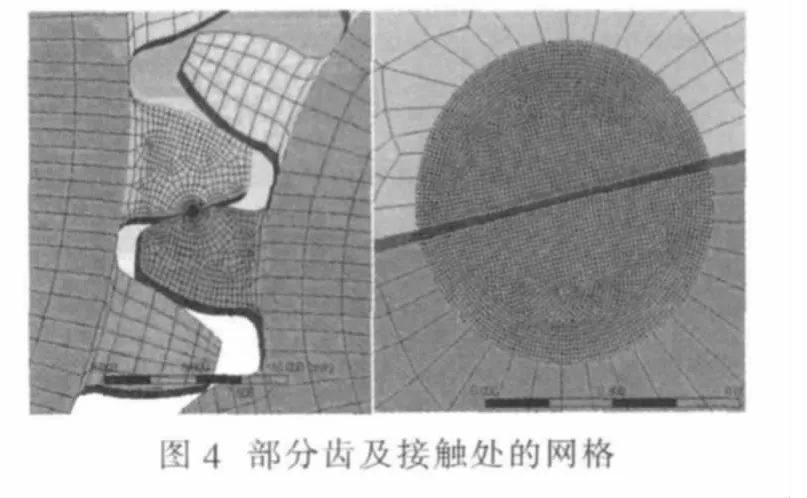
2 形成接触单元

接触问题都是非线性问题，它们的求解需要占用大量的计算机资源。因此，理解问题的物理特性和为了使运行足够高效而花时间建立模型，这些是很重要的。接触问题分为两大类：刚性到柔性接触类、柔性到柔性接触类。本课题研究的是柔性到柔性的接触类问题，有限元程序支持柔性对柔性的面到面接触单元，目标面一般是较刚表面，该表面在3维问题中用TARGE170单元来模拟，一般情况下，小齿轮表面刚度比大齿轮表面刚度大，所以此处的目标面为小齿轮齿面。选择大齿轮的齿面为接触面。接触单元采用Contact174单元，所谓的接触对，都通过1个共同的实常数来定义。本文共形成接触单元2058个。

本文采用增强拉格朗日算法计算齿轮接触，增强拉格朗日算法在纯罚函数的基础上引入接触力的参量，相比罚函数而言对接触刚度的依赖不太敏感，接触力的引入能减少渗透量，但势必进行更多的迭代才能得到收敛的结果。

接触刚度的选择是接触问题计算的难点［4］，由于得到一个最佳的接触刚度是很困难的，经常有一些棘手的问题。利用低的参数会导致大的误差，利用大的刚度值虽然会得到比较小的误差，但会诱发有限元模型不稳定。为确定合适的接触刚度系数，应该从较小值开始，不断增大进行多次试算，直到接触应力变化较小为止。不同接触刚度的数值模拟在后文中讨论。

3 边界条件及仿真结果

3.1 边界条件

小齿轮受到的驱动扭矩T为20000N·mm，约束小齿轮内圈所有节点径向和轴向的自由度。此外对大齿轮内圈所有节点施加全约束。加载后模型，如图5所示。

3.2 仿真结果

接触问题是非线性行为，ANSYS Workbench采用牛顿—拉普森算法进行计算，取接触刚度系数为1，摩擦系数为0，计算后接触应力图如图6所示，最大接触压力602.5MPa，发生在初始接触点处，沿齿宽方向不变，沿接触齿面方向逐渐递减。MISES应力图如图7所示，最大MISES应力为375.8MPa，发生在齿轮端面接触点处，最大切应力图如图8所示，最大切应力的最大值为208 MPa，发生在初始接触点的下方，并没有发生在接触表面上。这是与接触力学的理论计算相符的。齿轮的周向变形云图如图9所示，最大值为0.0281 mm。

4 齿轮接触传统理论计算

渐开线齿轮齿面为形状较为复杂的曲面。然而由于接触区宽度远小于齿面在接触点的曲率半径，因而可对啮合齿面做适当简化［1］。实验结果表明：当运转条件相同时，齿轮间的接触状态可用1对圆柱体来模拟，1对齿轮之间的啮合可转换为2个圆柱体沿其母线的接触，两圆柱体的半径分别与啮合点大小齿轮的齿面曲率半径相等。基于上述认识，齿轮接触的接触应力可近似用2个圆柱体接触压力公式计算［2］，即

式中：ZE为弹性影响系数，

E1，E2和 μ1， μ2分别为直齿轮副的弹性模量和泊松比，ZH为区域系数，

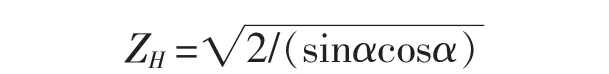
α为压力角；b为齿宽；T为小齿轮所受扭矩；d1为小齿轮分度圆直径；K为载荷系数，为使理论解与有限元解对比，而齿轮副模型属静力分析，故载荷系数取1；u为大小齿轮齿数比。

将本文各物理量数据代入式（1），计算得直齿轮副的最大接触应力为736.8 MPa，最大切应力表达式为max为0.3σH，最大切应力的理论解为221MPa。最大接触应力和最大切应力的理论解与有限元解误差很大。一般来说，小的接触刚度会导致大的穿透深度，会产生较大的误差。增大接触刚度来抵抗穿透，使有限元仿真结果更可靠。

5 不同接触刚度的有限元分析结果

接触分析中，接触刚度的确定是重点，也是难点，尤其法向接触刚度因子对计算的结果影响很大［3］。一般来讲，首先预估低的接触刚度，并检查穿透，然后随着增大接触刚度接触穿透不断减小，接触计算结果也就愈精确，直至接触结果变化不大为止。表2为不同法向接触刚度因子的有限元计算结果。由表2可知，接触刚度增大，最大接触应力和最大切应力在不断增大。当接触刚度系数大于20时，计算时间和迭代次数明显增加。本文取接触刚度系数为20时为理想的接触刚度。最大接触应力和最大切应力的有限元解与理论解的计算误差分别为2.9%和1.7%。

表2 不同接触刚度的有限元分析结果

6 结 论

接触刚度的确定是接触分析的重点和难点，可采用数值递推法确定合适的接触刚度。

创建精细的齿轮接触有限元模型，检测误差并不断修正有限元模型，能使齿轮接触问题的有限元解更可靠，比传统赫兹理论近似计算更精确。

［1］ Johnson K L.接触力学［M］.徐秉业，罗学富，刘信声，等译.北京：高等教育出版社，1992.

［2］ 濮良贵，纪名刚.机械设计［M］.北京：高等教育出版社，2001.

［3］ Barlam D,Zahavi E.The reliability of solutions in contact problem s ［J］.Comp&Struct,1999,70:35－45.

［4］ 苏春峰，艾延廷，娄小宝.接触非线性仿真中接触刚度因子选取的方法研究 ［J］.沈阳航空工业学院学报，2009（6）：5－9.

［5］ 尹长城.不同加载方式的斜齿轮接触分析 ［J］.湖北汽车工业学院学报， 2011， 25（2）：28－31+42.

［6］张建辉，严运兵，马迅.基于ANSYS Workbench及APDL的鼓式制动蹄有限元分析［J］.湖北汽车工业学院学报， 2011， 25（3）:13－17.