一道高考题的解答及一般式研究

●

(玉门市第一中学 甘肃玉门 735211)

一道高考题的解答及一般式研究

●谢鹏作

(玉门市第一中学 甘肃玉门 735211)

2011年山东省数学高考理科试题第15题新颖别致、富有创意,令人赏心悦目、回味无穷.在追寻命题目的,领略考题智慧,挖掘深刻内涵之时对其一般式进行研究,下面给出2种解法及一般式的求解,以供读者参考.

1 题目

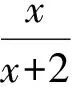
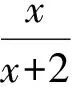
根据以上事实，由归纳推理可得:当n∈N*且n≥2时，fn(x)=f(fn-1(x))=________.

本题的命题意图是考查学生观察、分析、归纳推理及猜想能力,要求学生根据题目的结构特征,从众多的信息中提取、挖掘出有效的数据信息,并加以整理,找出规律.

2 题目的解答

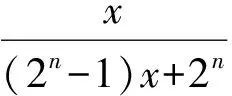
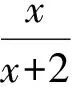
(2)假设当n=k时,

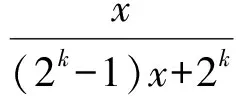
成立.那么当n=k+1时,

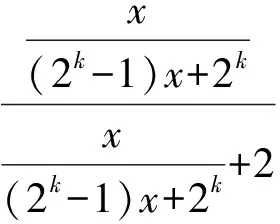
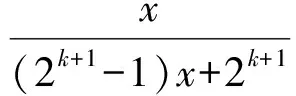
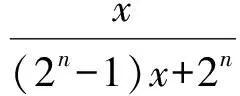
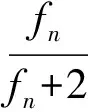
x1=0,x2=-1,

因此

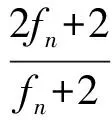
即

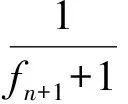
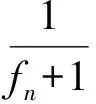
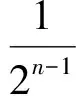
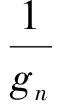
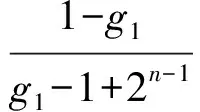
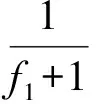
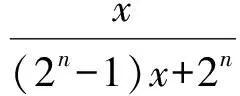
3 推广

下面,对函数一般式fn(x)进行研究.

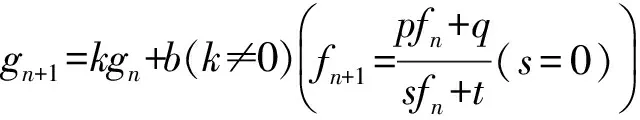
因为gn+1=kgn+b(k≠0),所以

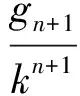
由累加法可得

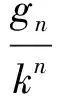
因此gn=g1kn-1+b(1+k+k2+…+kn-2).

当k=1时,gn=g1+(n-1)b;

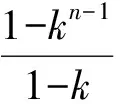
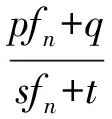
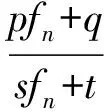
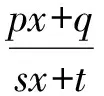
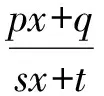
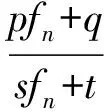
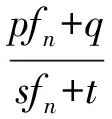
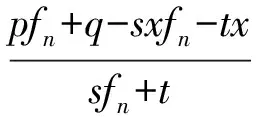
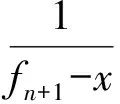
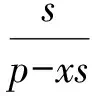
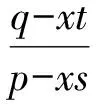
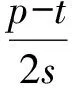
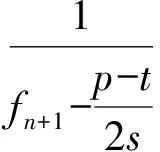
即

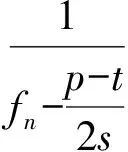
由此可解得fn.

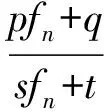
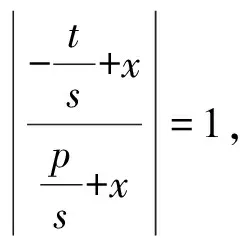
高考试题研究是教学的一项重要而常规的工作.它不仅引领、导向课堂教学,而且把握高考试题的发展方向;不仅研究知识之间的联系,解答方法的多样性与灵活性,更要研究试题的推广、拓展及一般式.只有这样,才能更深入地理解试题,发挥它在教学中的地位,提高教学质量.