基于线性变换的多项式模型*

尹 智 王解先 许才军

(1)武汉大学测绘学院，武汉 430079 2)同济大学测量与国土信息工程系，上海200092)

基于线性变换的多项式模型*

尹 智1)王解先2)许才军1)

(1)武汉大学测绘学院，武汉 430079 2)同济大学测量与国土信息工程系，上海200092)

通过比较基于线性变换的多项式模型和传统纯量多项式模型的项数、模型参数、模型运算性质以及模型所能表示对象的集合，并进行算例分析发现，基于线性变换的多项式模型形式更加简洁，模型参数具有直观的几何意义和良好的运算性质，更适合表达多维高次对象，在工业测量领域的应用中更容易确定必要的拟合参数，整体上更具有优越性。

线性变换;多项式模型;纯量多项式模型;仿射对象;正射对象

1 引言

传统的纯量多项式模型是用完全展开的多项式方程来表示数学对象的模型，它可以应用于各学科［1-3］。

虽然这种模型方便易用，但在很多情况下仍有诸多不便，比如在描述多维高次对象时，由于纯量多项式模型的项数非常多而影响运算的简便性，这时人们通常就会舍去大量的复杂项而保留一些简单项进行研究，致使模型本身失去完整性。另外，在描述多维高次对象时，纯量多项式模型的各个参数之间通常具有相关性，没有直观的意义，尤其在工业测量领域难以确定模型必要的拟合参数，这也是人们不常使用复杂的多维高次纯量多项式模型的原因。

鉴于纯量多项式模型的不足，本文将推导基于线性变换的多项式模型，并分析和研究该模型的各种性质。

2 多项式模型的分类和线性变换

多项式模型的分类方法有多种，根据解析式形式，可总结为多项式元数分类法、多项式次数分类法和特征根符号分类法。

多项式元数分类法和多项式次数分类法分别是根据多项式中出现的元数和各元的最高次数对多项式模型进行分类的方法。

多项式特征根符号分类法根据多项式的特征根符号的组合方式对多项式模型进行分类。此方法建立在前两种分类方法基础上，即多项式模型经过元数分类和次数分类以后，利用特征根符号的组合方式进一步分类。文献［4］在拟合三元二次曲面(空间二次曲面)时采用以特征根为参数的拟合方法，在拟合时特征根的可能出现形式有3种：零特征根、正特征根和负特征根。笔者认为，可以根据这些特征根符号的组合方式对多项式模型分类。比如，在不含交叉项的多项式模型中，x2-y2=2和-x2+ 4y2=1的特征值(x2项的符号和y2项的符号)都是一正一负，属于同一类多项式模型对象。

由3种分类方法可知，圆和椭圆都是二元二次曲线，且它们的特征根符号组合方式也相同，所以可以将圆和椭圆归于同一类对象。以下将从线性变换的角度研究单位圆至任意椭圆或圆的线性变换过程。

通常，基本的线性变换形式有：伸缩变换、旋转变换和平移变换。单位圆可以通过线性变换得到任意椭圆或圆，变换的各个阶段见图1至图4，不同阶段的横轴和纵轴采用不同的字母表示，坐标分别记为U=(u v)T、X'=(x'y')T、X″=(x″y″)T和X =(x y)T。

图1中，单位圆的解析式为

式(1)也可表示为

1)轴向伸缩变换

将图1中的圆在u轴方向收缩l1倍，在v轴方向收缩l2倍，变为图2中的椭圆，该变换相当于用l1X'替换式(2)中第一项的U，用l2X'替换式(2)中第二项的U，多项式模型的解析式变为

2)旋转变换

将图2中的椭圆长轴和短轴分别以原点为中心做旋转变换，以逆时针旋转方向为正，旋转角度分别为α1和α2。如果α1≠α2，得到原图形的仿射图形;如果α1=α2，得到原图形的正射图形。在本例中，令α1=α2，变为图3中的椭圆，该变换相当于用R1X″和R2X″分别替换式(3)中第一项的X'和第二项中的X'，多项式模型的解析式变为

式中：

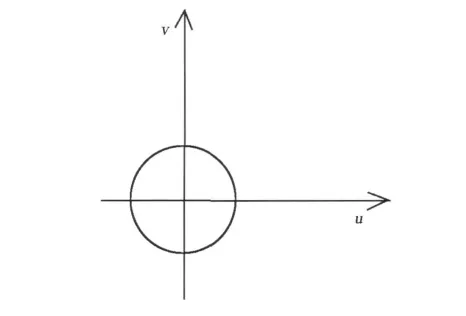
图1 标准图形(单位圆)Fig.1 Standard shape(unit circle)

图2 伸缩变换后的图形(椭圆)Fig.2 Shape after stretching and drawing(ellipsoid)

3)平移变换

将图3中的椭圆以椭圆中心为基点平移至新的位置，平移向量为X0=(x0y0)T，变为图4中的椭圆，该变换相当于用X-X0替换式(4)中的X″，多项式模型的解析式变为

至此，式(5)便可以表示平面里的任意一个椭圆或圆。

图4 平移变换后的图形(椭圆)Fig.4 Shape after translation(ellipsoid)

3 基于线性变换的多项式模型

设多项式模型的元数为n;多项式模型的次数向量为k=(k1，k2，…，ki，…，kn)，ki是第i项的次数，max(ki)决定多项式模型的次数;多项式的符号向量为δ=(δ1，δ2，…，δi，…，δn)，δi是第i项的符号，可以取值+1、-1或者0。与上述推导类似，其他类的对象也存在各自类的标准对象和一般对象。其中，标准对象的多项式模型为

式(6)展开后可以写为：

标准对象经过轴向伸缩变换、旋转变换和平移变换可以得到该类对象的一般对象，即可得到本文介绍的基于线性变换的多项式模型：

参数n、k和δ决定多项式模型的类别，可称之为分类参数;参数l、A和X0决定多项式模型的线性变换过程，可称之为变换参数。

4 模型分析

4.1 模型项数的比较

纯量多项式模型在表示较少元数和较低次数的对象时使用非常方便，但是随着表达对象的元数和次数增长，其项数的增加速度非常快。如表1，对于三元三次多项式模型，基于线性变换的多项式模型只有4项，而纯量多项式模型已经达到20项。限于篇幅，本文没有列出更多的多维高次多项式模型的实例，但可以验证，随着多项式模型的次数和元数的增加，纯量多项式模型的项数增加速度迅速，这在实际应用中造成了极大的不便。

基于线性变换的多项式模型中，每一项均包含矩阵，其项数始终只比模型的元数多一项，模型解析式十分简洁，使用该模型表达多维高次的对象时仍然非常方便。

4.2 模型参数和运算性质的比较

以表1中二元二次多项式对象为例，其纯量多项式模型为：

表1 两种多项式模型解析式的项数比较Tab.1 Comparison between the number of polynomial model items of the two model

相应地，其基于线性变换的多项式模型为：

通过纯量多项式模型难以辨别该对象的几何性质;然而，通过基于线性变换的多项式模型，则容易根据各个参数的数值和符号辨别该对象的几何性质。比如，由式(10)可以判断，该对象是由标准双曲线x2-y2=1在x轴向伸长2倍，在y轴向伸长3倍，逆时针旋转π/6，x轴正向平移1个单位，y轴正向平移2个单位后形成的双曲线。

分析说明，基于线性变换的多项式模型参数具有明显的几何意义且互不相关。

另外，在工业测量拟合领域中，需要对多项式模型的参数求导并做相应计算［4］，所以多项式模型运算性质的方便与否对于模型的实际使用影响很大。

设椭圆的基于线性变换的多项式模型为：

对各个参数分别求导，结果为：

可见，基于线性变换的多项式模型求导运算较为方便，其参数具有明显的几何意义且互不相关，对参数求导也较为方便，因此，该模型比纯量多项式模型更适合应用于拟合大型几何形体的工业测量领域。

4.3 模型表示对象集合的比较

本文模型既能表达正射图形，也能表达仿射图形。如图5，图形Ⅰ(圆)是基于线性变换的多项式模型，解析式为(11)，图形Ⅱ(椭圆)是基于线性变换的多项式模型解析式为(12)。其中，椭圆是圆的仿射图形。

图5 用基于线性变换多项式表达正射对象和仿射对象(单位：m)Fig.5 Ortho object and affine object expressed by polynomial model based on linear transformation(unit：m)

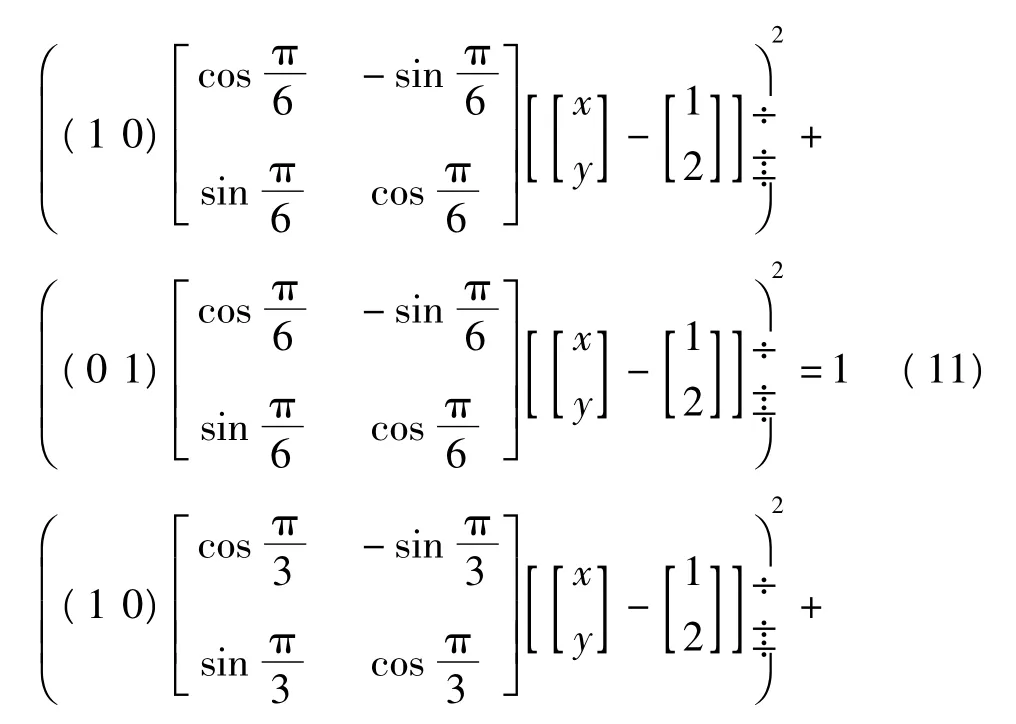
式(11)中x轴和y轴的旋转角都为π/6;式(12)中x轴的旋转角为π/3，y轴的旋转角为π/6。该例说明，如果两个平面坐标轴的旋转变换角不同，则表达的是仿射对象，否则是正射对象。

同理，在基于线性变换的多项式模型(8)中，Ri是对第i个轴进行旋转变换的矩阵。如果线性变换过程中各个坐标轴旋转的角度不同，则模型表达的是仿射对象;否则，表达的是正射对象。这说明基于线性变换的多项式模型与纯量多项式模型表达的对象集合一致，都可以表达仿射对象，若对模型进行一定条件的约束则可以表达正射对象。

另外，如果将基于线性变换的多项式模型中的矩阵展开，则基于线性变换的多项式模型解析式可以转换为纯量多项式模型的解析式。矩阵展开的过程是可逆的，这也说明基于线性变换的多项式模型和纯量多项式模型的等价性，两者表示的对象集合相同。

5 算例

采用基于线性变换的多项式模型对文献［4］中圆的模拟观测数据分别进行拟合，与原文献的拟合效果进行比较，分析多项式模型在工业测量拟合中的应用价值。

拟合流程图如图6所示，两种模型拟合得到的结果如表2所示。

图6 两种模型的拟合流程图Fig.6 Flowchart of simulation by the two models

表2 模拟观测值和拟合结果比较(单位：dm)Tab.2 Simulated observed values and comparison between the fitting results(unit：dm)

比较结果可以看出，两种模型的拟合结果一致。然而，基于线性变换多项式模型在确定必要参数方面更加方便。如图6，在拟合流程的第②步，对于纯量多项式模型，需要解析几何的相关理论来辅助判断参数之间的相关性，进而确定必要参数，整个过程可能需要大量的公式推导，尤其对于少见的高次几何形体，解析推导过程更加复杂;对于基于线性变换的多项式模型，则可以方便地根据拟合目标对象的先验信息固定模型中的一些参数，从而高效地消除参数之间的相关性，获得必要的参数和化简多项式模型。本文采用简单的二维平面图形(圆)来说明该模型确定必要参数的方便性，若推广到三维高次几何形体的拟合情况，该优点更加明显。

6 结论

1)基于线性变换的多项式模型的参数具有明显的几何意义且互相独立，对参数求导方便，在参数性质和运算性质方面优于纯量多项式模型;

2)表示多维高次对象时，该模型的项数相比纯量多项式模型少很多，书写形式更加简洁;

3)基于线性变换的多项式模型所能表示的对象集合与纯量多项式模型的保持一致;

4)应用于工业测量拟合时，基于线性变换的多项式模型更容易通过拟合目标对象的先验信息(如几何对称性)确定拟合的必要参数。

1 王解先.工业测量中一种二次曲面的拟合方法［J］.武汉大学学报(信息科学版)，2007，32(1)：47-50.(Wang Jiexian.A method for fitting of conicoid in industrial measurement［J］.Geomatics and Information Science of Wuhan U-niversity，2007，32(1)：47-50)

2 张震宇.基于成像模型的星载SAR影像几何纠正［D］.同济大学，2009.(Zhang Zhenyu.Geometric rectification of satellite SAR image based on imaging model［D］.Tongji University，2009)

3 许伟志.二元散乱数据多项式自然样条拟合及其应用［D］.中山大学，2010.(Xu Weizhi.Bivariate polynomial nature splines fitting for scattered data and its applications［D］.Sun Yat-Sen University，2010)

4 王解先，季凯敏.工业测量拟合［M］.北京：测绘出版社，2007.(Wang Jiexian and Ji Kaimin.Industrial surveying fitting［M］.Beijing：Surveying and Mapping Press，2007)

5 朱雷鸣，等.直角坐标系的欧拉旋转变换及动力学方程［J］.海洋测绘，2010，30(3)：20-22.(Zhu Leiming，et al.The Euler’s rotation and dynamic equation of rectangular coordinate system［J］.Hydrographic Surveying and Charting，2010，30(3)：20-22)

POLYNOMIAL MODEL BASED ON LINEAR TRANSFORMATION

Yin Zhi1)，Wang Jiexian2)and Xu Caijun1)

(1)School of Geodesy and Geomatics，Wuhan University，Wuhan 430079 2)Department of Surveying and Geo-informatics，Tongji University，Shanghai200092)

After summarizing the classification methods of polynomial model，the linear transformation from a unit circle to any ellipse or circle is studied，thus the polynomial model based on linear transformation is derived.By comparing the polynomial model based on linear transformation with the traditional scalar polynomial model on the number of items，the model parameters，calculation properties and the collection of objects that can be represented by model，as well as giving an analytical example about the plane circle fitting，it is found that the new model has a more compact form，its parameters have perceptual geometric meaning and good operational properties，it is more suitable for the expression of the higher-dimensional and higher-degree polynomial object.Particularly it is more convenient to obtain the necessary parameters in industrial surveying field.On the whole，the polynomial model based on linear transformation has more advantages.

linear transformation;polynomial model;scalar polynomial model;ortho object;affine object

1671-5942(2011)05-0091-06

2011-03-01

国家自然科学基金(40874003)

尹智：男，硕士研究生，主要研究方向为大地测量与测量工程.E-mail：yinzhi1221@sina.com.cn

P207

A