基于加权总体最小二乘法的GPS高程拟合*
赵 辉 张书毕 张秋昭
(1)中国矿业大学环境与测绘学院,徐州 221008 2)国土环境与灾害监测国家测绘局重点实验室,徐州221008)
基于加权总体最小二乘法的GPS高程拟合*
赵 辉1,2)张书毕1)张秋昭1,2)
(1)中国矿业大学环境与测绘学院,徐州 221008 2)国土环境与灾害监测国家测绘局重点实验室,徐州221008)
在GPS高程拟合中,针对传统最小二乘方法不能解决系数矩阵存在误差的问题,提出了一种基于加权总体最小二乘的拟合方法。对平面和二次曲面多项式建立更加合理的拟合模型,并给出了相应的迭代算法。实例计算表明,加权最小二乘方法能够得到更好的估计参数,高程异常值拟合精度也相应提高。
GPS高程;多项式拟合;EIV模型;最小二乘;加权总体最小二乘
1 引言
在实际工程应用中,我国高程系统普遍采用正常高。传统水准测量获取基于似大地水准面的正常高,而GPS定位技术,也可以得到基于WGS84参考椭球的大地高,且操作简单方便[1]。用GPS定位技术获取的正常高去满足工程应用需要,需进行高程系统的转换,也就必须要知道测点的高程异常值。
对于大多数工程应用,由于测区范围不大,高程异常变化平缓,多项式拟合便可满足精度要求[2]。该方法的基本原理是将高程异常值与平面坐标近似描述为多项式关系,利用同时已知大地高和正常高的公共点组成误差方程,根据最小二乘原理求解多项式系数。然而采用经典的Gauss-Markov模型,并不能解决在系数矩阵中含有误差的问题。如果观测向量和系数阵都存在误差,那么最小二乘解将不再最优,而是有偏的[3]。为此,本文引入基于加权总体最小二乘(WTLS)的GPS高程多项式拟合,并利用实例数据对算法可行性进行验证。
2 总体最小二乘
2.1 EIV函数模型
观测变量含有误差的EIV(Errors-In-Variable)线性函数关系式为[4,5]

其中,y为含有随机误差ey的n维观测向量,A为含有随机误差EA的n×m维系数矩阵,x为m维待估参数向量。随机误差具有如下统计性质:
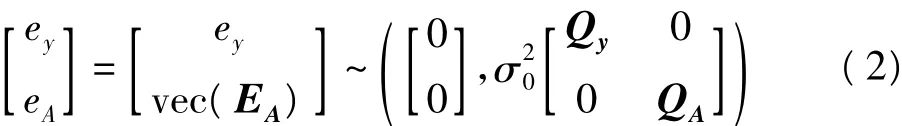
式中,vec表示矩阵列向量化算子,协因数阵Qy=,QA=。在总体最小二乘准则下,可解得顾及系数阵误差的参数估计

对于多元同方差的EIV模型,观测值权阵Py和系数矩阵权阵PA均为单位阵,可采用迭代法解算参数估值[6,7]:


2.2 加权总体最小二乘
对于广义总体最小二乘(GTLS)中的系数阵权阵,按

通过迭代可求解参数的WTLS估计,并进行精度评定。迭代步骤如下[8,9]:
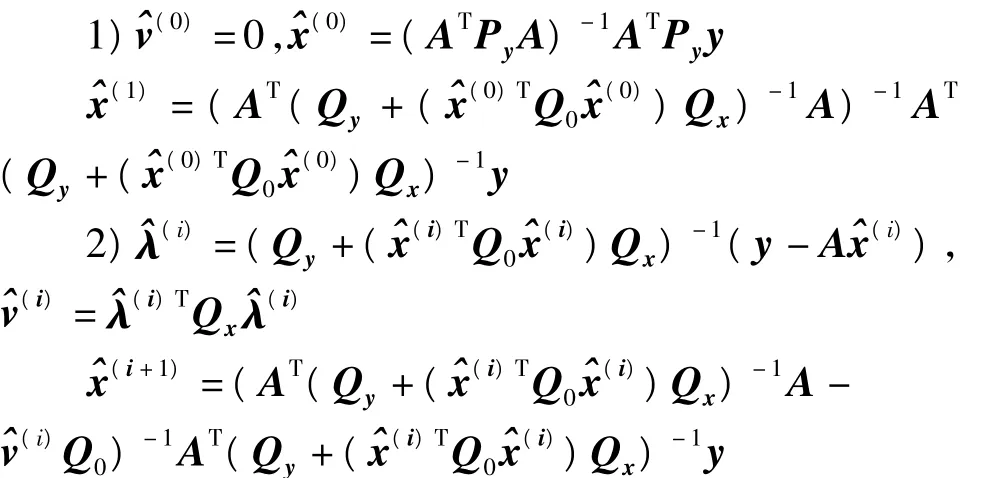
3 考虑系数阵误差的多项式高程拟合
GPS高程拟合多用平面和二次曲面多项式,考虑到由于系数阵存在误差,本文引入基于加权总体最小二乘的解算方法。
二次曲面多项式拟合函数模型为:

式中,ζi为平面坐标(xi,yi)点的高程异常,ai(i=0,…,5)为多项式待估参数。可写成形如式(1)的矩阵形式,式中

设平面坐标和高程异常值具有同等精度,σx= σy=σζ。对于平面多项式,只需取系数阵A的前3列。由于第一列为常数,从而可令P0第一列为零,则
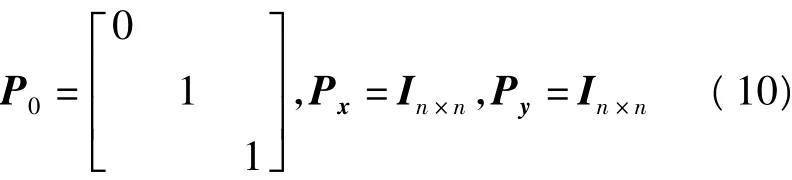

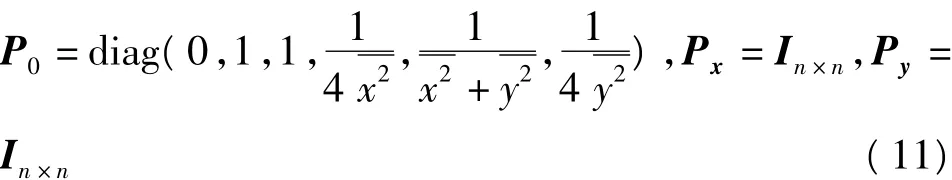
4 实例分析
采用某市20个GPS联测水准的高程数据,分析总体最小二乘对多项式GPS高程拟合的可行性与有效性,取均匀分布的前10个点为拟合公共点,其余10个点为外部检核点。点位分布如图1所示。
为保证计算精度,先对坐标数据进行标准化处理,组成观测方程。分别采用传统最小二乘、总体最小二乘和加权最小二乘求得平面和曲面多项式的拟合参数,表1和表2中列出了3种方法的参数估值与单位权中误差。
由表1和表2可以看出,3种方法对平面拟合和二次曲面拟合参数求解,采用传统最小二乘和总体最小二乘两者计算结果并无太大差别。然而加权总体最小二乘单位权中误差都有所提高,参数估值的精度更好。
图2为加权总体最小二乘平面和二次多项式拟合残差,从图2可以看出最大残差为6 cm,大多数在2 cm附近。图3为传统最小二乘与总体最小二乘、加权总体最小二乘拟合残差的较差,可以看出总体最小二乘法对残差提高不大,而加权总体最小二乘法可提高2 mm左右。

表1 平面拟合参数结果及精度(单位:m)Tab.1 Plane fitting results and their accuracy with some method(unit:m)

图1 GPS水准点位分布Fig.1 Distribution of GPS leveling points

图2 WTLS拟合残差Fig.2 Residuals of fitting with WTLS

图3 LS与TLS、WTLS拟合结果较差Fig.3 Comparison among the fitting results with LS、TLS and WTLS

表2 二次曲面拟合参数结果及其精度(单位:m)Tab.2 Quadric surface fitting results and accuracy with three methods(unit:m)
5 结语
传统最小二乘方法在系数阵存在误差的情况下,并不能很好地估计多项式系数参数。考虑到估计系数阵含有误差和观测变量不等精度,采用了更加合理的加权总体最小二乘方法。根据实例计算结果,加权总体最小二乘方法的单位权中误差更小,检核点残差也相应减小。在GPS高程拟合中,加权总体最小二乘法可以提高精度。
1 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2010.(Li Zhenghang and Huang Jinsong.GPS surveying and data processing[M].Wuhan:Wuhan University Press,2010)
2 徐绍铨,等.GPS测量原理及应用[M].武汉:武汉大学出版社,2008.(Xu shaoshuai,et al.The principle and application of GPS surveying[M].Wuhan:Wuhan University Press,2008)
3 邱卫宁,等.测量数据处理理论与方法[M].武汉:武汉大学出版社,2008. (Qiu Weining,et al.The theory and method of surveying data processing[M].Wuhan:Wuhan University Press, 2008)
4 Chi Lun Cheng,Mastrondrdl N and Palge C.Total least squares and errors-in-variables modeling[J].Computational Statistics and Data Analysis,2007,52:1 076-1 079.
5 王乐洋,许才军,鲁铁定.病态总体最小二乘模型的正则化算法[J].武汉大学学报(信息科学版),2010,35(11):1 346-1 350.(Wang Leyang,Xu Caijun and Lu Tieding.Ridge estimation method in Ill-posed weighted total least squares adjustment[J],Geomatices and Information Science of Wuhan University,2010,35(11):1 346-1 350)
6 Burkhard Schaffrin.A note on constrained total least-squares estimation[J].Linear Algebra and its Applications,2006,417:245-258.
7 Schaffrin B and Felus Y A.On the multivariate total leastsquares approach to empirical coordinate transformations.three algorithms[J].Journal of Geodesy,2008,82(6):373-383.
8 Schaffrin B and Wieser A.On weighted total least-square adjustment for linear regression[J].Journal of Geodesy,2008,82:415-421.
9 陈玮娴,等.加权总体最小二乘在三维激光标靶拟合中的应用[J].大地测量与地球动力学,2010,(5):90-96.(Chen Weixian,et al.Application of weighted total leastsquares to target fitting of three-dimensional laser scanning[J].Journal of Geodesy and Geodynamics,2010,(5):90 -96)
GPS HEIGHT FITTING OF WEIGHTED TOTAL LEAST-SQUARES ADJUSTMENT
Zhao Hui1,2),Zhang Shubi1)and Zhang Qiuzhao1,2)
1)School of Environment and Spatial Informatics,China University of Mining and Technology,Xuzhou 221008 2)Key Laboratory for Land Environment and Disaster Monitoring of SBSM,Xuzhou 221008
In GPS height fitting,a new method of Weighted Total Least-Squares adjustment(WTLS)is presented for solving the error of coefficient matrix.A more reasonable fitting model of plane and quadric polynomial is established,and the corresponding iterative algorithm is given.The examples of calculations show that the polynomial parameter is more reasonable and the solved height anomaly is more accurate.
GPS height;polynomial fitting;errors-in-variables model;least square;weighted total least-square
1671-5942(2011)05-0088-04
2011-03-14
江苏省普通高校研究生科研创新计划项目(CXLX11-0323)
赵辉,男,1987年生,硕士,研究方向:GNSS理论及应用研究.E-mail:zhaohui@cumt.edu.cn
P207
A

