DEA及其在上市公司融资效率分析中的应用研究

鲍金良 胡伟

DEA及其在上市公司融资效率分析中的应用研究

鲍金良 胡伟

近些年来，数据包络分析被用来评估很多不同种类实体效益的应用。其中一个非常重要的原因就是，因为经常有很多未知的复杂的因素，使得输入活动和输出活动存在很多种联系。但是数据包络分析却不需要考虑这些联系，因此它为解决这些情况提供了可能。本文简略介绍了DEA分析方法中的两个常用模型，并且以创业板在2011年1月份上市的15家公司为例，对其进行了DEA效率分析。

DEA；常用模型；融资效率

一、DEA方法简介

数据包络分析（Data Envelopment Analysis，DEA），是一种测度效率的非参数方法。它是基于法雷尔的前沿生产函数思想，能够评价具有相同类型的投入产出的若干决策单元（DecisionMakingUnits，DMU）的相对效率。由于任何一个生产过程都可以看成是一个生产单元在其可能的范围内，通过一定生产要素的投入，而得到一定数量的产出的活动。而且活动的目的都是尽可能的以最小的投入，达到最大的产出。由于从生产要素的投入到最后的产出之间，都需要经过一系列决策才能实现。这种需要决策的单元被称为决策单元（DMU）。同类型的DMU是指具有如下特征的DMU集合：第一，它们具有相同的目标和任务；第二，它们具有相同的外部环境；第三，它们具有相同的输入、输出指标，且其值为非负。

假设某DMU在一项经济活动中的输入指标为x=（x1，x2，…，xm）τ，输出指标为y=（y1，y2，…，ym）τ。定义T={（x，y）｜输入指标x能生产输出指标y}为所有可能的生产活动所构成的所有生产可能集。而由（xj，yj）（j=1，2，…，n）组成的集合T={（x1，y1），（x2，y2），…，（xn，yn）}为参考集。

为了研究方便，我们假设所有生产可能集均满足下列四条公理：

（1）凸性：对于任意的（x，y）∈T和（x′，y）∈T，μ∈[0，1]则有

μ（x，y）+（1-μ）（x′，y）∈T

即如果用输入指标x，x′分别和μ，（1-μ）相乘后的和作为新的输入指标，那么可以得到和原来产出相同倍数的和的新产出。

（2）锥性：若（x，y）∈T及k≥0，则有

K（x，y）=（kx，ky）∈T

即如果用原输入的k倍作为新的输入，则能够得到原产出的k倍。

（3）无效性：设（x，y）∈T，若x′≥x，则（x′，y）∈T；若y′≤y，则（y，y′）∈T。即在原来生产活动的基础上，增加投入或减少产出是可行的。

（4）最小性：生产可能集T是满足上述条件的所有集合的交集。

二、DEA方法的常用模型

目前，常用的DEA模型为C2R评价模型和C2GS2评价模型。C2R模型构建过程如下：设有n个决策单元，每个决策单元均有输入指标xj=（x1，x2，…，xm）τ，输出指标y=（y1，y2，…，ym）τ。对于任意决策单元DMU基于凸性、锥型、无效性和最小性公理假设，有生产可能集：

可以得到DEA的C2R 模型：

其中，m、s分别表示输入指标、输出指标的个数；xijo、yrjo分别表示第jo个DMU的第i项输入和第r项输出；s、s表示松弛变量；ε为非阿基米德无穷小量，在计算中为正值的无穷小。

C2GS2模型构建如下对DMU仅基于凸性、锥型和无效性个公理假设，有生产可能集：

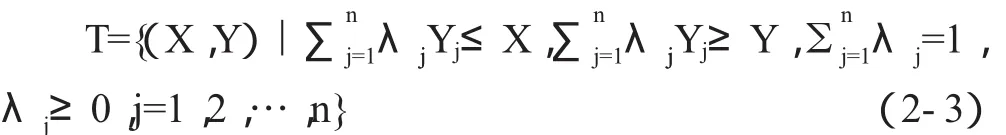
可以得到以下模型：

其中各符号意义表示同上。

三、评价模型的经济解释

通过上述部分构建的DEA模型，将目标DMU的投入产出指标代入，计算出对应的DMU的融资效率值。

在模型（2-2）中，当最优解为：

（1）θ*=1，s=0，s=0，则称决策单元j0为DEA有效（C2R），即决策单元j0在原投入X0基础上能够得到的产出Y0已经达到最优。其中系数θ可以理解为决策单元DMUj0投入向量的“压缩系数”，是DEA的相对效率值。

如果θ*=1，s=0，=0，该决策单元同时为规模报酬不变和技术效率最佳。也就是说不仅仅投入不可能等比减少，同时也不存在“过量”投入和“亏量”产出，该决策单元处于有效状态，即DEA有效（C2R）。

（2）θ*=1，s≠0，或≠0，则称决策单元j0为DEA弱有效（C2R），即决策单元j0的部分投入Xi0可以减少s-*而保持原产出Y0不变，或者在保持原投入X0不变的情况下，使得部分产出Yj0提高s+*。

如果θ*=1，但是s，s不全为零，则表明非同时规模报酬不变和技术效率最佳。虽然投入已经不用等比减少，但是投入和产出上仍然有不足之处，某些方面仍存在“过量”投入或者“亏量”产出。没有达到最佳，因此为DEA弱有效（C2R）。

（3）θ*＜1，且s≠0，s≠0，则称决策单元j0为DEA无效（C2R），即决策单元j0的投入不当，可以通过将原投入X0按θ等比例减少，而使原产出Y0保持不变。

如果0＜θ*＜1，则表明该决策单元的投入不当，可以做全方面的等比减少，也就是说该决策单元非DEA有效（C2R）。

在模型（2-4）中，当最优解为：

（1）θ*=1，0，=0，则称决策单元j0为DEA有效（C2GS2），即决策单元j0在原投入X0的基础上，获得的产出Y0已达最优。即表明该决策单元技术效率最佳。

（2）θ*＜1，或s≠0，s≠0，则称决策单元j0为DEA无效（C2GS2）。若s≠0，表明存在“超量”投入；若s≠0，表明存在“亏量”产出；若0＜θ*＜1，表明该决策单元投入不当，可以做全面的等比减少，这些均属于非技术有效。

在现有的DEA模型中，如果仅就有效性而言的话，C2R模型可以用来评价决策单元是否同时为规模有效和技术有效的总体有效，而C2GS2模型仅仅只评价技术效率是否为最佳，把这两者结合起来，便可以对决策单元规模效率和技术效率做出综合的评价。

四、DEA方法在上市公司融资效率分析中的应用

本文以2011年1月份在创业板上市的15家上市公司为样本，通过DEA方法来测量它们的融资效率。要用DEA方法来测量融资效率的时候，首先需要确定DMU的输入输出指标。本文将主营业务成本和资产负债率作为输入指标，将主营业务收入和净资产收益率作为输出指标。指标的数据的均来源于各上市公司经过审计的招股说明书，且均为截止2010年6月30日时的半年财务数据。具体如表1所示。

目前，DEA分析软件有很多，例如：DEA-SOLVER，DEA-FRONTIER，WINQB等。本文使用DEA分析软件为DEA-SOLVER_Pro5来进行数据分析处理。在分析指标之前，需要对各指标进行无量纲化。本文使用功效系数法。功效系数法下的无量纲化函数关系如下：

设max1sisn=Zij=aj（aj为第j项指标的最大值），min1sisnZij=bi（bi为第j项指标的最小值），则Zij∈[0.1，1.1]。

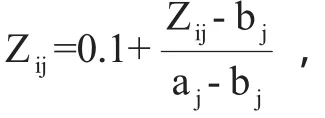
处理后的数据如表2所示。

使用DEA-SOLVER_Pro5来处理上表经过无量纲化后的数据，处理后的得到表3。

根据Michael Norman与BarryStocker对DEA效率值的研究，将DEA效率值分为4类，即：强势效率单位（The RobustlyEfficient Units），相对效率值为1，松弛变量全部为0；边缘效率单位（The Marginal Efficient Units），相对效率值为1，松弛变量不全部为0；边缘非效率单位（The Marginal Inefficient Units），单位整体效率值介于1与0.9之间，表示只要在投入产出项稍作调整即可达到效率值为1的水准；明显非效率单位（The DistinctlyInefficient U-nits），单位整体效率值低于0.9，表示该单位经营效率不佳。

那么就可以看出2011年1月份上市的15家公司中，只有2家为强势效率单位，其余均为明显非效率单位。即这15家上市公司的整体融资效率并不高。

五、DEA的分析总结

通过DEA在上市公司融资效率的分析中，我们可以看出DEA分析有着以下的优点：（1）它和传统的评价方法不一样，DEA方法可以同时对不同决策单元在不同时期内的产出水平进行综合评价。（2）DEA方法不需要通过主观确定各输入输出指标的权重，它只是将权重看作是变向量，在分析过程中通过某种原则进行确定。它使得通过DEA方法的出来的结论更加客观。（3）DEA方法在测量各决策单元的相对有效性的时候，注重的是对每个决策单元进行优化。因此，它得出来的相对效率是其最大值，所得出的权重也是最优的。（4）对于无效的决策单元，DEA方法不仅仅可以指出该决策单元的调整方向，并且还能够给出具体的调整量。（5）DEA方法的有效前沿面是一种内在生成的参照面，它是由有效决策单元所组成的，因此它更具有参照性和客观性。（6）DEA方法在测量决策单元的相对有效性的时候，它不需要估计该决策单元的生产函数，因此避免了由于采取了错误的生产函数，而得出了错误的结论的可能。

但是由于DEA方法其假设和自身方法的原因，同时也存在着如下几方面的局限性：（1）由于DEA模型的假设前提是在投入尽可能少的情况下，产出越大越好。但是在现实生产中，对于某些情况下的产出，并不是越大越好。例如，在工业生产中的废水、废渣、废气，这些产出并不是越大越好。（2）当在DEA分析中，对比投入产出指标的数量，如果DMU的数量并不足够大的时候，会显著影响DEA模型的辨析能力。为了提高DEA模型的评价功能，有学者认为投入产出指标的数量最好不要超过DMU总量的三分之一。（3）在DEA分析的结果中，只是简单的将DMU效率分为四个等级，即强势效率单位、边缘效率单位、边缘非效率单位和明显非效率单位。对于同为DEA有效的DMU来说，DEA模型认为它们一样的好。很显然这样的判断过于武断。（4）由于各个投入产出指标的权重是通过DEA模型计算出来的，而且在DEA模型中也没有对各个权重的取值范围加以任何限制。因此，在这种情况下，有可能出现对权重分配不切实际的问题。其带来的结果就有可能是：某项DMU有效，仅仅是因为其某项投入指标的权重过小，或者某项产出指标的权重过大。

[1]魏权龄.数据包络分析[M]，科学出版社，2004.

[2]卢福才.企业融资效率分析[D]，北京，中国社会科学院，2000.

[3]陈贤锦.基于DEA的上市公司股权融资效率分析[J],融资研究，2010，（4）.

[4]毛世平.技术效率理论及其测度方法[J]，农业技术经济，1998，（3）.

（作者单位：内蒙古财经学院）