CFD技术在无环量圆柱绕流多媒体教学中的应用研究

李国威 董金玲

辽宁工程技术大学 辽宁阜新 123000

CFD技术在无环量圆柱绕流多媒体教学中的应用研究

李国威 董金玲

辽宁工程技术大学 辽宁阜新 123000

CFD技术是当前高等院校多媒体教学的热门手段和方法，特别是在如流体力学这样概念抽象，理论性强，与实际流动现象结合紧密的课程中显得尤为突出。文章应用Gambit，Fluent和Tecplot等相关软件，对无环量圆柱绕流的流动机理进行数值模拟与分析。目的在于验证无环量圆柱绕流数学、物理理论的正确性，观察流动现象，分析产生各种现象的原因。通过研究表明，以直观演示和定量分析相结合的方法，能够非常好地解决许多教学中的难点和重点问题，使学生对抽象的教学内容产生深刻的印象，增强了学习兴趣。

CFD技术；多媒体；圆柱绕流；数值模拟；Fluent

流体力学课程是高等学校相关学科一门重要的技术基础课。该课程的特点是：知识容量大，概念与原理抽象、复杂，且与工程实际现象紧密结合，学生在学习该门专业课程时，普遍反映理论知识比较抽象，流体的运动规律难于想象与理解，且不能与具体流动现象相参照。同时，受教学条件的限制，任课教师很难形象地将流体动态流动的各种现象讲授给学生，这样使专业课的理论知识讲解与实际现象脱节。经过流体力学校级精品课程建设课题组多年的教学实践，将CFD技术引入流体力学课堂教学的教学方式，拓展了现有传统意义上的多媒体技术教学手段和方法。

笔者应用CFD技术的相关软件，对流体力学中的无环量圆柱绕流的流动机理进行数值模拟和仿真。验证无环量圆柱绕流数学、物理理论的正确性，动态地观察流动现象，分析产生各种现象的原因。研究结果表明：在流体力学多媒体教学中应用CFD技术，可以拓宽传统的教学方法和手段，为提高教学质量和收到良好的教学效果开辟了新的途径。

1 无环量圆柱绕流的基本理论

由于势函数和流函数满足的控制方程是线性的，因此它们的解具有可叠加性。依据这一原理，基本流动的复位势函数可以叠加起来给出较复杂的流动问题的解。其中无环量圆柱绕流就是沿轴方向均匀流与位于原点的源点在左汇点在右所组成负方向的偶极子叠加形成的(如图1所示)。

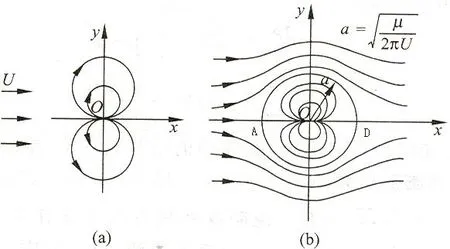
图1 均匀流与偶极子叠加

所形成流动的复势为：

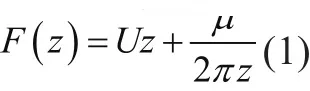
可求得复速度为：

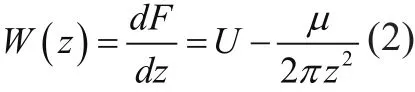
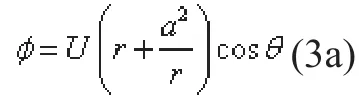
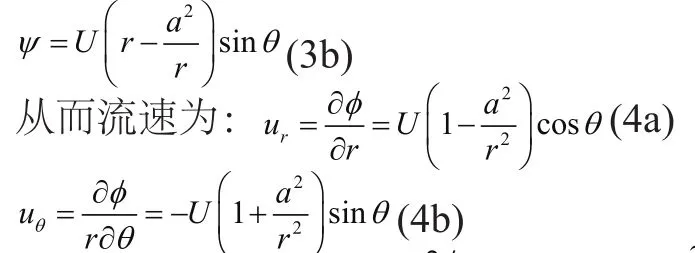
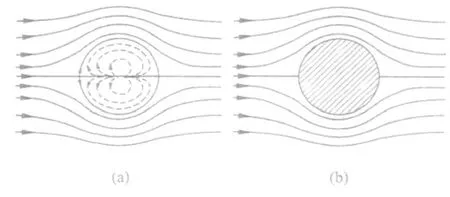
图2 圆柱绕流(无环量)

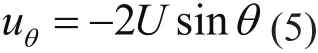
在θ=0，π处uθ=0，在柱面上ur=0，所以这两点为驻点，在θ=π2时uθ=−2U ，为切向最大速度的位置。对于恒定、无旋流动，伯努利方程为：

对于无穷远未受扰动流动，即p=p∞，uθ=U，代入(6)式得常数C=p∞+ρu22，从而可知流场中一点处的压强p ，即：

在柱面上ur=0，uθ=−2U sinθ，压强p为：

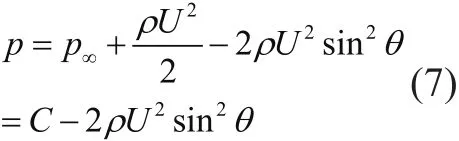
2 无环量圆柱绕流的数值模拟与讨论

使用仿真软件，首先明确研究对象性质，建立研究对象的物理模型，并建立研究对象数学模型；然后输入流体流动的初始条件和边界条件进行计算；最后输出所需的图像、曲线或数据等相关结果。本实例的已知模拟条件：模型长500mm，高300mm，圆柱直径10mm，均匀来流速度U=10m/s ，流动介质为水。通过模拟，得到结果如图3至图12所示：

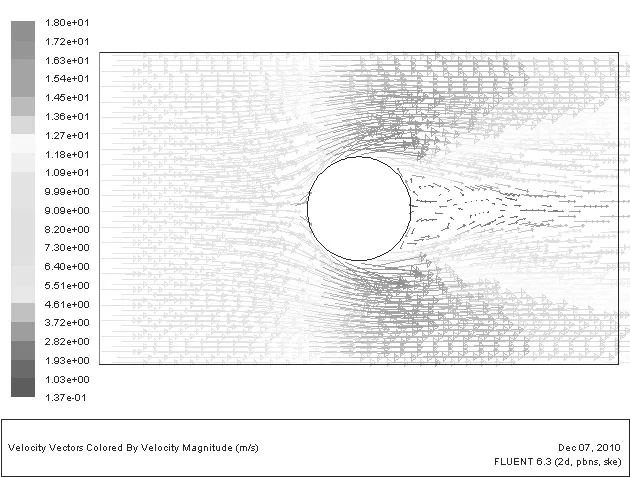
图3 圆柱绕流速度矢量图

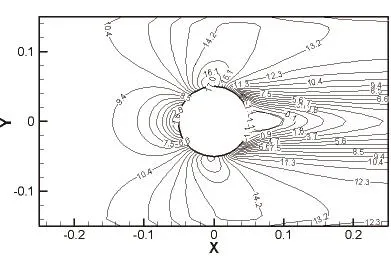
图4 圆柱绕流速度等值线图

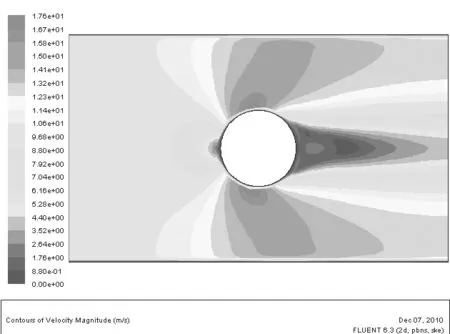
图5 圆柱绕流速度分布云图

图6 圆柱绕流绝对压强分布云图

图7 圆柱表面切应力矢量图

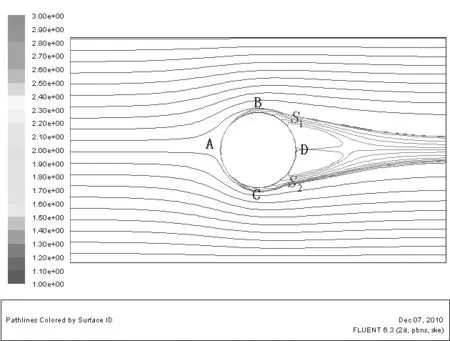
图8 流体圆柱绕流的流线

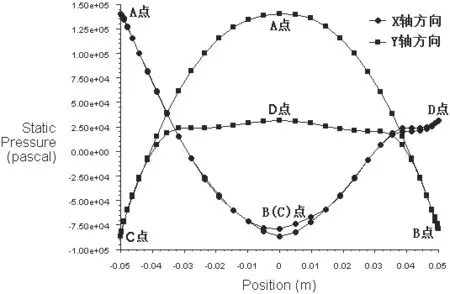
图9 圆柱表面流体的静压强分布曲线

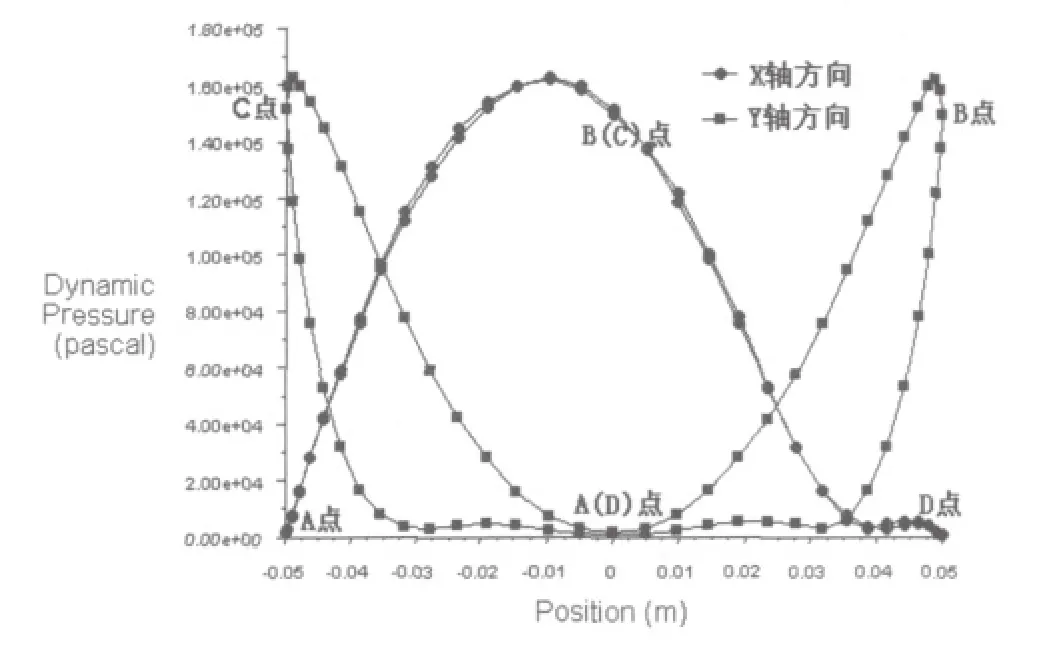
图10 圆柱表面流体的动压强分布曲线

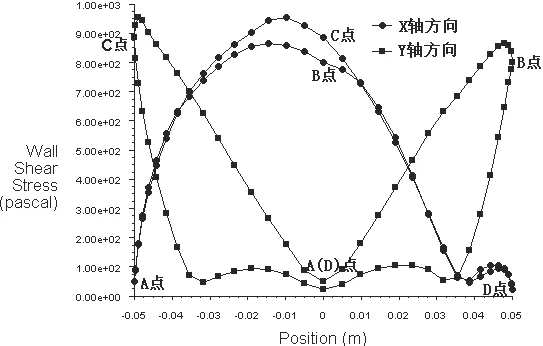
图11 圆柱表面流体的切应力分布曲线

图12 圆柱表面流体的速度分布曲线

对于理想流体的圆柱绕流,在圆柱上存在前驻点A和后驻点D,最大速度点B和,如图8所示。中心流线在前驻点分开,后驻点汇合。根据伯努利方程,流体质点绕过圆柱所经历的过程为在A−B()区,流体质点在A点流速为零，压强最大，以后质点的压强沿程减小，流速沿程增大，到达B点流速最大，压强最小。在B()−D区，流体质点的压强沿程增大，流速沿程减小，到达D点压强最大，流速为零。

对于粘性流体的圆柱绕流，图3、4、8、9和10说明，由于流体与固壁表面的粘附作用，在物面近区将产生边界层(如图8所示)。由于受到流体粘性阻滞作用，流体质点在由A点到B()点的流程中，将消耗部分动能用来克服摩擦阻力做功，以至使其无法满足由B()点到D点压力升高的要求，导致流体质点在B()−D流程内，流经一段距离就会将全部动能消耗殆尽(一部分转化为压能，一部分克服摩擦阻力做功)。于是，在壁面某点速度变为零，如图8中的，S2两点。以后流来的流体质点将从这里离开柱面进入下游主流场中，这一点称为分离点，这种现象称为边界层分离。在分离点之间的空腔内流体质点发生倒流，由下游高压区流向低压区，从而在圆柱后面形成了旋涡区。旋涡的产生使圆柱表面压强分布前后不对称，前驻点A的静压强要明显大于后驻点D的静压强，因此出现了流动阻力；而B,点的动压强明显大于A，D的动压强,如图9和10所示。图5、7、11说明，在理想情况下,流体流到B点和点时,速度达到最大值,切应力也达到最大值,但是由于实际流体产生粘性阻力,流体流到B点和点之前切应力就已经达到最大值,并且沿着流动方向是对称的。图12说明理想流体由于不考虑流体的粘性作用，因此圆柱表面的流体介质具有一定的速度,而实际流体由于存在边界层，因此圆柱表面的流体介质的速度为零。

3 结束语

(1)由于参数设置比较贴近实际，通过CFD技术得到的图像、曲线和动画，能够对实际的工程流动问题如无环量圆柱绕流，进行定性和定量分析。

(2)利用CFD技术能够逼真地、准确地模拟各种条件下实际流场的流动状态，有助于学生掌握和理解流动过程复杂或难以观察的，并且教师在语言上难以表达的各类流动现象。

(3)应用CFD商业计算软件制作出的图像、曲线和动画，经过后期处理，色彩绚丽多变，美观实用，使枯燥的课程变得富有生机和活力。通过教学实践表明，可以很好地调动学生学习的兴趣和热情，教学效果非常好。

[1] 李国威，崔俊奎.基于FLUENT的流体力学教学课件素材制作研究[J].中国现代教育装备，2009，5：76～77

[2] 郑捷庆，邹锋，张军，等.CFD软件在工程流体力学教学中的应用[J].中国现代教育装备，2007，10：119～121

[3] 董曾南，章梓雄.非粘性流体力学[M].北京：清华大学出版社，2003

[4] 董曾南，章梓雄.粘性流体力学[M].北京：清华大学出版社，1998

[5] Fluent Inc., FLUENT User′s Guide[Z].Fluent Inc.,2005

Application research of CFD technology in multimedia teaching of acyclic fl ow around cylinder

Li Guowei, Dong Jinling
Liaoning technical university, Fuxin, 123000, China

CFD technology is the popular tool and method in multimedia teaching of colleges and universities, especially in the course such as hydrodynamics which is of abstract concept, strong theoretical character, and is combined closely with practical fl uid fl ow. The article applies the soft wares such as Gambit, Fluent and Tecplot, etc. Simulates numerically and analyzes the mechanism of acyclic fl ow around cylinder. The aim is verifying the accuracy of mathematics theory and physical theory of the acyclic fl ow around cylinder, and observing the fl ow phenomena and analyzing the reason for generating the phenomena mentioned. The research shows that by combination of visible demonstration and quantitative analysis, most diffi culties and emphasis of teaching could be solved, and induces the students’ forms profound impression to abstract contents and enhances the learning interest of students.

CFD technology; multimedia; fl ow around cylinder; numerical simulation; Fluent

2010-12-07 稿件编号：1012038

李国威，在读博士研究生，讲师。

辽宁工程技术大学应用创新型人才培养立项课题“CFD技术在流体力学多媒体教学中的创新培养研究”(编号：YBQ104021)；辽宁工程技术大学“流体力学校级精品课程”(编号：2007-03)。