山地风场平均及脉动风速特性试验研究
孙 毅,李正良,黄汉杰,陈朝晖,魏奇科
(1.重庆大学土木工程学院,重庆 400045;2.中冶赛迪集团有限公司,重庆 400013;3.中国空气动力研究与发展中心,四川绵阳 621000)
0 引言
随着山地城市的现代化发展,大量高层和超高层建筑兴起,抗风设计工作需要较为准确的山地风场平均风速和湍流特性作为计算依据。
目前对于山地风场的研究集中在平均风速的加速效应(speed-up effect)上,即在山地地形中,某高度平均风速比平地相应高度平均风速有所增加的效应,一般在山顶的近地面最为明显。通常用一无量纲参数:加速比(speed-up ratio)来定量描述加速效应:

式(1)中U(z)表示山地地面以上z高度处的风速,U0(z)表示平地地面以上z高度处的风速。
国外从20世纪70年代开始,大量学者针对山地的加速效应进行了风洞试验和数值模拟研究。Jackson[1-2]和 Hunt[3]最先提出了一种计算二维光滑山体加速效应的解析算法,但这种算法仅仅适用于未发生流动分离的情况;Mason[4]将其算法延伸到单个三维山体的情况。Kaimal[5]通过研究指出,以 Jackson的方法为主体的算法,在计算未发生流动分离时的最大加速效应误差可以小于15%到18%。Taylor[6]提出了一种通过ΔSmax计算不同高度处ΔS的简便方法,称为“原始算法”(original Guidelines)。Gong[7]进行了二维山体和三维轴对称山体的风洞试验。Miller[8]在风洞中研究了连续12个二维山体的加速效应,并与一不规则地形的加速效应相比较讨论。Taylor[9]、Weng[10]先后运用边界层数值模拟研究了山体几何尺寸和地面粗糙度对加速比的影响,提出了可以考虑地面粗糙度影响的山顶加速比算法,称为“新算法”(new Guidelines)。Kim[11-12]指出加速效应要受到附近其他山体的影响。Cao[13]在风洞中研究了来流方向地面和山体表面粗糙度对山体被风面流动分离特性的影响。Lubitz[14]通过风洞试验研究了来流风向角对二维和椭圆形底面三维山体不同位置处加速比的影响,并与实地风速资料进行了对比。
然而以上大量研究和算法仅局限于山顶处的平均风速特性,而忽略了山体其他位置的风场特性和对于高层建筑风振响应有较大影响的脉动风速特性。
本文通过10个不同坡度和高度的三维轴对称山体模型风场特性试验,研究了平均风速加速效应和脉动风速均方根值与山体坡度、高度的关系,提出了山体加速效应修改模型,建立了脉动风速均方根增大值分布模型,可为山地风场中高层建筑风荷载及风振响应计算提供依据。
1 试验概况
试验在中国空气动力研究与发展中心低速所1.4 m×1.4 m风洞中进行,模型几何缩尺比为1:1000,采用聚氯乙烯泡沫制作,图1所示为某山体试验图片,图2为山体几何形状和平均风加速效应示意图。

图1 山体模型Fig.1 A hill model

图2 山体形状及加速效应示意图Fig.2 Schematic diagram of a hill and the speed-up effect
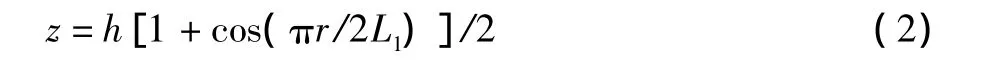
采用排管和电子扫描阀采集脉动风速信号,排管高700 mm,平均分布20根探针,扫描阀采样频率156Hz。用尖塔和粗糙元模拟了中国荷载规范中的B类地面粗糙度风场,平均风速和湍流度剖面如图3所示,平均风速剖面指数α为0.167。脉动风速谱与Davenport谱相比较为吻合,如图4所示。试验湍流积分尺度0.2 m,换算到实际尺度200 m,与大气边界层的湍流积分尺度基本一致。
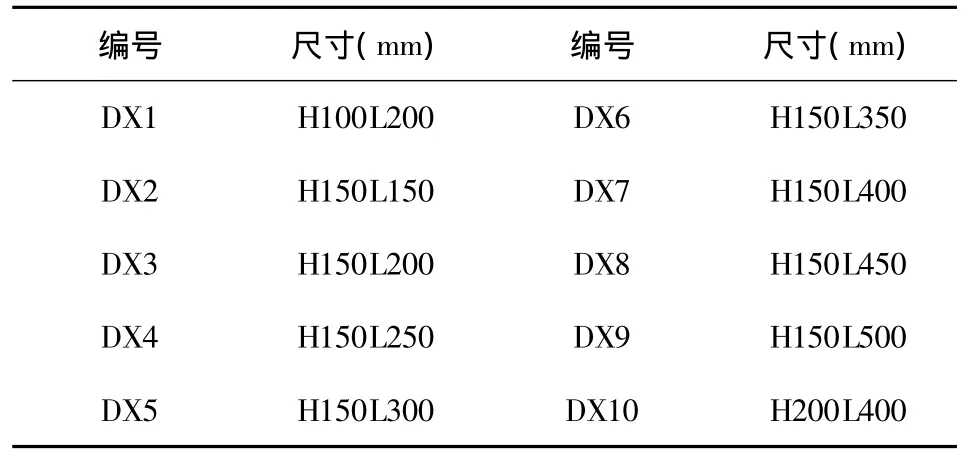
表1 山体模型尺寸Table 1 Size of hill models

图3 平均风速和湍流度剖面Fig.3 Vertical profile of mean velocity and turbulent intensity
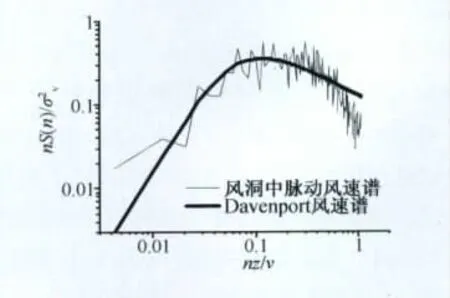
图4 脉动风速功率谱Fig.4 Power spectrum density of fluctuate wind velocity
2 山地平均风速特性及数学模型
Jackson[1-2]提出的算法中,对于山顶最大加速比的规定为:
三维轴对称山体:
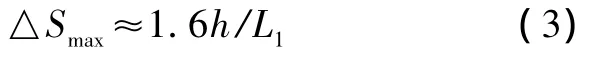
二维对称山体:

虽然式(3)和(4)仅仅考虑了山体的几何形状,而忽略了山体局部地面粗糙度、风场类型等因素的影响,但简单适用,影响深远。
Taylor[6]提出的“原始算法”,可以计算山顶不同高度处的加速比:
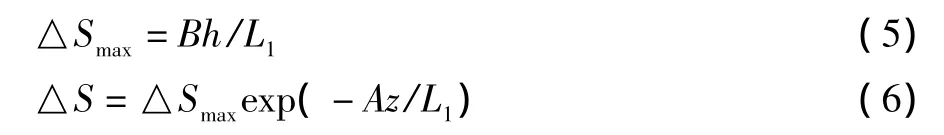
其中A和B是两个经验常数,根据山体几何条件不同而不同,但未考虑地面粗糙度等其他因素的影响,其取值如表2所示。

表2 原始算法中常数取值Table 2 Coefficients for use with original Guidelines
Weng[10]在“原始算法”的基础上,考虑了地面粗糙长度z0的影响,提出了新的加速比算法,可以根据地形、粗糙度的不同而取值不同。
以上三种算法代表了加速效应研究发展的三个时代,算法的合理性和适用性逐步改善。但由于实际情况影响因素太多,以上算法均只针对山顶的平均风速情况,且认为山顶最大加速比与坡度成线性关系,这显然是不合理的。
本节通过10个不同坡度和高度的山体模型,在原始算法的基础上,讨论平均风速各位置加速比随山体坡度和高度的变化规律。
2.1 山体各位置平均风速特性对比
每个工况采集10个不同山体位置的风剖面,分别是迎风面山脚、迎风面山腰、山顶、背风面山腰、背风面山脚,以及背风面山脚后 h、2h、3h、4h、5h处的 5个位置。
图5为坡度最大的模型DX2各位置的平均风速剖面图,其中虚线表示未受山体干扰时的平地风场风速剖面,实线表示山体风场中的风速剖面。可看出迎风面山脚的风剖面几乎与平地风场重合,可视为没有变化;迎风面山腰处风速已经开始增大,当到达山顶时平均风速的增加达到最大值,特别在临近地面处最为显著;刚进入背风面区域,由于山顶处造成的空气流动分离,导致山顶高度以下区域风速迅速减小,在背风面山脚最为明显,整个山顶高度以下区域风速几乎都为0。再往背风面方向,近地面风速则逐渐增大,到背风面山脚后5h距离处基本恢复到来流风速剖面,山体影响基本消失。
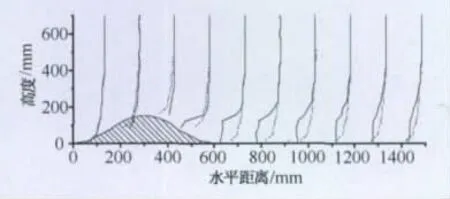
图5 山体各位置的平均风速剖面示意图Fig.5 Vertical profile of mean velocity at each location of a hill
图6为模型DX2四个典型位置的加速比对比图。在迎风面山脚,各高度加速比绝对值不超过0.1,不受山体影响;山顶近地面加速比接近0.7,随着高度的增加迅速减小;背风面山脚最底部4个高度处加速比达到-0.7左右,说明此处平均风速极小,然而在山顶高度以上,加速比基本为0,不受山体影响;在背风面山脚后5h,近地面加速比绝对值减小到0.2以下,山体对平均风速的影响基本消失。
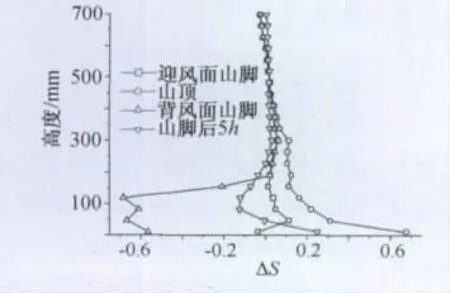
图6 模型DX2四个位置的加速比Fig.6 Speed-up ratio of 4 location of model DX2
根据山体不同位置的加速比分布规律,可认为迎风面山脚和背风面5h后各高度加速比为0,刚经过山顶进入背风面时加速比也由最大变为0;迎风面山脚到山顶、山顶到背风面山脚、背风面山脚到其后5h处的加速比随水平距离线性分布。因此对于山体坡度和高度影响的研究重点应集中在山顶和背风面山脚。
2.2 山体坡度的影响
图7所示为DX2~DX9共8个不同坡度山体的山顶处近地面不同高度的加速比对比图。在近地面高度加速效应最为明显,加速比随坡度的增加而逐渐变大,但明显不是“原始算法”所描述的线性关系。离山顶10 mm高度的最大加速比超过0.6,但在47 mm高度以上迅速减小,且加速比基本不随坡度的变化而改变。说明山体坡度只影响到山顶近地面的加速比。
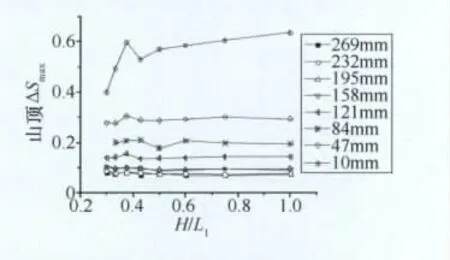
图7 坡度对山顶最大加速比的影响Fig.7 Effect of slope on maximum speed-up ratio at crest
图8为背风面山脚处近地面不同高度的加速比对比图,可见近地面平均风速均明显减小。随着坡度的增加,风速减小的幅度显著增大,最大超过了-0.8,该处平均风速已减小到接近0。在山体高度150 mm以上,减速效应消失,背风面减速效应只在山顶高度以下发生,且减速比绝对值随坡度的增大而增加。

图8 坡度对背风面山脚最大加速比的影响Fig.8 Effect of slope on maximum speed-up ratio at hill base at lee side
由图7可见,最大加速比明显不满足原始算法式(5)那样的线性关系。根据不同坡度山体风场试验,可采用以下公式对“原始算法”进行改进:

式(7)为山地近地面的最大加速比计算公式,与原始算法相比,与坡度的二次关系更符合风洞试验结果。式(8)为加速比沿高度分布规律,从图6中可看出,山顶和背风面山脚的加速比竖向分布均类似于指数分布关系,因此可用同一个公式来表示,只是参数不同,指数分布参数A由式(9)计算。根据风洞试验结果拟合得到A1、A2、A3、B1、B2五个参数。
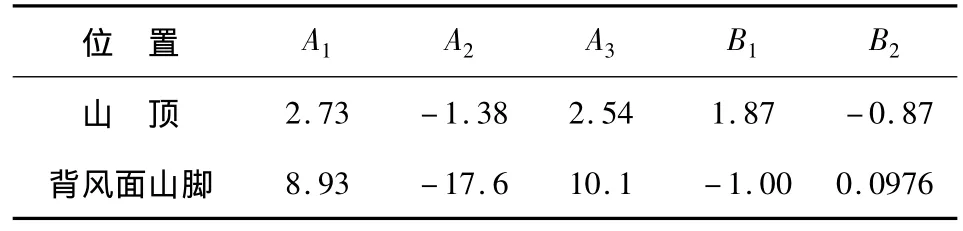
表3 加速比计算参数Table 3 Coefficients for calculating speed-up ratios
2.3 山体高度的影响
图9为坡度相等,高度不同的三个模型(DX1、DX5、DX10)山顶加速比随高度的变化情况。可看出随着山体高度的增加,近地面处的加速比显著提高,但距地面84 mm以上已经基本不受山体高度的影响。

图9 山体高度对山顶最大加速比的影响Fig.9 Effect of hill height on maximum speed-up ratio at hill base at lee side
图10为背风面山脚处加速比随山顶高度变化规律,可看出受山体高度影响的仍然只有最下部几个点。山顶高度越高,背风面山脚的影响高度越大。由于山体的绕流会出现大量流动分离或旋涡,因此背风面近地面处加速比变化显得较为杂乱;其余测点高度加速比绝对值明显随山体高度的增加而增大。
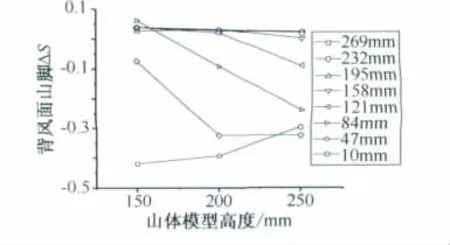
图10 山体高度对山顶最大加速比的影响Fig.10 Effect of hill height on maximum speed-up ratio at hill base at lee side
采用高度修正因子ηh来考虑平均风速加速比随山体高度的变化规律,如式(10)和式(11)所示:
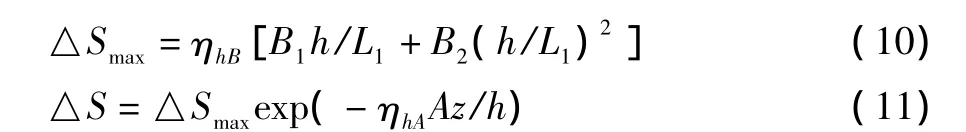
对于山顶:
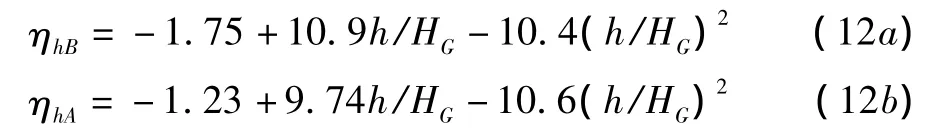
对于背风面山脚:

3 脉动风速均方根值特性及数学模型
以往绝大多数对于山地风场的研究仅局限于平均风速,忽视了脉动风速特性。
3.1 山体各位置脉动风速均方根值特性对比
图11为模型DX2各位置的脉动风速均方根值剖面图,其中虚、实现定义同图5。可见在迎风面山脚处,有无山体时的脉动风速均方根值竖向分布几乎完全重合;在迎风面山腰处的近地面,开始有细微减小;在山顶这种减小已经相当明显;一旦进入山体背风面区域,由于出现了明显的流动分离,近地面脉动风速均方根值迅速增大,在背风面山腰和山脚的近地面达到最大值;在背风面山脚之后的几个位置逐步恢复为平地分布,但每个位置在比山顶略低的高度处均会出现一个峰值,说明这个位置是山体遮挡产生的流动分离区域边线。到背风面山脚后5h距离处基本恢复到来流脉动风速均方根值剖面,山体影响消失。

图11 山体各位置脉动风速均方根值剖面示意图Fig.11 Vertical profile of root mean square of fluctuate velocity at each location of a hill
根据山体不同位置的分布规律,可认为从迎风面山脚到山顶、背风面山脚5h之后的脉动风速均方根值与平地风速相同,山顶到背风面山脚、背风面山脚到其后5h处脉动风速均方根值随水平距离线性分布。因此对于山体坡度和高度影响的研究重点集中在背风面山脚脉动风速均方根值竖向分布上。
3.2 山体坡度的影响
通过DX2到DX9共8个模型的对比,可得到山地脉动风速均方根值随山体坡度的变化规律。
定义脉动风速均方根值的增大比△Sσ:

式中:σ(z)为山地风场脉动风速均方根值,σ0(z)为平地风场脉动风速均方根值。由图11可见,迎风面山坡和山顶的脉动风速均方根值分布基本与平地情况类似,最大变化出现在背风面山脚处。
图12为不同坡度山体背风面山脚的脉动风速均方根增大比竖向分布,可见最大值均出现在120 mm左右,即0.8h处;山体的影响范围集中在200 mm以下,坡度越大,脉动风速均方根增大值越大;在200 mm以上,与平地风场基本无区别;在0.8h上下均大体呈直线分布。根据以上特点,提出以下三折线型模型:

上式中,h 为山顶高度,z为距离地面高度,△Sσmax为0.8 h处的脉动风速均方根最大增大值,zσ为山体影响高度。相同高度不同坡度的8个模型△Sσmax和zσ如图13和图14所示,可看出坡度对△Sσmax影响较大,随坡度线性增大,但对zσ的影响极小,所有坡度背风面山脚均方根增大比范围系数zσ/h都在1.6左右。

图12 坡度对背风面脉动风速均方根增大比的影响Fig.12 Effect of slope on increase of root mean square of fluctuate wind velocity at hill base at lee side

图13 △Sσmax拟合结果Fig.13 Fitting of△Sσmax
根据试验结果可以建立△Sσmax和zσ受山体坡度影响模型:
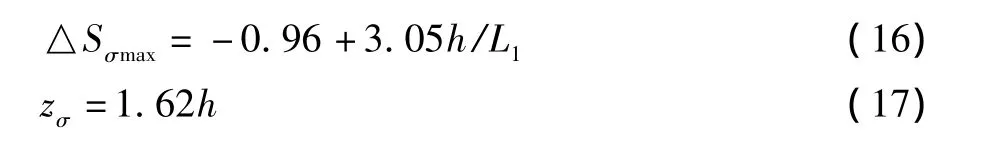

图14 zσ拟合结果Fig.14 Fitting of zσ
3.3 山体高度的影响
坡度相同,高度不同的山体脉动风速均方根值也不相同,根据模型DX1、DX5、DX10的试验结果比较,可讨论脉动风速均方根值随山体高度变化规律。
图15为三个不同高度山体模型的背风面山脚脉动风速均方根增大值竖向分布。可看出随着山体高度的增加,△Sσmax明显增大,且△Sσmax出现的高度也随之增加,基本仍出现在0.8h高度;高度越大,山体影响高度zσ也有所增加,在数值上仍保持在1.62h附近。
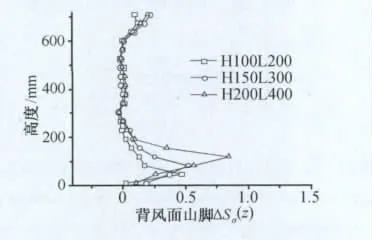
图15 高度对背风面脉动风速均方根增大值的影响Fig.15 Effect of height on increase of root mean square of fluctuate wind velocity at hill base at lee side
引入山体高度修正因子ησh考虑坡度相等,高度不同的山体引起的脉动风速均方根值差别如式(18)。采用二次多项式表示ησh随高度的变化规律,如式(19)。

4 结论
通过不同坡度和高度的10个三维轴对称山体模型风洞试验,讨论了山地平均风速和脉动风速特性随山体坡度、高度的变化规律,得到以下结论:
(1)山地平均风速在迎风面山脚与平地相同,在山顶加速最大,背风面山脚减速最大,在背风面山脚之后5h处基本恢复与平地风场相同。
(2)山顶近地面平均风速的增加量,随山体坡度和高度的增大而增大;背风面近地面平均风速的减小量和山体的影响高度,均随山体坡度和高度的增大而增大。
(3)迎风面山脚、山腰和山顶的脉动风速均方根值与平地相同,在背风面山脚处达到最大,在其之后5h处基本恢复与平地风场相同。
(4)脉动风速均方根增大值竖向分布可用三折线模型来表示,在0.8h高度得到最大值,在影响高度1.62h以上基本为0。最大均方根增大值随坡度和高度的增加而增大。
[1]JACKSON P S,HUNT J C R.Turbulent wind flow over a low hill[J].Q.J.Roy.Meteorol.Soc.,1975,101:929-955.
[2]JACKSON P S.The influence of local terrain features on the site selection for wind energy generating systems[R].Boundary Layer Wind Tunnel Laboratory Internal Report,U-niversity of Western Ontario,BLWT-1-1979,1979.
[3]HUNT J C R,LEIBOVICH S,RICHARDS K J.Turbulent shear flow over low hills[J].Q.J.Roy.Meteorol.Soc.,1988,114:1435-1470.
[4]MASON P,SYKES R.Flow over an isolated hill of moderate slope[J].Q.J.Roy.Meteorol.Soc.,1979,105:383-395.
[5]KAIMAL J,FINNIGAN J.Atmospheric boundary layer flowstheir structure and measurement[M].Oxford:Oxford University Press,1994.
[6]TAYLOR P A,LEE R J.Simple guidelines for estimating wind speed variations due to small scale topographic features[J].Climatol.Bull,1984,18(2):3-22.
[7]GONG W,IBBETSON A.A wind tunnel study of turbulent flow over model hills[J].Boundary-Layer Meteorol,1989,49:113-148.
[8]MILLER C A,DAVENPORT A G.Guidelines for the calcu-lation of wind speed-ups in complex terrain[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,74-76:189-197.
[9]TAYLOR P A.Turbulent boundary-layer flow over low and moderate slope hills[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,74-76:25-47.
[10]WENG W,TAYLOR P A,WALMSLEY J L.Guidelines for airflow over complex terrain:model developments[J].Journal of Wind Engineering and Industrial Aerodynamics,2000,86:169-186.
[11]KIM H G,LEE C M,LIM H C,KYONG N H.An experimental and numerical study on the flow over two-dimensional hills[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,66:17-33.
[12]KIM H G,PATEL V C,LEE C M.Numerical simulation of wind flow over hilly terrain[J].Journal of Wind Engineering and Industrial Aerodynamics,2000,87:45-60.
[13]CAO S,TETSURO T.Experimental study on roughness effects on turbulent boundary layer flow over a two-dimensional steep hill[J].Journal of Wind Engineering and Industrial Aerodynamics,2006,94:1-19.
[14]LUBIZ W D,BRUCE R W.Wind-tunnel and field investigation of the effect of local wind direction on speed-up over hills[J].Journal of Wind Engineering and Industrial Aerodynamics,2007,95:639-661.

