论哥德尔语句的维特根斯坦疑难——未提及自身的算术命题何以谈论自身?

张铁声

(1．青岛滨海学院，山东青岛266555;2．山西省社会科学院，太原030006)

论哥德尔语句的维特根斯坦疑难
——未提及自身的算术命题何以谈论自身?

张铁声1，2

(1．青岛滨海学院，山东青岛266555;2．山西省社会科学院，太原030006)

维特根斯坦就哥德尔语句G提出了如下疑难，这个并未提及自身的算术命题何以竟会谈论自身?借助特定元数学关系的计算机可判定性及其特征函数的算术可定义性进行深入分析，即可得出以下结论:G非但没有提及自身，甚至也没有谈论自身，而只不过是涉及了自身——是G的推论在谈论G。

哥德尔语句;维特根斯坦;提及自身;谈论自身;涉及自身

03－0012－07

一、问题的提出

哥德尔(不完全性定理的)证明的关键之点在于构造那个著名的不可判定语句。哥德尔表明，在形式算术系统P中有一个语句G，它居然断言“我在P中不可证”。G正是那个在P中不可判定的哥德尔语句，亦即G与﹁G在P中均不可证。简单地说，若假定G在P中可证，G便是真的，由其所言便有G在P中不可证，这就导致了矛盾，故有G在P中不可证;另一方面，由于G在P中不可证，由其所言便有﹁G是假的，故而﹁G在S中也不可证。

然而，维特根斯坦却就哥德尔语句G提出了一个疑难，这个疑难可表述为:这个并未提及自身的算术命题何以竟会谈论自身?他就此写道:

“21．不要忘记，这个说其自身不可证的命题，必须被认为是一个数.学.断言，——因为这并非理.所.当.然.。一个断言如此这般的结构不能被构造出来的命题必须被认为是数学命题，这并非理所当然。

这就是说，当我们说‘它谈论其自身’，就必须以一种特殊方式去理解这句话。因为在这里，由于表达式‘这个命题谈论……’的富于变化的用法，容易造成混乱。

在这个意义上，命题‘625=25×25’也在谈论它自身:也就是说，左边的数字由右边的数字相乘得出。哥德尔的谈论其自身的命题，并未提及其自身。”①这段引文的英文文本参见Blackwell Publishers出版的电子版The Collected Works of Ludwig Wittgenstein(pp385－386):21．Do not forget that the proposition asserting of itself that it is unprovable is to be conceived as a mathematical assertion－for that is not a matter of course．It is not a matter of course that the proposition that such－and－such a structure cannot be constructed is to be conceived as a mathematical proposition．That is to say:when we said:“it asserts of itself”－this has to be understood in a special way．For here it is easy for confusion to occur through the variegated use of the expression“this proposition asserts something of…”In this sense the proposition‘625=25(25’also asserts something about itself:namely that the left－hand number is got by the multiplication of the numbers on the right．Gödel’s proposition，which asserts something about itself，does not mention itself．《维特根斯坦全集》中文版(涂纪亮主编，河北教育出版社2003年版)第7卷——《论数学的基础》中的译文(见第298页)为:21．不要忘记:一个说它自身不可证明的命题，被理解为数学陈述，——因为它并非不言而喻的。一个关于某种结构不能被构造出来的命题被理解为数学命题，这不是不言而喻的。这就是说，如果有人说“他谈论自己”，那就要以一种特殊方式去理解这句话。在这里，由于混淆使用“这个命题谈论它自身……”这个表达式，因此容易造成混乱。在这种意义上，“625=25×25”这个命题也是谈论它自身;这就是说．如果人们把右边的数字相乘，就会得出左边的数字。哥德尔的那个谈论它自身的命题，没有涉及它自身。

维特根斯坦就哥德尔语句提出这样的疑难是不足为怪的，事实上，就连哥德尔本人也曾对此深感惊讶。“1930年9月哥德尔出席一个在柯尼斯堡召开的会议(《认识》第2卷内有所报道)，宣布了他的结果。卡尔纳普、海丁、冯诺伊曼与会。冯诺伊曼十分热情地对待哥德尔的结果，私下里同哥德尔讨论过一次。在这次讨论中，冯诺伊曼问:鉴于组合论对象总能映射到整数上，是否也能造出不可判定的数论命题呢?冯诺伊曼表示他相信能做到。哥德尔回答说:‘这样当然能造出一些谈到整数的不可判定命题，但其中会出现与加、乘之类的数论概念迥然不同的概念吧。’会后不久，哥德尔自己也不胜惊讶，他居然成功地将不可判定命题换成一个前方有(自然数上的)量词的多项式了。”王浩指出，正是由于“关系B(x，y，z)看样子与加、乘之类的算术运算隔得非常远”，哥德尔才对自己竟会“成功地表明这是个‘算术’谓词，即可以用加、乘借助于量词来表达的谓词”大感惊讶［1］。

如此看来，哥德尔语句的维特根斯坦疑难的确颇为费解，值得深入探讨。

二、计算机可计算性与算术可定义性

欲回答维特根斯坦疑难，也许首先应当弄清楚的就是，与表面看上去相反，形式算术系统中的公式具有出乎意外的极其丰富的“表现力”，以至于可用以定义所有的计算机可计算函数。换言之，每一个计算机可计算函数都是算术可定义的。

对于任一(定义域和值域均为自然数亦即非负整数的)函数y=f(x1，x2，…，xn)，若形式算术系统内有一含n+1个自由变元的公式F(x1，x2，…，xn，y)满足:若自变量x1，x2，…，xn分别取值a1，a2，…，an时y=f(x1，x2，…，xn)之函数值为b，则F (¯a1，¯a2，…，¯an，y)(形式算术系统内部用0，0'，0″，0‴…(或其他符号串)表示自然数0，1，2，3…，¯ai为ai的内部表示)当且仅当y=¯b(在标准解释下)为真;若x1，x2，…，xn分别取值a1，a2，…，an时y= f(x1，x2，…，xn)无定义，则F(¯a1，¯a2，…，¯an，y)无论y取何值(在标准解释下)均不为真，就称函数y= f(x1，x2，…，xn)是算术可定义的(简称为“算术的”)。令人惊异的倒不是形式算术系统的公式可以用来定义函数，而是其公式的“表现力”居然“强大”到可以定义一切递归函数。业已证明，所有递归函数都是算术可定义的。

以下我们将简略证明，(理想的或者说存储容量不受限制的)计算机可计算性与算盘机(abacus machine)可计算性等价。由于算盘机可计算性与递归可计算性等价，于是便有，一切计算机可计算函数都是算术可定义的。

所谓计算机可计算函数，严格地说，实为计算机程序可计算函数。尽管计算机程序语言种类繁多，但很多语言，尤其是高级语言的“大多数特征只是为了更加方便使用该语言来编程而添加的，它们并没有扩展语言的基本功能”［2］，而基本要素语言(Bare Bones)则析出了为通用程序设计所必需的最小一组要素。所以，计算机(程序)可计算函数，实际上等价于基本要素语言程序可计算函数。

基本要素语言之特点为:

◆变量类型为任意长的二进制数;

◆变量名必须以一个(英文)字母打头，可后接字母、数字(0～9中的任何一个)之任意组合;

◆包括3个赋值语句和一个循环结构:

◇clear name;(name可以是任一变量名(下同)，使变量值为0)

◇incr name;(使变量值加1)

◇decr name;(若变量值≠0，使之减1;若变量值=0，维持其值不变)

◇while name not 0 do;

·

·

·

end;(若变量值≠0，执行do和end之间的语句，然后返回该循环结构;若变量值=0，就跳过该循环结构，继续向下执行其他语句)

不难证明，凡基本要素语言程序可计算的函数都是算盘机可计算的。

算盘机是一种抽象计算机，其存储容量不受限制，有任意多个寄存器可供使用，其编号为1、2、3等正整数，算盘机的程序可表为带有编号的指令表，其指令仅有两种:

◆［指令编号］将寄存器n中的数值加1，然后转向指令r

◆［指令编号］如果寄存器n中的数值≠0，则将其中的数值减1，然后转向指令r;否则(如果寄存器n中的数值=0)转向指令s

为简明计，其程序一般采用流程图表示。在流程图表示法中，上述指令可分别以图1中的初等运算流程a和b表示(其中标有e的箭头指向减1运算之后要执行的操作)［3］。

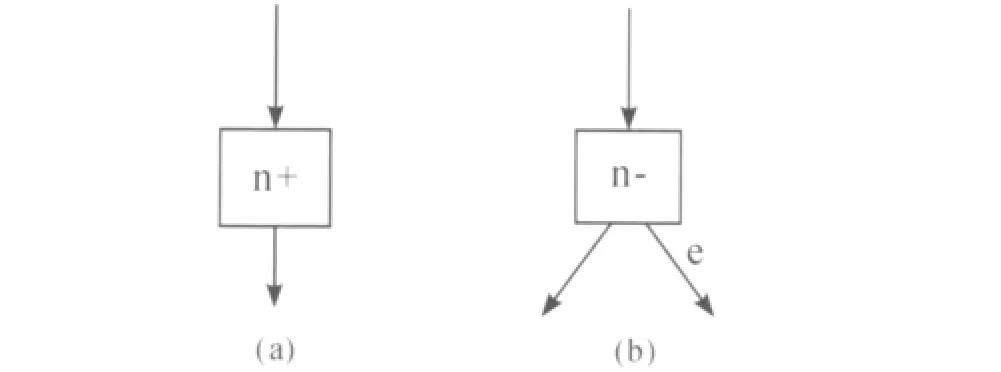
图1 算盘机流程图中的初等运算流程

显然，初等运算流程a、b分别与基本要素语言中的语句“incr name”以及“decr name”等效。进一步，运用这两种初等运算流程还可实现基本要素语言中另一赋值语句“clear name”以及循环结构的功能。不难看出，图2中的流程c和d分别与之等效。

图2 与“clear name”以及“while－end”循环结构等效的流程

由于计算机可计算函数都是基本要素语言程序可计算的，而后者实际上又均为算盘机可计算的，所以，计算机可计算函数也都是算盘机可计算的。不难看出，反之亦然。于是便有，计算机可计算性与算盘机可计算性等价。

我们知道，图灵机可计算性、算盘机可计算性、递归可计算性这三种可计算性概念是等价的［3］。由于计算机可计算性等价于算盘机可计算性，于是便有，这四种可计算性等价。业已证明，递归(可计算)函数乃是算术可定义的，于是便有，与之等价的函数类，特别是计算机可计算函数也是算术可定义的(见图3)。

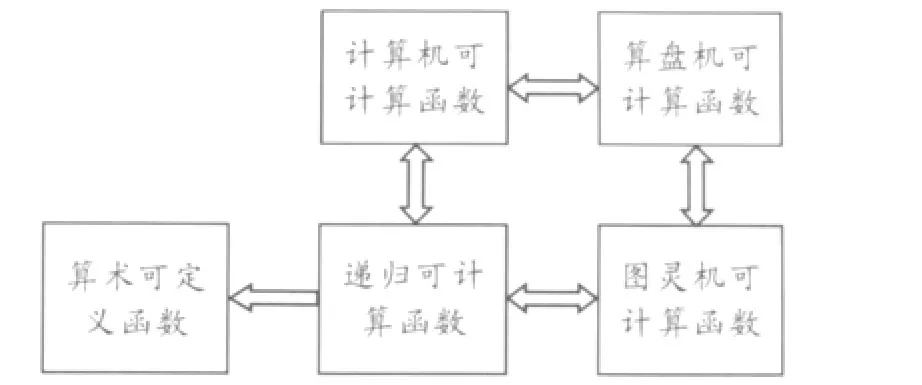
图3 四种函数类的等价性及其算术可定义性

三、元数学关系与计算机可计算性

欲回答维特根斯坦疑难，还有必要弄清楚以下事实，那就是某些元数学(关于形式算术系统的语形的或者说句法的)关系(成立与否)是计算机可判定的，换言之，其(基于哥德尔编码的)特征函数是计算机可计算的。借助上一节的结论，由此即可进一步推知，由这些关系的判定程序所确定的函数乃是算术可定义的。

哥德尔编码的方法并不限于一种，实际上只要满足以下要求即可:

(1)为形式算术系统的每个初始符号分别配以一个为其所特有的自然数(此即初始符号的哥德尔数);

(2)在此基础上，给出初始符号的有限序列(符号串)的编码规则，该规则应使其分别对应于一个为其所特有的自然数(此即初始符号的有限序列的哥德尔数)，并且任给一自然数均可依据该规则确定其是否初始符号的有限序列的编码数以及(在肯定的情况下)相应的序列为何;

(3)进而给出初始符号的有限序列之有限序列(符号串的有限序列)的编码规则，该规则应使其分别对应于一个为其所特有的自然数(此即初始符号的有限序列之有限序列的哥德尔数)，并且任给一自然数均可根据该规则确定其是否初始符号的有限序列之有限序列的编码数以及(在肯定的情况下)相应的序列为何。

形式算术系统及其哥德尔编码都不是唯一的，以下是张家龙教授针对一种形式算术系统给出的哥德尔编码法的实例［4］。不过，此后的讨论将不失一般性。

(i)初始符号的哥德尔数

将1～14依次配给以下符号:

↔→∧∨﹁∀∃=+·'0() 1234567891011121314

将大于14的素数依次配给自然数变元:

xyz …171923…

(ii)初始符号的有限序列的编码规则

依次写出初始符号的有限序列中每一初始符号的哥德尔数，由此即可得到一个自然数的有限序列k1，k2，k3，…，kn，然后以下式计算该初始符号的有限序列之哥德尔数:

此处Pi代表第i个素数(素数按升序排列)。

(iii)初始符号的有限序列之有限序列的编码规则

依上法依次求出该序列中每个初始符号的有限序列的哥德尔数，由此即可得到一个自然数的有限序列k1，k2，k3，…，kn，该初始符号的有限序列之有限序列的哥德尔数仍以下式计算:

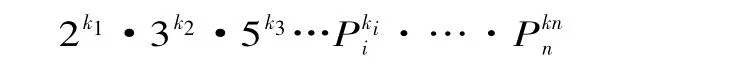
此处Pi代表第i个素数(素数按升序排列)。

在给定一种形式算术系统的哥德尔编码方法之后，我们便可使用状如“哥德尔数为m的(或者简称作“第m号”，下同)初始符号”、“哥德尔数为m的初始符号的有限序列”、“哥德尔数为m的初始符号的有限序列的有限序列”以及“哥德尔数为m的(合式)公式”、“哥德尔数为m的性质(亦即仅含一个自由变元的合式公式)”、“哥德尔数为m的语句(或命题，亦即闭公式)”、“哥德尔数为m的证明”之类的短语(摹状词)来指称特定的对象(如果这样的对象存在的话)。

上述短语形式，若将其中的m代入一个自然数，会有两种可能:一是该自然数恰为相应类型的哥德尔数，此时该短语便确有所指;二是该自然数并非相应类型的哥德尔数，此时该短语便并无所指。现在的问题是，我们有无判定此类短语是否确有所指且在回答为肯定的情况下求得其所指的算法。回答是肯定的。

对于状如“哥德尔数为m的初始符号”、“哥德尔数为m的初始符号的有限序列”以及“哥德尔数为m的初始符号的有限序列的有限序列”的短语而言，上述算法显然是存在的。以前述哥德尔编码方法为例，“哥德尔数为m的初始符号”确有所指，当且仅当m∈{1～14，大于14的素数}，其具体所指由(i)即可查得;“哥德尔数为m的初始符号的有限序列”确有所指，当且仅当将m分解为素数因子之积2k1·3k2·5k3…Pkii·…·Pknn后由相应指数构成的自然数之有限序列k1，k2，k3，…，kn恰为初始符号的哥德尔数的有限序列，并且，在回答为肯定的情况下，只要将该有限序列中初始符号的哥德尔数改写为相应的初始符号即可求得其所指;“哥德尔数为m的初始符号的有限序列的有限序列”确有所指，当且仅当，将m分解为素数因子之积2k1·3k2·5k3…Pkii·…·Pknn后得到自然数之有限序列k1，k2，k3，…，kn，再将ki(i=1，2，…，n)依上法分别分解为素数因子之积，由相应指数所得之自然数的有限序列的有限序列恰为初始符号的哥德尔数的有限序列之有限序列，并且，在回答为肯定的情况下，只要将该有限序列中的初始符号的哥德尔数改写为相应的初始符号即可求得其所指。

类似地，判定状如“哥德尔数为m的合式公式”、“哥德尔数为m的性质”、“哥德尔数为m的语句”、“哥德尔数为m的证明”的短语是否确有所指以及在回答为肯定的情况下求得其所指也均有相应的算法。

我们可先用前述算法判定m是否初始符号的有限序列的哥德尔数或者初始符号的有限序列的有限序列的哥德尔数，如果回答为否定即可做出否定的回答。如果回答是肯定的，则可进一步求得该初始符号的有限序列(或者初始符号的有限序列之有限序列)，然后依据合式公式、性质、语句或者证明之定义判定该序列究竟是否确有所指，在回答为肯定的情况下自然也可求得其所指。

附带说一下，我们甚至根本不必求出上述初始符号的有限序列(或者初始符号的有限序列之有限序列)，而只要求得相应的初始符号之哥德尔数的有限序列(或者初始符号之哥德尔数的有限序列之有限序列)作为其替身，即可判定“哥德尔数为m的合式公式(性质、语句或证明)”究竟是否确有所指。这意味着，从输入到输出，只要处理自然数便能给出判定结果(肯定时输出1，否定时输出0)。事实上，这两类算法并无本质不同，前者的结果实际上完全取决于该初始符号的有限序列(或者初始符号的有限序列之有限序列)中各初始符号的类型及其“空间”关系是否满足特定的定义，而考查相应的初始符号之哥德尔数的有限序列(或者初始符号之哥德尔数的有限序列之有限序列)中各初始符号的哥德尔数的类型及其“空间”关系是否满足相应的条件自然可以得到同样结果。

类似地，元数学关系“第m号证明是第n号公式的证明”(简记作Prf(m，n))以及“第n号证明是将第m号性质中的自由变元代入¯m后所得到的公式的证明”(简记作W(m，n))等也是计算机可判定的。换言之，其特征函数都是计算机可计算的。Prf(m，n)为真，当且仅当m确为一个证明的哥德尔数，n确为一个公式的哥德尔数，且该证明的最后一行恰为第n号公式。W(m，n)为真，当且仅当n确为一个证明的哥德尔数，m确为一个性质的哥德尔数，且该证明的最后一行恰为将第m号性质中的自由变元代入¯m后所得到的公式。W(m，n)非常重要，涉及哥德尔语句之构造，尤为值得关注。

请注意，由于上述元数学关系均为计算机可判定的，故由相应的判定程序所确定的函数乃是算术可定义的。

四、哥德尔语句:字面意义、解读与推论

关系W(m，n)的判定程序所确定的函数亦即关系W(m，n)的特征函数Fw(m，n)。既然该函数是计算机可计算的，它自然也就是算术可定义的。换言之，在形式算术系统中，存在一含有3个自由变元的公式D(x1，x2，y)可以定义该函数，亦即对任意m0、n0，若当且仅当y=时为真，若当且仅当y =时为真。亦即为真，Fw(m0，n0)=1，否则，Fw(m0，n0)=0。换言之，D为真，意味着W(m，n)的判定程序在输入为m0，n0时输出1;为假，意味着W (m，n)的判定程序在输入为m0，n0时输出0。简言之:

此即所谓哥德尔语句，为简便计，记作G。

G为真，当且仅当W(m，n)的判定程序在输入j和任意一个自然数时均输出0。

依据该判定程序之功能，于是又有:

G为真，当且仅当将哥德尔数为j的性质中的自由变元代入¯j所得之公式在形式算术系统中不可证。

由于将哥德尔数为j的性质中的自由变元代入¯j所得到的公式不是别的，恰恰是G本身，故又有:

G为真，当且仅当G在形式算术系统中不可证。

基于G的上述特点，即不难看出G与﹁G均不可证。

哥德尔语句属于仅由逻辑符号(逻辑联结词，量词，变元，等词，标点符号)以及被称为算术语言的一组非逻辑符号(如+，·，'，0)构成的“算术语句”。作为“算术语句”，G的字面意义只能是“纯算术的”:请注意，D(x1，x2， y)表示的是一个特定的含有3个自由变元的公式。尽管如此，G之所言实际上却意味着W(m，n)的判定程序(或递归算法)在输入j和任意一个自然数时均输出0。这一点之所以可能，乃是因为正如我们先前所见，计算机程序所能描述的算法本质上只不过就是加加减减及其循环(递归)计算而已，故而由此构造出来的(递归)函数恰恰适于采用“算术语句”以另一种方式来加以定义［3］，W(m，n)的判定程序所确定的函数自然也在此列，可由一含有3个自由变元的公式D(x1，x2，y)加以为真，亦即定义。由于G亦即∀的特殊构造，故有G为真当且仅当W(m，n)的判定程序在输入j和任意一个自然数时均输出0，这自然意味着将第j号性质中的自由变元代入¯j后所得到的公式在形式算术系统中不可证，又由于将第j号性质中的自由变元代入¯j后所得到的公式正是G本身，于是便可进而推知:G为真，当且仅当G在形式算术系统中不可证。不难看出，“G在形式算术系统中不可证”并非G之所言，而只不过是G的推论。

五、回答维特根斯坦疑难

现在让我们回过头来回答维特根斯坦的疑难:哥德尔语句G这个并未提及自身的算术命题何以竟会谈论自身?

在我们看来，哥德尔语句G的确是个并未(甚至也根本不可能)提及自身的算术命题，因而，严格地说，它根本不会(也根本不可能)谈论自身。所以，正确的问法也许应当是:哥德尔语句G这个并未提及自身的算术命题何以竟会涉及自身?对此则可回答如下:哥德尔语句G尽管并未提及自身却能涉及其自身之原因在于，G为真当且仅当G在形式算术系统中不可证，也就是说，G这个算术语句之真假居然与其自身在形式算术系统中可证与否相关联。G之所以具有此种奇特性质，乃是由于G为真实际上意味着元数学关系W(m，n)之判定程序在输入j和任意一个自然数时均输出0，并且反之亦然。而这又可由元数学关系W(m，n)的计算机可判定性及其特征函数的算术可定义性以及G的特定构造得到解释。

最后，再让我们逐一审视维特根斯坦的前述评语。

维特根斯坦说:“不要忘记，这个说其自身不可证的命题，必须被认为是一个数学断言，——因为这并非理所当然。一个断言如此这般的结构不能被构造出来的命题必须被认为是数学命题，这并非理所当然。”正如我们所见到的，G的确只不过是一个数学命题，甚至只不过是一个算术命题，不过，它并未“说其自身不可证”，也并未“断言如此这般的结构不能被构造出来”，所有这些只不过是G的推论。

维特根斯坦评论道:“这就是说，当我们说‘它谈论其自身’，就必须以一种特殊方式去理解这句话。因为在这里，由于表达式‘这个命题谈论……’的富于变化的用法，容易造成混乱。”显然，他的这一见解不无道理。说G“谈论其自身”，按照普通方式似乎可理解成是G的字面意义在“谈论其自身”，这显然是不确切的。在这里，只能“以一种特殊方式”将其理解成是G的推论在“谈论G”。

维特根斯坦甚至进一步发挥说:“在这个意义上，命题‘625=25×25’也在谈论它自身:也就是说，左边的数字由右边的数字相乘得出。”维氏此论颇具迷惑力。如此说来，“谈论自身”岂不成了所有的命题的“常态”?必须强调的是，如此这般的“谈论自身”与G的“谈论自身”并不是一回事。请注意“左边的数字由右边的数字相乘得出”与“625=25×25”所断言的只不过是同一个东西(亦即同样的对象具有同样的关系)而已，区别仅仅在于前者使用摹状词来指称对象并且用语词而不是用符号来表述关系。然而命题G与“谈论其自身”的命题“G在形式算术系统中不可证”所断言者却根本不是同一个东西，亦即并非在断言同样的对象具有同样的关系。

维特根斯坦指出:“哥德尔的谈论其自身的命题，并未提及其自身。”尽管意识到“谈论其自身”容易导致误解，维氏还是使用了这一表述方式。令他困惑的是:G既然并未提及其自身，又缘何能够谈论其自身?由上述讨论则可看到，G非但并未提及其自身，而且也并未“谈论其自身”，事实上，不是G而是G的推论在谈论G。

［1］王浩．哥德尔［M］．康宏逵，译．上海:上海译文出版社，2002:64，388．

［2］Brookshear J G．计算机科学概论［M］．王保江，译．北京:人民邮电出版社，2003:390－391．

［3］Boolos G S，Burgess J P，Jeffrey R C．可计算性与数理逻辑［M］．何自强，译．北京:电子工业出版社，2005．

［4］张家龙．数理逻辑发展史——从莱布尼茨到哥德尔［M］．北京:社会科学文献出版社，1993:346－347．

(责任编辑张佑法)

On Wittgenstein’s Puzzle about Gödel Sentence——Why Does the Arithmetical Sentence Which Does Not Mention Itself Assert Something about Itself?

ZHANG Tie－sheng1，2

(1．Qingdao Binhai University，Qingdao 266555，China; 2．Shanxi Academy of Social Sciences，Taiyuan 030006，China)

Wittgenstein set a puzzle about Gödel Sentence G:why does the arithmetical sentence which does not mention itself assert something about itself?The problem can be solved by deep analysis based on computer－decidability of some meta－mathematical relationships and arithmetical definability of their characteristic functions．In fact，Gödel Sentence G does not mention itself nor assert something about itself．It merely involves itself．It is the deduction to derive from G that asserts something about G．

Gödel Sentence;Wittgenstein;mentioning itself;asserting something about itself;involving itself

B81－05

A

1674－8425(2011)

2010－11－02

张铁声(1946—)，男，辽宁凌海人，青岛滨海学院教授，山西省社会科学院研究员，研究方向:思维科学、认知科学与逻辑哲学。