基于数学教育观的“理解”之理解

毕力格图，史宁中，马云鹏

（1.东北师范大学教育科学学院，吉林长春130024；2.内蒙古兴安职业技术学院数学系，内蒙古乌兰浩特137400）

基于数学教育观的“理解”之理解

毕力格图1，2，史宁中1，马云鹏1

（1.东北师范大学教育科学学院，吉林长春130024；2.内蒙古兴安职业技术学院数学系，内蒙古乌兰浩特137400）

“理解”是解释学的核心概念。基于哲学解释学的理解观，我们认为，理解本质上是以概念和关系为核心的意义复原、生成过程和存在方式，而存在方式就是认知过程与结果的相互融合。它具有主体性、相对性、差异性、循环性等基本特征。关于“理解”含义的认识与把握，对研究确定数学质量标准、数学教师专业标准以及提高数学教学质量起着关键性的作用。数学知识的系统性、严密性决定了知识之间的复杂的内在联系，要善于从整体上、本质上掌握相互关系，通过举例说明或讲故事、数学语言翻译、系统讲授、合理评价和反思等表现形式，采取梳理、综合、分类、对比、转化等方法不断提升理解者的理解水平。教师的智慧表现于教学过程，不仅要注重学习者的理解形成的过程，还要关注思考过程、探究过程中的理解。

理解；解释学；专业标准；数学认知

“理解”是教育学和心理学中普遍使用的一个词。在不同的学术范畴内，对理解有不同的解释。对“理解”这一概念含义的不同认识，导致与其相关的标准、要求与评价指标等方面问题的不同解释。就数学课程与教学而言，其主要目的之一就是促进学生对数学知识的深入、全面理解，进而不断丰富和完善学习者的认知结构，培养数学理解能力和思维能力。在数学教学实践中，人们通常把“理解”看成一种认知方式，一种获得知识的手段。而以理解为核心的哲学解释学的兴起与发展极大地丰富了教学中“理解”的内涵，也导致教育教学理念的变革。然而，数学学科之中的“理解”究竟是什么含义，人们有不同的理解与认识。正确理解与把握“理解”的含义，对研究确定数学质量标准、数学教师专业标准以及提高数学教学质量起着关键性的作用。

一、“理解”的含义

（一）辞典中对理解的不同解释

在我国，“理解”一词，最早见于元朝末年编撰的《宋史》：“心通理解”，是指从内心上明白，从道理上了解。理解，从字面上分析，“理”是指事物的缘由，“解”是指剖开、解释、解答、分析、破解或通达、推敲或推理，就是理性的思考和解读，领悟事理，依理而解。

《辞海》中将“理解”解释为“了解；领会。是通过事物间联系的揭露而认识新事物的过程。”［1］《马克思主义百科要览》（上卷）中指出“理解是辩证唯物主义认识论的一个范畴，指对事物的相互联系及其本质规律的逐渐认识过程。……所谓间接理解，是人们借用前人的经验和自身的以往经验，通过一系列的分析、综合、抽象、概括，从模糊笼统、没有分化的理解逐渐过渡到明确、清晰、分化的理解。”《马克思主义哲学大辞典》中将“理解”解释为“理性认识活动。是认识借助概念，通过分析、比较、概括以及联想、直觉等逻辑或非逻辑的思维活动。”《伦理学大辞典》中将理解解释为“一般指对人的行为、思想以及理论、观点、概念的深刻了解，懂得其含义和价值。指解释者透过生命的各种‘表现’形式（如语言、表情、艺术作品、自传等……‘理解’这一范畴有两个层次：一是对个体的理解；二是在前者的基础上对‘客观精神’（包括语言、“生活”方式、价值体系等）的理解。”《社会科学大词典》中将“理解”解释为“是逐步认识事物的联系、关系，进而明确其本质和规律的思维活动。”《黑格尔辞典》中将理解解释为“运用理性能力，以概念的形式，达到对象的真实内容的把握或理解。”

从认知层面上讲，认识得越全面，了解得越透彻，理解得就越深刻，使主体对客体有更准确的认识和把握，是了解、理解、操作、应用和推理等认知维度的核心。认知心理学认为，“理解实质上就是一个学习者以信息的传输、编码为基础，根据已有信息建构内部的心理表征、并进而获得心理意义的过程”［2］。换句话说，“理解”是主体以已有知识、经验或体验为基础，获取新的知识、经验或体验并把它融入已有认知网络系统之中，建构意义和新的认知结构的过程。理解者的理解过程是由选择、信息编码、意义重构与融合三个阶段构成。

（二）解释学关于“理解”的解释

在国外，关于“理解”的研究甚多，“理解”是当代西方一种重要的哲学学说——解释学的研究对象，即解释学的核心概念。解释学最早诞生于古希腊，是关于古典文献的注解和解释的技术，是古希腊教育的重要组成部分，主要包含修辞学和诗学两部分［3］。解释学的“理解”有两种含义：

一是“复原”说。这是一般解释学的理解观，其代表人物是施莱尔马赫和狄尔泰。理解是意义“复原”的认知过程，是主体通过语言分析和心理移情在心理上重新体验、复制和重构文本、作品的意义或作者心理背景的过程。施莱尔马赫将理解概括为“避免误解的艺术”，理解就是消除“误解”，理解的对象是人类及其生活史［4］。狄尔泰更加完善了“复原说”，并提出用移情的方法进行复原，认为理解就是从文本、作品、行为记载出发，通过语言分析和心理移情，把握作者本意、意图、情感和价值观，进而更好地构建新的认知结构，达到理解与作者原意的一致。

二是“视界融合”说。这是哲学解释学的理解观，其代表人物是海德格尔和他的学生伽达默尔。在海德格尔看来，“理解”并不是一种认知方式，它既不是主观意识的认识活动和功能，也不是获取知识的心理工具，而是所有心理活动的基础和条件，是一种存在方式［5］。伽达默尔在继承老师的基本观点的基础上提出了“理解”的“视界融合”说。他认为，理解不是一种简单意义的“复原”，而是主体“视界”和客体（文本或作品）“视界”通过观察、对话、交流，不断沟通和交融，不断生成和创造，不断丰富和拓展，进而提升为更高层次的“视界”。

纵观国内外关于理解的研究，不难发现，几乎都倾向于宏观理解，这就需要适应学科特点的微观理解即学科属性的研究，与此同时，应用性、可测性和可行性方面存在诸多问题。哲学解释学对理解内涵进行宏观与抽象辨析，而认知心理学把理解纳入到主体的心理与认知活动过程中进行研究。然而，学科教育教学改革，要以哲学和心理学理解观为理论依据，深入细致地研究学科认知规律，抓住学科内容的本质，正确把握其基本特征，清晰地认识理解的形成过程、表现形式、方法与途径，以学科核心要素为切入点进行理解。

二、“理解”的基本特征

对于理解而言，只有正确把握其基本特征，才能够结合具体的学科内容有效地指导专业实践活动。基于哲学解释学和认知心理学的理论认识，理解具有以下几种基本特征：

（一）主体性

哲学解释学宣称，“一切理解都是自我理解。理解是人的存在方式，人在理解中存在，在存在中理解。”［6］理解的目的不仅仅是为了获取对文本、作品、行为记载的原意，又是为了在已有认知的基础上理解自我、认识自我。因此，要理解必须有主体的存在，理解具有鲜明的个性化特征。

（二）相对性

主体理解与现实生活和客体相关联，都是在特定的时空的某种条件下发生。由于主体存在的状态即前理解（传统、先知、先见、成见、偏见）、语言（理解是以主体语言去理解客体语言）、间距（时空、思想、语言的间距）具有一定的历史局限性，理解都是相对的，但是相对理解也包含着绝对的成分。例如，同一个人，在初中、高中、大学学习过程中，关于函数的理解是有很大差距的。

（三）差异性

在理解过程中，由于主体所处的历史时代、传统与文化背景、思想与语言等基本条件存在着差异，主体的现实理解绝对“复原”客体原意是几乎不可能的，或者超越原意（即作者没想到的或当时根本没想过的意义），或者缺失原意（未能完全理解或根本无法想到的意义），这都是有可能的，称之为理解的差异性。要想创新和发展，缩小理解差异的范围，就需要理解主体之间进行广泛的交流和对话。

（四）循环性

从理解的发展视角分析，理解是在局部与整体、特殊与一般、文本与现实的循环中不断发生、生成和重构的过程。随着理解的基本条件的不断变化和理解者的自我反思、自我超越、自我完善，人的认知结构不断变化，进而提升理解的程度，这种循环是永无止境的动态过程，称之为理解的循环性。

三、数学理解的本质与内容特征

关于数学理解，不论是认知方式还是存在方式的观点，本质上以概念和关系为核心的意义复原、生成过程和存在方式，而存在方式就是认知过程与结果的相互融合。也就是说，数学理解对象的核心就是概念和关系，是指主体以已有的认知水平和对数学的概念与关系把握的基础上，通过某种方式或途径获取新的数学知识、思想方法、经验或体验并把它融入已有认知网络系统之中，建构意义和新的认知结构的过程。真正理解了概念和关系才能够找到最经济和简单的数学表述和论证。因此，数学学科之中的理解的内容主要由两个部分构成：

一是围绕概念的内容，即数学概念的定义、性质（概念本质的剖析）及其证明、定理（从定义和性质得出的真命题）及其证明、法则与公式及其推导过程、分类与分类标准、概念的来源与背景知识等都属于理解范畴。概念是思维的细胞，因此对概念的清晰理解是正确思维和生成意义的前提和基础。数学概念的理解包含内涵的理解（如，从定义出发准确找出概念的特征或性质）和外延的理解（如，利用确定的标准进行正确分类以及对每一个子概念的种差有清晰的认识）两个方面。就集合而言，美丽的图案、优秀学生、有用的工具、健康人、长线或短线等模糊的对象构不成集合，与集合的确定性矛盾。

二是围绕关系的内容，即已有认知结构之中的概念和新概念之间线性关系、树形关系以及简单应用、简单操作、简单推理等也都属于理解范畴，而网状关系则是应用。其中，线性关系是指头脑中的关于概念与概念、概念与故事的一对一结构；树形关系是指头脑中的关于概念与概念、概念与故事的一对多结构；网状关系是指头脑中的关于概念与概念、概念与故事的多对多结构。史宁中教授指出：数学是研究对象之间的关系，包括数量关系、图形关系、随机关系。而简单应用、简单操作、简单推理是指不超过两个步骤的应用、操作、推理。所谓步骤，假设有若干个简单命题A⇒B，B⇒C，C⇒D，D⇒E，……从A出发经过B得出C的过程称之为两个步骤。例如，从三角形的内角和为180°这一性质得出，三角形的外角和为360°、四边形可看成两个三角所以外角和为360°、五边形的……等等都是理解，但是，得出所有多边形的外角和都为360°是三角形性质的应用。

张奠宙教授指出：数学教育，自然是以“数学内容”为核心［7］。然而，数学内容的核心要素就是概念和关系，概念的形成和关系的疏通都具有层次性。教师在具体教学内容设计过程中，要关注各阶段的理解水平。依据布鲁姆分类、SOLO分类、加涅学习阶段和范希尔理论，我们认为，数学理解是具有阶段性的，是有一种合理的循环次序存在，这是由数学学科的抽象性、逻辑性、应用性等特性和理解者内在心理活动、具体的学科内容、所处的客观环境与心理环境所决定的。就以数学实例来讲，是以已有实例、正反实例、典型实例、自编实例、概括性实例等不同层次的例子为思维载体，展示抽象过程、逻辑关系、应用价值，分析特征，才能够加深理解，逐步提高认知水平。皮瑞——基伦（Pirie＆Kieren）的关于理解的理论模型［8］（见图1），非常直观地说明了理解形成过程的层次性。

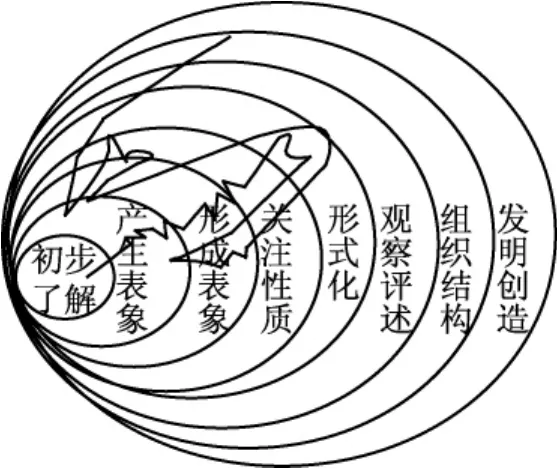
图1 皮瑞——基伦理解模型

四、有效提升数学教师理解观的建议

课程改革以来，随着教师教育理论研究和专业实践研究的深入，诸多的学科教学问题凸显出来。尤其是建立合理的教师专业标准的情况较为复杂，有必要从多视角、多维度深入细致地进行理论研究。就以数学学科而言，数学认知维度的确立是编制数学教师专业标准的关键一环。我们不但需要知道学生掌握了哪些知识技能，更需要知道学生对这些知识技能掌握到什么程度、能否利用已有的数学知识技能解决实际问题。本研究依据哲学解释学和认知心理学理论观点，将数学认知维度划分为5个子维度，即了解、理解、操作（即技能操作）、应用和推理（即演绎推理和归纳推理）。其中“理解”是核心，了解是“前理解”，操作、应用和推理是“后理解”，通过“后理解”更进一步理解、完善认知结构。前与后是相对概念，“前”是“后”的基础或条件，“后”又是“前”的深入或发展，理解正是这种循环过程中不断完善和提升。

（一）教师要全面正确把握理解的含义

作为数学教师，对“理解”的认识不能停留在日常生活中的经验水平，而应在哲学和心理学理论引领下，结合数学学科教学的基本知识、基本技能、基本思想、基本活动经验（简称“四基”）建构科学的理解观，正确把握数学理解的含义，清晰地认识理解形成过程、表现形式和方法途径，在实际教学中正确、完整、合理地表征数学知识。就以概念表征的理解为例，包括书面符号表征、图表表征、实践操作表征、语言表征、实物情境表征等等。

（二）教师要对“理解的形成过程”有清晰的认识

数学知识的系统性、严密性决定了知识之间的复杂的内在联系，要善于从整体上、本质上掌握相互关系，并通过梳理、综合、分类、对比、转化，设计形成数学理解的有效途径。教师的智慧表现于教学过程和设计与评价理念，不仅要注重学习者的理解形成的过程，还要关注思考过程、探究过程中的理解。教师只有对“理解的形成过程”有清晰的认识，才能够正确把握教学过程中的关键要素，具体与抽象、特殊与一般之间融会贯通，达到精中求简、返璞归真之效果。就以数学学科来说，理解的形成是围绕数学概念与关系，以事实、定义、实例或内涵的解析和外延的分类为载体，用归纳的方法抽象出一类事物的共同属性，逐步建构数学知识之间的认知网络的循环过程。这种网络的丰富性、复杂性和开放性决定着理解的深度与广度。由于每个个体的数学已有的“四基”存在着差异，并且受非智力因素的影响，理解形成的过程和水平有着差距。以概念为例，如下图2非常形象地展示了理解形成的一般过程［9］：

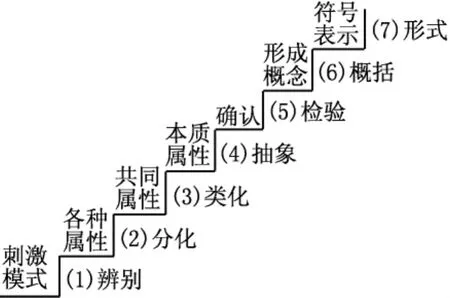
图2 概念形成的一般过程

在实际教学过程中，概念的教学有时以直接给出定义、继承已有经验或寻求发展脉络的方式进行，并融合到已有的数学知识体系之中。而理解水平体现在对事实的观察、比较、分析、综合、抽象等心智活动的广度、深度、难度和严谨性上。

（三）教师要对“理解的表现形式”有清晰的认识

以数学的理解而言，清晰地认识其表现形式是理解者形成逻辑行为程序（思考、分析、抽象、简明、演绎、推理、设计、应用、评价等）的基础，具体形式如下：

第一，能够举例说明或讲故事。史宁中教授认为：理解的重要表现之一就是能够举例说明。因为，数学思想方法、理念及潜能作为一个整体，蕴藏在一个个生动的数学案例和故事之中，它是抽象与现实的天然桥梁。举例的目的在于探究理解对象的原形或现实中的存在方式。

第二，能够灵活地翻译数学语言。数学语言是表达数学思想方法、知识和逻辑的、精心设计的专门语言，具有抽象性、准确性、简约性和形式化等特点，由符号语言、文字语言和图表语言组成，简称数学语言。数学语言之间的相互转换即翻译是理解的又一种表现形式。数学教育教学要关注引导学生自己形成思想，理解知识的关系和性质，把握数学内在的统一性，更关注理解思维和推理基础上的灵活记忆，加强数学语言的精确度、清晰度和简明性。

第三，能够系统讲解学科知识。讲解，是理解的表现形式之一，是教师运用演绎、推理、说明、分析、阐释、揭示等手段讲授学习内容的教学方法，是教师作为学生知识建构的促进者的最重要的体现形式之一。通过教师条理清晰、详略得当、措辞精当、表达流畅的讲解，使学生理解文本原意，超越或生成新的意义。讲授法有课容量大、便利理念表达、效率高等优点，系统讲解并不等于“满堂灌”，我们不要受对立世界观的影响。人们试图证明学科知识、教学知识、课程知识等知识哪一个更重要，同样对教学方法也想分出等级关系。这是徒劳的作为，分类不等于“分等级”。不管哪一种知识或方法，在教与学的过程中融为一体，相互结合或补充，交替使用才能够达到良好的教学效果。就像生物体的水分一样（如人70%以上、水母98%左右），可是我们无法直接看到，也无法评价哪一个成分更重要。

第四，能够正确评价教与学的过程与结果。哲学解释学认为，评价是一种理解方式。史宁中教授说：“知识是结果，可以是思考的结果，也可以是经验的结果，所以知识的教育是结果的教育。人的智慧表现于过程，要注重过程的教学。不仅仅是知识产生的过程，过程的教育强调学生的参与。关注学生的思考过程、探究过程，使学生能思考问题、会思考问题。”教师对课程标准、学科成分、课程实施、教学设计、师生关系等有正确的理解，才能够形成正确的评价理念，调动学生情感，提高教学质量。

第五，能够全面分析和反思教学行为。在数学学习过程之中，分析和反思是数学思维的核心，是学习者对自身的理解与行为模式的优势、劣势以及局限性所做出的理性思考，能够清晰地诊断学习过程与结果中存在的问题，分散难点，避免误解或偏见，养成良好的习惯。美国数学教育家波利亚认为：“如果没有了反思，他们就错过了解题的一次重要而有效益的方面”。

（四）教师要对“理解的方法与途径”有清晰的认识

数学教学活动，本质上是以解释、观察、交流与反思、操作、应用、评价为形式展开的理解活动。众所周知，教育教学成败的关键因素就是教师的素养。一个没有经过良好的专业实践训练的数学教师，很难摆脱狭隘和肤浅。对学生来说，教师的角色扮演能力是关键，即教师的文化心理素养（由价值取向、思维方式、审美趣味构成）和学科素养，对学生有着强大的、持久的影响力。通过名师引领、课例示范、同伴互助、专题论坛、同课异构、广泛交流等多种途径促进教师专业发展，交流理解的方法与途径，提高教师的理解能力，为学生提供丰富多彩的情景，有效激发数学学习兴趣，激励学生动脑思考、动眼观察、动手操作、动耳倾听、动身体验，也为学生提供探索与思考的余地，倡导在合作交流之中理解数学。

总之，数学教育教学要以师生发展为本，把理解的主动权交给理解者，让学习者自主探索，主动积极地建构认知结构，得到和谐地发展。新课改所提出的学习理念：“每一个学生都可以学习数学；不同的学生学习不同水平的数学；允许学生以不同的速度学习数学；学生可以用自己的方法学习数学”［10］正体现了理解性学习的观念。只有树立正确的理解观，数学教育才能够使人在自我理解、自我实现、自我创造过程中提升主体价值与意义、发展数学素养、培养数学创造性思维与能力。

［1］辞海编辑委员会.辞海［M］.香港：中华书局香港分局，1979：2312.

［2］李新成.现代认知心理学关于理解过程的研究［J］.教育理论与实践，1997（2）：45－49.

［3］金生鈜.理解与教育——走向哲学解释学的教育哲学导论［M］.北京：教育科学出版社，1997：31－39.

［4］伽达默尔.真理与方法 ［M］.上海：上海译文出版社，1999：380－385.

［5］廖青.解释学视野下的“理解”及其对教学的启示［J］.成都大学学报：教育科学版，2008（10）：8－10.

［6］王金福.解释学：对理解的理解 ［J］.赣南师范学院学报，2001（2）：6－10.

［7］张奠宙.当心“去数学化”［J］.数学教学，2005（6）：14－22.

［8］鲍健生，周超.数学学习的心理基础与过程［M］.上海：上海教育出版社，2009：131.

［9］曹才翰，蔡金法.数学教育学概论［M］.南京：江苏教育出版社，1989：67.

［10］数学课程标准研制组.数学课程标准解读［M］.北京：北京师范大学出版社，2002：2－6.

The Understanding of“Understanding”Based on the View of Mathematics Education

BI Li－getu1，2，SHI Ning－zhong1，MA Yun－peng1
（1.College of Educational Science，Northeast Normal University，Changchun 130024，China；2.Department of Mathematics，Xing An Vocational and Technical College，Hulanhaote 137400，China）

“Understanding”is the core concept of hermeneutics.Based on concept of philosophical hermeneutics of understanding theory，we think，understand is meaning recovery，the building process，and existence with concepts and relationships at the core.In addition，existence is the integration of cognitive processes and result.It has subjective，relative，difference，circulation and other basic features.Recognizing and securing the meaning of understanding plays a key role in research and enact the quality standards of mathematics，mathematics teacher professional standards and improve the quality of teaching mathematics.Systematic and rigorous of mathematical knowledge determine the complex intrinsic contact of knowledge，teacher should be good at grasping the relationship by the whole and nature idea，through the form of expression，examples or stories，mathematical language translation，systemic teaching，a reasonable evaluation and reflection，taking the methods of pectination，synthesis，classification，comparison，conversion and so on to improve the understanding levels of students.Teacher’s wisdom is reflected in the teaching process，not only focus the learner’s understanding formation process，but also concern about the understanding in the thought process and explore process.

Understanding；Hermeneutics；Professional standards；Mathematical Cognition

G42

A

1001－6201（2011）02－0159－05

［责任编辑：何宏俭］

2010－11－10

全国教育科学“十一五”规划2010年度国家重点课题（ADA100009）；教育部委托重大项目《中学教师专业标准研究》（数学、语文）

毕力格图（1966－），男，内蒙古科右中旗人，东北师范大学教育科学学院博士研究生，兴安职业技术学院数学系副教授；史宁中（1950－），江苏宜兴人，东北师范大学校长，教授，博士生导师，国务院学科评议组成员，中国教育学会副会长；马云鹏（1954－），男，吉林洮南人，东北师范大学教育科学学院教授，博士生导师，香港中文大学哲学博士。