中国经济增长均衡与非均衡的转换机制——基于Markov机制转换自回归模型的实证分析

刘力臻，张 见

（东北师范大学经济学院，吉林长春130117）

中国经济增长均衡与非均衡的转换机制
——基于Markov机制转换自回归模型的实证分析

刘力臻，张 见

（东北师范大学经济学院，吉林长春130117）

通过使用三状态三阶滞后的Markov机制转换自回归模型，笔者分析了1991年第1季度到2010年第1季度我国季度GDP增长的非线性特征，以及不同状态之间的转换机制问题。研究发现：1991年第1季度到2010年第1季度的中国季度GDP增长可以分为低增长状态、高增长状态和均衡增长状态三种情况；处于低增长状态和均衡增长状态的季度GDP增长率具有振荡收敛于其平均增长率的趋势，而处于高增长状态的季度GDP增长率具有振荡远离其平均增长率的趋势；低增长状态的平均持续期大约为46个季度，高增长状态的平均持续期为1个季度，均衡增长状态的平均持续期大约为3个季度。

经济增长；均衡；非均衡；转换机制；Markov机制转换自回归模型

一、引 言

自改革开放以来，中国经济进入了一个由市场主导的增长型的大经济周期，本文研究的是这种增长型经济周期内的中国经济增长均衡与非均衡间的转换机制。均衡和非均衡是经济增长的两种基本状态，前者反映了一个宏观经济体的经济增长的长期趋势，后者则是指其经济增长显著偏离长期趋势的状态。非均衡状态的经济增长又可以分为两种情况：增长过快和增长过慢。前者可能会导致通货膨胀，进而影响经济系统的整体均衡，严重的会形成泡沫经济及其崩溃；后者可能会导致通货紧缩，破坏经济系统的整体均衡，严重的会危及社会稳定。显然非均衡增长是一种不健康的经济增长。

Markov机制转换模型主要用于研究变量关系的突变，以及变量不同关系之间的转换机制，因此成为研究经济增长在不同状态之间相互转换的主要工具。关于我国经济增长不同状态的实证研究主要有两种观点：第一种观点认为经济增长分为扩张和收缩两种状态；第二种观点认为经济增长分为扩张、稳定和收缩三种状态。基于两种状态的代表性实证研究主要有：刘金全等（2005）结合Markov机制转换模型和Plucking模型，定量分析了我国经济周期波动性与阶段性之间的关联［1］。王建军（2007）对传统的Markov机制转换模型进行了修正，在传统的Markov机制转换模型中加入了虚拟变量。他运用修正后的模型分析了1953年到2005年的年度实际产出增长率数据，研究发现，改革前后我国经济周期的非对称机制特征比较明显，并且经济增长周期模式和经济周期变化机制存在显著差异［2］。唐晓彬（2010）利用1952年到2008年的GDP年度数据，将两机制的Markov转换模型运用到状态空间模型中，对我国经济增长的周期性表现进行了细致分析，其研究结果表明Markov机制转换模型较好地刻画了我国经济增长的非对称性特征［3］。基于三种状态的代表性实证研究主要有：刘金全等（2003）通过将经济增长速度同潜在自然率水平进行对比，把经济增长分为扩张、稳定和收缩三个阶段，并用Markov转换模型估计了三种状态之间的转换概率和阶段持续性［4］。刘金全等（2009）主要使用三机制的Markov机制转换模型，研究了1994年到2009年的中国经济增长季度数据的波动特征以及经济周期阶段性变迁的可能性，并对接下来3年我国经济增长的运行趋势变化以及经济周期所处的状态进行判断和预测，他们认为金融危机的影响虽然具有一定的持续性，但是随着时间推移，我国经济处于“低速增长阶段”的可能性逐渐减小，而处于“适度增长阶段”或“快速增长阶段”的可能性不断加大［5］。张旭华（2006）运用3状态的Markov机制转换模型研究了台湾经济增长的周期性规律，实证结果表明台湾经济当前处于中速增长阶段，再次进入衰退或调整增长的可能性均不大［6］。陈浪南等（2007）采用三机制Markov均值和方差转移的二阶自回归模型和贝叶斯Gibbs抽样非参数估计方法，分析了1979年到2004年之间中国GDP季度数据。研究认为我国经济周期的非对称性主要体现在三个机制的均值、方差和转换概率的不同［7］。

本文把经济增长分为增长过慢、增长均衡和增长过快三种状态，这与已有的使用三状态Markov机制转换模型进行的实证研究并无本质区别。然而，本文所使用的非线性时间序列的Markov机制转换模型与已有的Markov机制转换模型最大的区别在于，本文的模型不仅允许在不同的机制下均值和方差可变，而且也允许在不同机制下自回归系数可变。本文的结构安排如下：第一部分，引言；第二部分，介绍本文所使用的Markov机制转换自回归模型及其极大似然估计方法，同时介绍了数据的选取；第三部分，分析结果，主要包括外生参数的估计值和状态变量的平滑概率；第四部分，政策含义。

二、模型与数据

（一）Markov机制转换自回归模型

Hamilton（1989）首先把Markov机制转换模型成功应用于经济时间序列的非线性分析［8］。其后，从理论和实证的角度出现了大量相关研究（例如Goodwin，1993［9］；Hamilton and Susmel，1994［10］；Boldin，1996［11］；Psaradakis and Sola，1998［12］；Yao and Attali，2000［13］；Moolman，2004［14］；Cologni，2009［15］等等），这些研究进一步推动了Markov机制转换模型在时间序列分析中的应用，使得Markov机制转换模型成为当前研究非线性时间序列的主要工具之一。

由于本文的模型不仅允许在不同的机制下均值和方差可变，而且也允许在不同机制下自回归系数也可变［16］，所以本文所使用的Markov机制转换自回归模型具有如下一般形式：

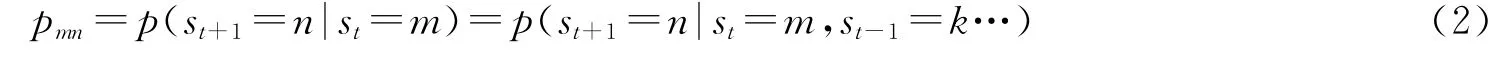
其中，pmn表示从m状态到n状态的转换概率，，可以用一个转换概率矩阵来描述状态变量st所服从的Markov过程，如下所示：

（二）Markov机制转换自回归模型的极大似然估计

极大似然估计方法是估计Markov机制转换自回归模型的一种较为经典的方法［17］。因为状态变量st∈｛1，2，…，k｝，滞后阶数为q，首先构建新的状态变量，新状态变量是由第t期到第（t－q）期的所有状态组成的有序组合：

显然，由于原状态st一共有k个状态，因此新状态变量一共有kq＋1个状态。令i＝kq＋1，则以新状态变量为基础的新的转换概率矩阵可以写成：

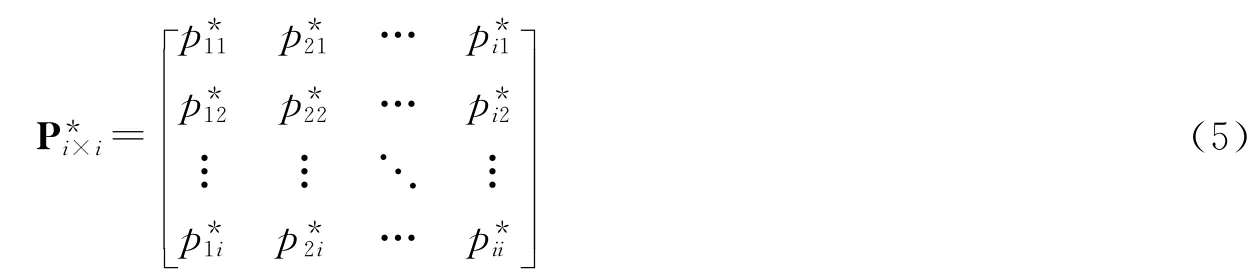
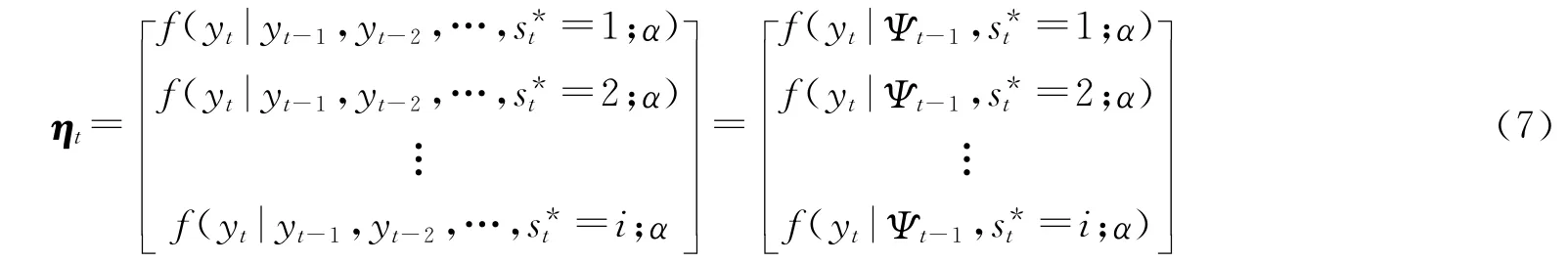
其中，Ψt－1代表（t－1）期之前的所有可观测信息集，α代表所有外生的待估计参数。显然，对于任意状态可以用可观信息集Ψt－1和待估计外生参数α来表示：

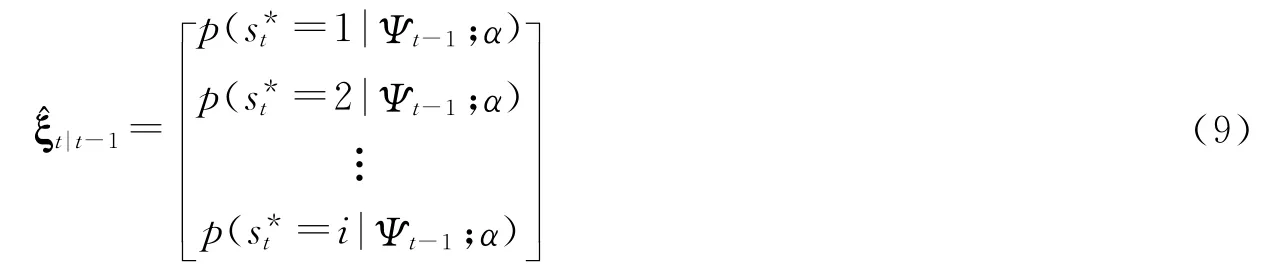
又因为：

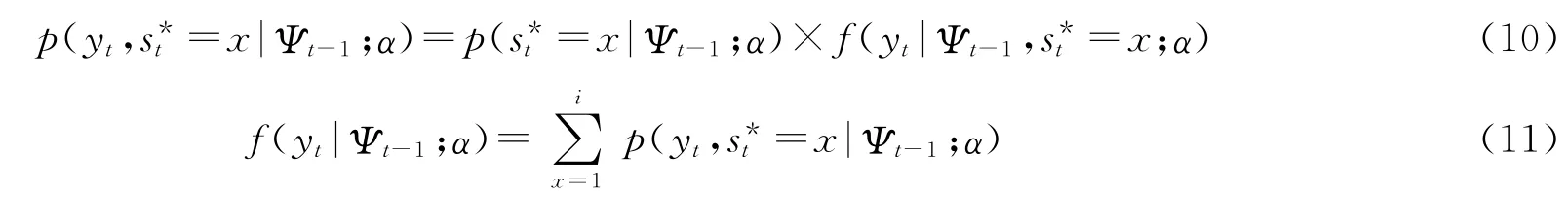
由（10）式和（11）式，可得第t期的yt在可观信息集Ψt－1和待估计外生参数α的条件下的条件概率：

第（12）式是用于构建极大似然函数的关键方程，但是很显然的是第（12）式中的f（yt｜Ψt－1；α）还不能完全用可观信息集Ψt－1和待估计外生参数α来表示，因为还不能像ηt一样显示地用可观信息集Ψt－1和待估计外生参数α来表示。

进一步，根据第（10）式和第（11）式，由Bayes定理，可得：

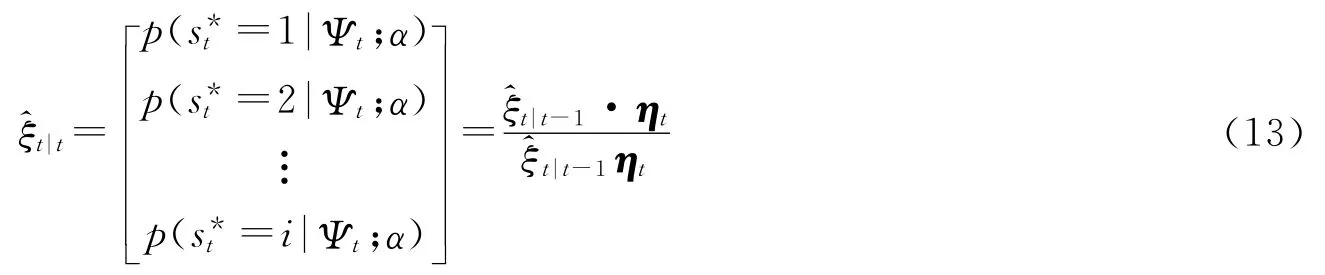
其中，·表示向量中对应元素的乘积。又因为，由第（5）式和第（9）式，可得：

综上所述，可以得到k状态q阶滞后的Markov机制转换自回归模型的对数极大似然函数：

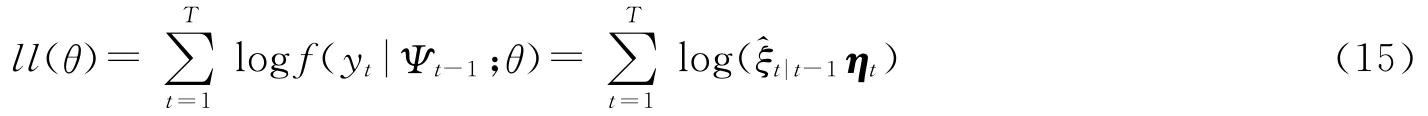
该极大似然函数由可观信息集Ψt－1、待估计外生参数α和状态转换概率矩阵P中的元素共同构成，因此，可以通过最优化第（15）来获得外生参数α和状态转换概率矩阵P的一致估计。

另外，状态变量平滑转换概率的推断通常采用Kim（1994）提出的算法［18］，计算公式如下：

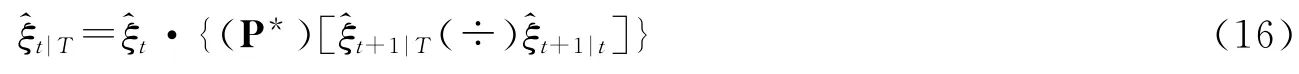
（三）数据选取

本文选取了1991年第1季度到2010年第1季度的季度GDP数据。2005年以前的数据源于《中国季度国内生产总值核算历史资料1992—2005》，其中1991年的季度GDP数据根据1992年的GDP数据及同比增长率计算得到。2005年以后的数据源于中国国家统计局官方网站。所有原始的GDP数据均被调整为1992年不变价格，并经Census X12－Additive方法进行了季节调整。在此基础上，我们计算了1991年第1季度到2010年第1季度的季度GDP的环比增长率。

如图1所示，中国经济总体上保持了一个稳定增长态势。在我们计算出来的76个季度GDP增长率中，有69个季度GDP增长率为正，总体变化相对平稳，大部分时间都保持在区间（0，0.05）之内，但是也存在局部波动相对剧烈的情况。1991年第2季度到1994年第4季度间，中国季度GDP增长率的波动相对剧烈，这正好反映了20世纪90年代初的经济过热特征以及经济调整过程。2008年第1季度到2010年第1季度的GDP增长率的波动程度也相对较大，既反映了2008年前后的全球金融危机对中国实体经济的冲击，又反映了中国经济积极应对全球金融危机的自我调整过程。

图1 1991年第1季度到2010年第1季度的GDP环比增长率

除了上述容易观察到的表面特征之外，中国经济增长率的变化是否还存在我们无法观察到的内在机制呢？如果存在，那么内在机制的具体形式又是怎样的呢？让我们用Markov机制转换自回归模型来回答这两个问题。

三、分析结果

（一）平稳性检验

平稳性是进行时间序列分析的一个重要前提，因此我们需要首先对中国季度GDP环比增长率序列进行单位根检验。Nelson、Piger和Zivot（2001）研究发现，当时间序列中存在Markov机制转换过程时，使用传统的ADF检验来判断时间序列是否存在单位根过程是非常低效力的［19］。为了更准确地判断时间序列的平稳性，我们同时使用ADF检验和Phillips－Perron检验来判断中国季度GDP环比增长率序列的平稳性。

如表1所示，综合ADF检验和Phillips－Perron检验的结果，我们可以确定中国季度GDP环比增长率序列是一个平稳的时间序列。

表1 Growth Rate of Quarterly GDP平稳性检验

（二）非线性检验

为了检验中国季度GDP环比增长率序列的非线性生成机制，需要首先构建中国季度GDP环比增长率序列的线性自回归模型。综合考虑各项指标，我们发现，滞后3阶的线性自回归模型是最恰当的。在此基础上，进一步对线性自回归模型使用Ramsey RESET检验。辅助回归方程如第（17）式所示。

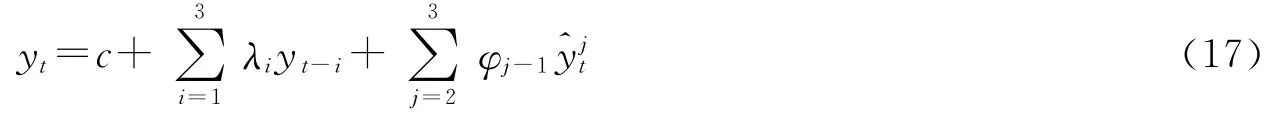
检验结果如下所示：

表2 Ramsey RESET Test

上述检验结果在1%的显著性水平上拒绝了φ1＝φ2＝0的原假设，因此，可以确定仅靠线性的时间序列模型将不能完全准确地刻画出中国季度GDP环比增长率序列的真正生成机制。

（三）参数估计

前面的分析已经指出，滞后3阶的自回归模型是最优的线性自回归模型。因此，本文所使用的Markov机制转换自回归模型是一个3状态3阶滞后的Markov机制转换自回归模型。模型参数的估计及平滑状态转换概率的计算是使用Matlab程序来实现的，本文的Matlab程序建立在Perlin（2009）的基础性工作之上［20］。参数估计的结果如下表所示：

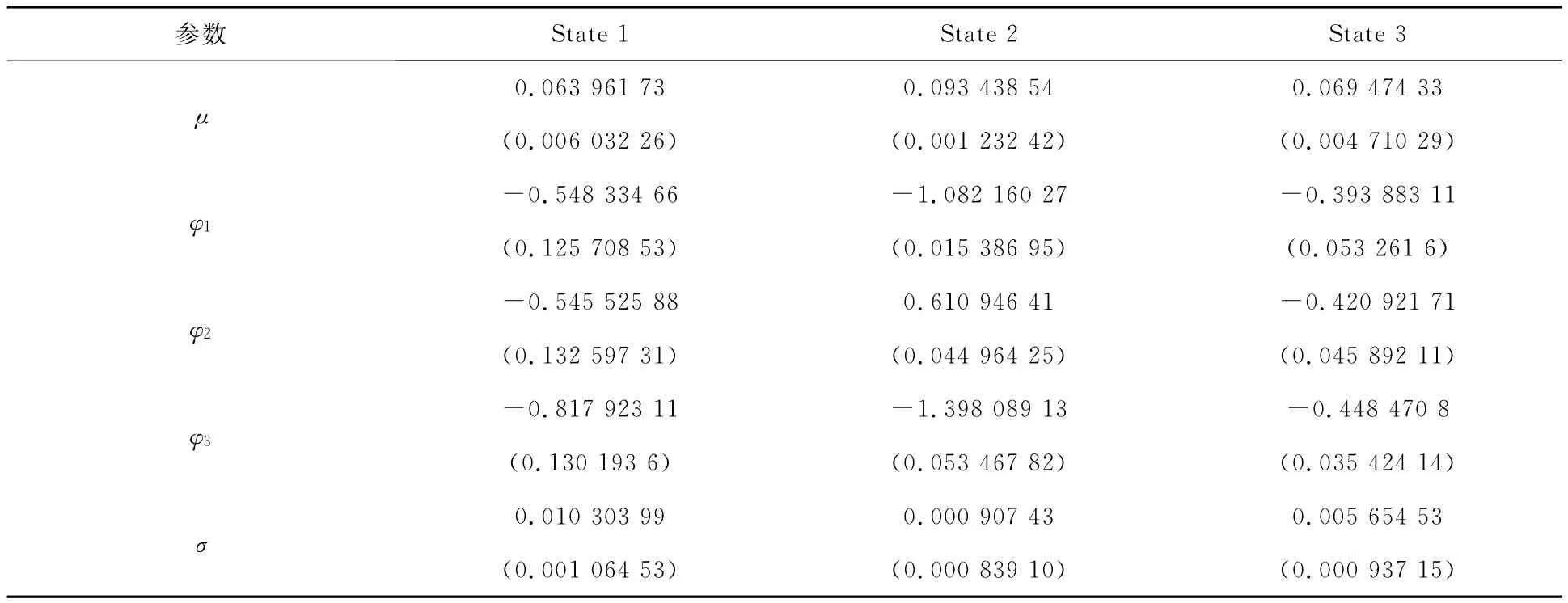
表3 参数估计结果

从表3的参数估计结果，我们有以下两点重要发现：

（2）通过对3个状态的自回归方程进行求解，我们发现：状态1和状态3将振荡收敛于其平均增长率，而状态2将振荡远离其平均增长率。具体而言，如果一个外生冲击使得时间序列偏离了状态1（或状态3）的平均增长率，表3中的状态1（或状态3）所描述的自回归机制将推动时间序列重新回到平均增长率附近。不同的是，如果一个外生冲击使得时间序列偏离了状态2的平均增长率，则表3中关于状态2的时间序列调整机制将迫使时间序列以振荡的方式无限远离平均增长率水平。这意味着经济系统一旦处于状态2，GDP增长率就会以一发不可收拾之势无限振荡扩大，但是现实经济中，这种似乎并没有出现。是什么原因导致经济系统没有出现状态2所描述的产出增长率无限振荡放大的情形呢？接下来我们将对此进行进一步的分析。

Markov机制转换自回归模型除了帮助我们找到每个状态下时间序列的自回归过程，更重要的是能帮助我们找到从一种状态到另一种状态的转换机制，这种转换可以用一个状态转换概率矩阵来描述。

表4 状态转换概率矩阵

如前所述，状态转换概率矩阵中的每一个元素都代表了从一种状态到另一种状态的转换概率，因此，从表4可知：

（1）当经济系统处于低增长状态时，其保持低增长状态的概率是0.97823362，而从低增长转换到高增长的概率几乎为0，从低增长转换到均衡增长的概率为0.02176638。这表明，经济系统一旦处于低增长状态，就将以很大的概率保持这种状态。进一步，根据公式period＝1/（1－pii），我们可以求出经济系统处于低增长状态的可能的平均持续期大约为46个季度。

（2）当经济系统处于高增长状态时，其保持高增长状态的概率接近0，而从高增长转换到低增长的概率为0.29759126，从高增长转换到均衡增长的概率为0.70240874。这表明，经济系统几乎没有保持在高增长状态的可能性，也就是说，在外生因素的影响下，经济系统一旦达到了高增长状态，这种状态的平均持续期为1个季度，然后会以0.70240874的概率转换到均衡增长状态，或以0.29759126的概率转换到低增长状态。这就解释了为什么经济系统没有出现状态2所描述的产出增长率无限振荡放大的情形。

（3）当经济系统处于均衡增长状态时，其保持均衡增长状态的概率为0.66520905，而从均衡增长转换到低增长的概率几乎为0，从均衡增长转换到高增长的概率大约为0.33479095。这表明，经济系统一旦处于均衡增长状态，就将以较大的概率保持这种状态。进一步可以求出经济系统处于均衡增长状态的可能的平均持续期大约为3个季度。

（四）平滑状态转换概率

平滑状态转换概率实际上是一种条件概率，它反映了在所有可观测信息集的条件下，所得到的每一个时期处于特定状态的概率。通过第（16）式，我们求出了中国季度GDP增长率在3种不同状态下的平滑概率曲线。

图2描述的是经济系统处于低增长状态时的平滑概率。通过观察我们发现从1995年的第3季度开始一直到2004年的第4季度这38个季度，以及2008年第1季度之后的9个季度，经济系统以接近于1的概率处于低增长状态。在我们所考察的76个样本中，经济以较大概率处于低增长的比重是61.84%。

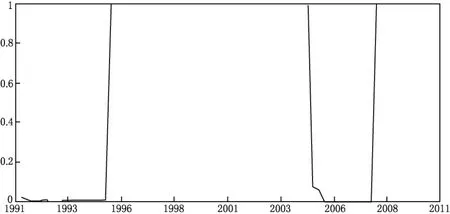
图2 经济系统处于低增长状态时的平滑概率

图3描述的是经济系统处于高增长状态时的平滑概率。如图3所示，经济系统一共有8个季度比较有可能处于高增长状态。其中，1991年第3季度以大约0.5056的平滑概率处于高增长状态，2005年第2季度以大约0.8541的平滑概率处于高增长状态，2005年第4季度以大约0.8797的概率处于高增长状态。以接近于1的概率处于高增长状态的时期有：1992年第1季度，1993年第1季度，1994年第1季度，1995年第2季度，2007年第4季度。这5个季度所处时期正好是中国经济表现过热时期，占我们所考察的总样本的比重是10.53%。

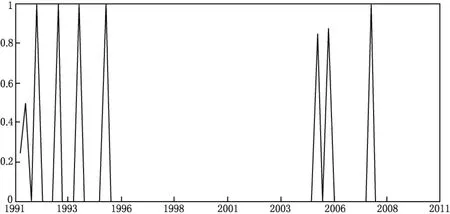
图3 经济系统处于高增长状态时的平滑概率

图4描述的是经济系统处于均衡增长状态时的平滑概率。通过观察图4，我们发现有21个季度以较大的概率处于均衡增长状态，占总样本的27.63%。具体而言，1991年第2季度的平滑概率是0.7348，2005年第1季度的平滑概率为0.9275。平滑概率接近于1的时期有：1991年第4季度，1992年第2季度到第4季度，1993年第2季度到第4季度，1994年第2季度到1995年第1季度，2005年第3季度，以及2006年第1季度到2007年第3季度。

图4 经济系统处于均衡增长状态时的平滑概率

四、政策价值

由于存在市场失灵，自发的经济增长常常会偏离均衡状态。如果仅靠市场调节，则会出现两种无法忍受的状况：一是回归均衡状态所需的时间过长；二是回归均衡状态实现方式的破坏力过大（即以经济危机、崩溃后重建的方式回归均衡状态）。要避免经济增长的非均衡状态，避免市场失灵，需要依靠宏观经济政策加以干预。

（一）政府干预经济的目标是均衡增长

经济增长状态可分为收缩、扩张和均衡三种状态，政府干预经济的目标是引导收缩和扩张的经济顺利进入均衡发展阶段。上述研究证明，当经济系统处于均衡增长状态时，其保持的概率为0.66520905，而从均衡增长转换到低增长的概率几乎为0，从均衡增长转换到高增长的概率大约为0.33479095。这表明，经济系统一旦处于均衡增长状态，就将以较大的概率保持这种状态。

（二）政府干预经济应选准介入和退出的时机

经济增长收缩、扩张、均衡的三种状态对应着三种不同的时间序列调整机制，政府干预经济的介入时机应启动于经济低增长或高增长状态的初期，从而达到既缩短非均衡增长的波动期，又使政府的干预同经济发展的客观周期相吻合，避免干预过度的双重效应，而经济增长一旦进入均衡期，政府干预就应从市场退出。

（三）政府干预经济应掌握好实施的力度

由于经济系统低增长和高增长各自接近均衡增长的概率和趋势不同，政府干预的力度应有所不同。上述研究证明，经济系统处于低增长状态是以0.02176638的概率转换到均衡增长状态，或以几乎为0的概率转换到高增长状态的，其时间序列调整机制具有振荡收敛于平均增长率的趋势，且所需时间较长，所以针对低增长状态的政府干预需要较大的力度，但需防止政府过度负债；当经济系统处于高增长状态时，其时间序列调整机制具有振荡远离平均增长率的趋势，但同时保持过高增长状态的概率接近0，说明过高增长会以剧烈动荡的崩溃方式快速终结，所以针对过高增长状态的经济，政府干预要小心谨慎，避免硬着陆。

［1］刘金全，刘志刚，于冬.我国经济周期波动性与阶段性之间关联的非对称性检验——Plucking模型对中国经济的实证研究［J］.统计研究，2005（8）：38－43.

［2］王建军.Markov机制转换模型研究——在中国宏观经济周期分析中的应用［J］.数量经济技术经济研究，2007（3）：39－48.

［3］唐晓彬.Markov机制转换的状态空间模型及其在我国经济周期中的应用研究［J］.统计研究，2010，27（2）：94－97.

［4］刘金全，王大勇.经济增长的阶段性假说和波动性溢出效应检验［J］.财经研究，2003，29（5）：3－7.

［5］刘金全，隋建利，闫超.金融危机下我国经济周期波动态势与经济政策取向［J］.中国工业经济，2009（8）：37－46.

［6］张旭华.台湾经济增长的周期和前景：一项基于Markov转换模型的实证研究［J］.亚太经济，2006（2）：64－67.

［7］陈浪南，刘宏伟.我国经济周期波动的非对称性和持续性研究［J］.经济研究，2007（4）：43－52.

［8］James D Hamilton.A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle［J］.Econometrica，1989，57（2）：357－384.

［9］Thomas H Goodwin.Business－Cycle Analysis with a Markov－Switching Model［J］.Journal of Business ＆Economic Statistics，1993，11（3）：331－339.

［10］James D Hamilton，Raul Susmel.Autoregressive Conditional Heteroskedasticity and Changes in Regime［J］.Journal of Econometrics，1994，64：307－333.

［11］Michael D Boldin.A Check on the Robustness of Hamilton’s Markov Switching Model Approach to the Economic Analysis of the Business Cycle［J］.Studies in Nonlinear Dynamics ＆Econometrics，1996，1（1）：35－46.

［12］Z Psaradakis，M Sola.Finite－Sample Properties of the Maximum Likelihood Estimator in Autoregressive Models with Markov Switching［J］.Journal of Econometrics，1998，86：369－386.

［13］J F Yao，J G Attali.On Stability of Nonlinear AR Processes with Markov Switching［J］.Advances in Applied Probability，2000，32（2）：394－407.

［14］E Moolman.A Markov Switching Regime Model of the South African Business Cycle［J］.Economic Modelling，2004，21：631－646.

［15］A Cologni，M Manera.The Asymmetric Effects of Oil Shocks on Output Growth：A Markov Switching Analysis for the G－7 Countries［J］.Economic Modelling，2009，26：1－29.

［16］Ruey S Tsay.Analysis of Financial Time Series（Second Edition）［M］.Hoboken：John Wiley ＆Sons Inc.，2005：164－167.

［17］［美］詹姆斯·D·汉密尔顿.时间序列分析［M］.刘明志译.北京：中国社会科学出版社，1999：824－849.

［18］C J Kim.Dynamic Linear Models with Markov－Switching［J］.Journal of Econometrics，1994，60（1）：1－22.

［19］C Nelson，J Piger，E Zivot.Markov Regime Switching and Unit－Root Tests［J］.Journal of Business ＆Economic Statistics，2001，19（4）：404－415.

［20］M Perlin.MS＿Regress－A Package for Markov Regime Switching Models in Matlab［CP/OL］.http：//www.mathworks.com/matlabcentral/fileexchange/authors/21596，2009.

Study on the Conversion Mechanism Between Balanced Growth and Unbalanced Growth in China's Economy：Based on the Markov Regime Switching Autoregressive Model

Liu Li－Zhen，Zhang Jian
（School of Economics，Northeast Normal University，Changchun 130117，China）

Based on the Markov Regime Switching Autoregressive Model with three regimes and three－order lags，this paper analyzes the nonlinear characteristic of the growth in China’s economy between 1st quarter of 1991and 1st quarter of 2010，and the conversion mechanism between different regimes.According to the empirical study，we find some important results：the growth in China’s economy between 1st quarter of 1991and 1st quarter of 2010can be divided into high growth，low growth and balanced growth；when the economy is in low growth or balanced growth，the growth rate shows oscillation and convergence；when the economy is in high growth，the growth rate shows oscillation and divergence；the average duration of low growth is about 46quarters，the average duration of high growth is about 1quarter，the average duration of balanced growth is about 3quarters.

Growth of Economy；Balance；Imbalance；Conversion Mechanism；Markov Regime Switching Autoregressive Model

F224.0

A

1001－6201（2011）02－0001－09

［责任编辑：秦卫波］

2010－10－12

国家社科基金重点项目（08GJA001）；东北师范大学研究生创新研究基金项目（09SSXT108）

刘力臻（1954－），女，吉林吉林市人，东北师范大学经济学院教授，博士生导师，经济学博士；张见（1981－），男，四川成都人，东北师范大学经济学院博士研究生。