指数曲线与双曲线拟合在软基沉降预测中的对比分析
周鑫,张强,曾奕衡,孙刚臣
(1.桂林理工大学土木与建筑工程学院,广西桂林 541001;2.重庆高速公路集团有限公司东南营运分公司,重庆渝北 401121;3.中铁二局第四工程有限责任公司,四川成都 610300)
指数曲线与双曲线拟合在软基沉降预测中的对比分析
周鑫1,张强2,曾奕衡3,孙刚臣1
(1.桂林理工大学土木与建筑工程学院,广西桂林 541001;2.重庆高速公路集团有限公司东南营运分公司,重庆渝北 401121;3.中铁二局第四工程有限责任公司,四川成都 610300)
简要介绍路基沉降预测方法。根据厦深客运专线福建段第2标段D1K62+780的沉降观测数据对该断面进行指数曲线和双曲线拟合,将实测数据与拟合数据对比分析,得出指数曲线在沉降预测中相对于双曲线更加准确的结论。此外,指数曲线和双曲线拟合法相对于其他的沉降预测方法都要简单,便于工程技术人员的运用。
路基沉降;沉降预测;指数曲线拟合;双曲线拟合
0 引言
随着高速铁路飞速的建设,为满足高速铁路现代化建设需要、早日实现国家大交通的设想,国家急需完善铁路路网。在建设过程中路基的不均匀沉降是导致高速铁路路基破坏众多因素之一。准确地对路基沉降进行观测和预测能够有效的控制路基工后沉降,保证路基的质量。
Lambe(1967年)[1]通过软粘土受荷作用的形变到体变的过程提出应力路基法来计算沉降。该方法对于路基沉降机理,分析常规计算中可能产生的误差趋势是很有益的,但使用较麻烦。殷宗泽等(1998年)[2]应用有限单元法考虑复杂边界条件、侧向变形、三维渗流对沉降影响、水与骨架的耦合效应对公路地基进行沉降分析最后效果良好,可是所需参数较多,有时需要三轴试验确定土体参数,过程复杂。黄少杰(2000年)[3]通过已有的沉降观测资料再根据Terzaghi的一维固结理论推算最终沉降及沉降发展过程。袁俊平等(2000年)[4]通过神经网络预测路基总沉降量,适用于只有一些沉降观测资料无土性参数情况,与实测沉降误差小,发展前景广阔。赵九斋(2000年)[5]根据现场前期实测沉降资料,用曲线拟合法预测沉降发展规律推算最终沉降量,该方法计算与以上几种方法计算相比简便,但都适用于一级线性加载情况。笔者通过厦深客运专线福建段第2标段软基沉降实测资料,用指数曲线和双曲线对沉降相对较大断面进行预测对比分析。
1 曲线预测模型[6]
1.1 曲线拟合模型
假设路基某特征点在某一观测时间的沉降量为y,当其在修筑、静载及运营过程中的变化规律应该是随时间x变化的函数。假设:
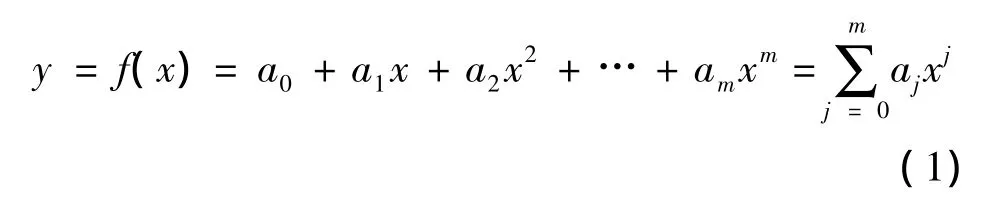
由于观测值与预测值之间存在一定的差值v1,v1也即为预测误差,则根据最小二乘法原理得:

其中,N为其特征点重复观测次数,且m<N。
由式(5)便可求出系数aj,得出预测方程y= f(x)。
假设m个最终沉降值S∞(j),对于每个S∞(j),由一组St利用最小二乘回归分析得到A(j);B(j)(i=1,2,…,m),进而可以得到对应的St的回归值以及样本平均标准偏差P(j),其中使P(j)值最小的S∞的值,亦可作为S∞的估算值。
1.2 双曲线拟合模型
沉降过程观测历时长,在沉降趋于稳定的后段取点计算,可得到较满意的结果。若在曲线前段应用便会出现较大的误差。
双曲线基本方程:
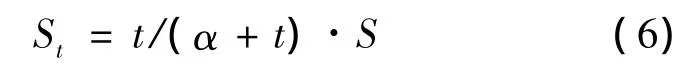
式中:α——待定系数;S——待定最终沉降量; St——在时间t时的实测沉降量(t指从施工期一半起算)。
双曲线变形方程:
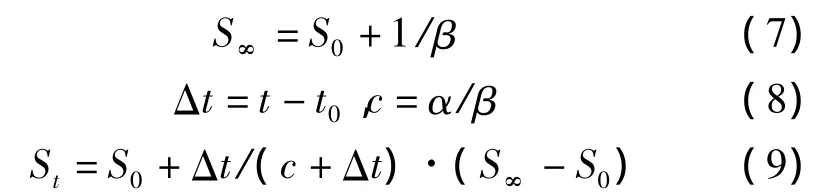
式中:α、β——地基及荷载有关的常数;Δt——时间差;S∞——路基最终沉降量;S0——路基填筑完毕时刻发生的沉降量;St——评估时路基发生的沉降量。
1.3 指数曲线拟合模型
指数曲线法又为三野法,由曾国熙1959年提出。以土层平均固结度为时间的指数函数出发,据固结度方程和固结度定义得出固结沉降表达式:
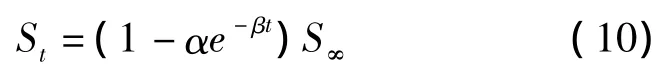
式中:St——地基t时刻的沉降量;S∞——地基最终沉降量;α、β——地基的地质条件及排水条件确定的常数。
由式(10)推导出指数曲线法表达式如下:
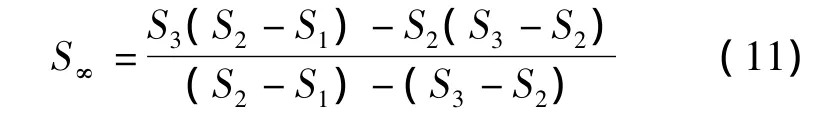
式中:S1,S2,S3所对应时间满足t2-t1=t3-t2。
指数曲线方程变形形式:St=S∞-e(At+b)或ln(S∞-St)=At+B
2 工程实例分析
2.1 工程概况
厦深客运专线福建段第2标段路堤填筑最大高度为8.3 m。基底下伏粉质粘土、淤泥质粉质粘土以及松散土、腐殖土、松软土和细砂等。其下为花岗、闪长岩全风化层或粘性土层,地震动峰值加速度为0.15g,地震动反应谱特征周期为0.40 s。地下水具弱溶出型侵蚀,酸性侵蚀pH值化学环境类别为H1。该段位于南溪河右岸,地下水水位受南溪河水位及地表降雨控制,地下水位埋深0.3~2.2 m。
软基段集中在D1K61+825.737~D1K63+ 330.061。软基基底分别采用水泥搅拌桩、振冲挤密碎石桩进行加固处理。为掌握软基断面的路基沉降特性,对于本段软基共设9个沉降观测断面。在每个断面左右路肩处布置2个沉降监测点。
2.2 曲线拟合对沉降预测分析
对厦深客运专线福建段第2标段大量观测断面数据进行分析,限于篇幅,选取沉降波动较大的D1K62+780断面进行分析,此段填土高度为6.43 m,起始填土时间为2009年7月12日,填土结束时间为2010年4月25日,观测结束时间2010年9月10日,填土观测365天,填土后观测135天,观测总天数为500天。沉降观测数据如表1~3和图1所示。
通过表2、表3的各项数据整理得到D1K62+ 780断面沉降发展趋势曲线(见图2)。
两种预测方法结果见表4。
2.3 对比分析
(1)表3和图2得出双曲线的相关系数R2= 0.9404,指数曲线的相关系数R2=0.9922,表明各级的沉降发展更接近于指数曲线的变化规律。
(2)表4可知指数曲线预测软基沉降比双曲线预测软基沉降更接近实测值,且收敛明显,相对于双曲线的预测模型能够更好的反应软基的实际沉降情况。
(3)预测前期两种曲线拟合对软基沉降预测偏差较大,预测后期各个时间的沉降与实际沉降吻合较好,预测曲线与实测曲线在恒载期内走向基本一致。
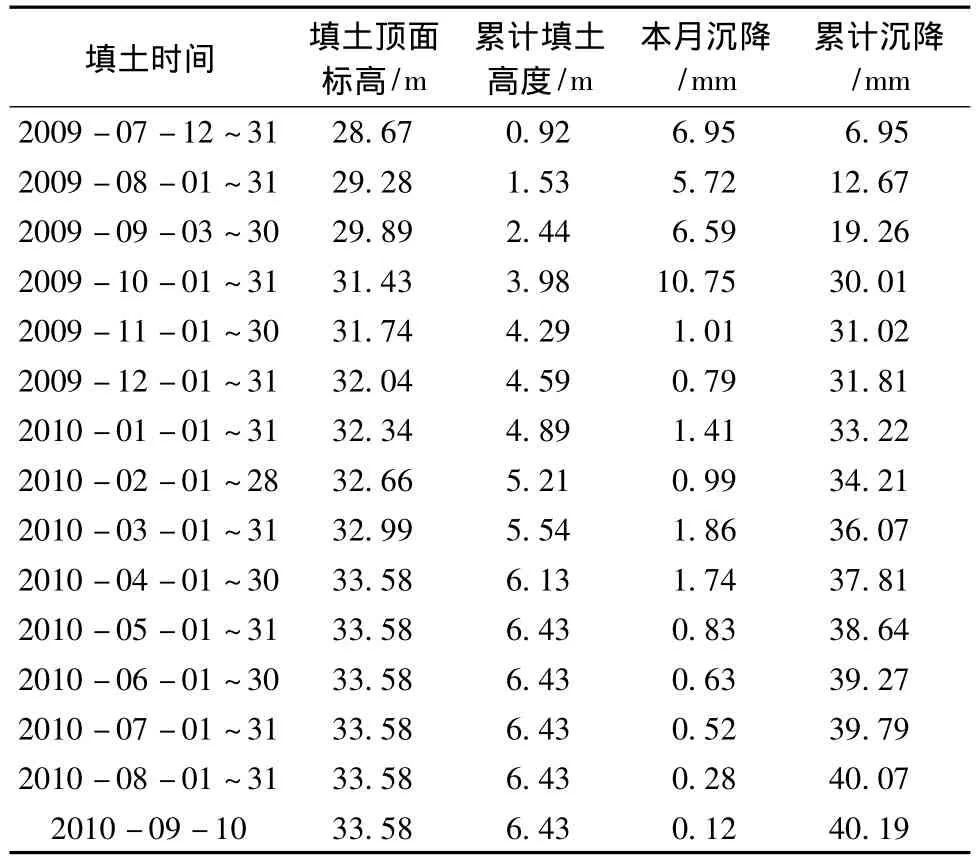
表1 D1K62+780沉降板观测数据汇总
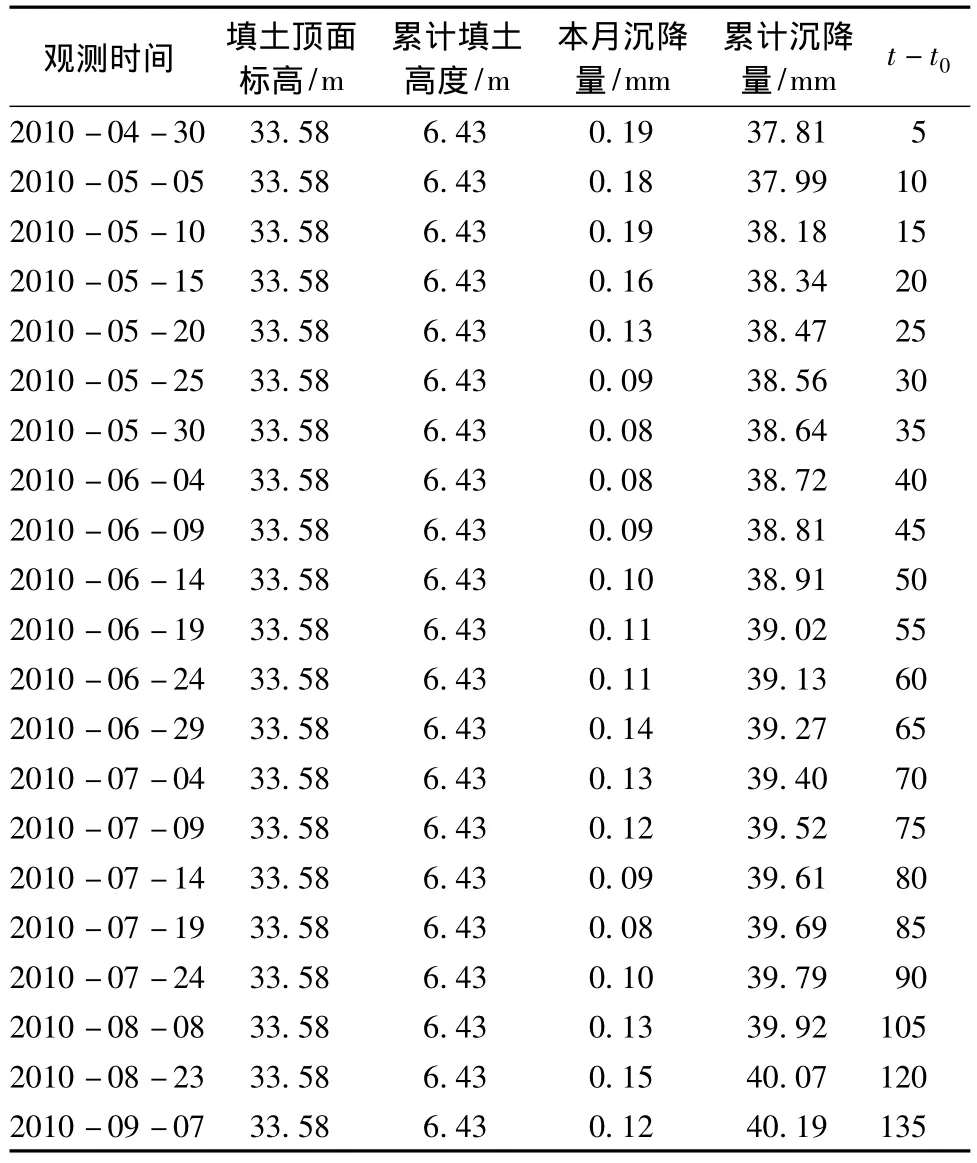
表2 D1K62+780断面等载预压期间实测沉降数据
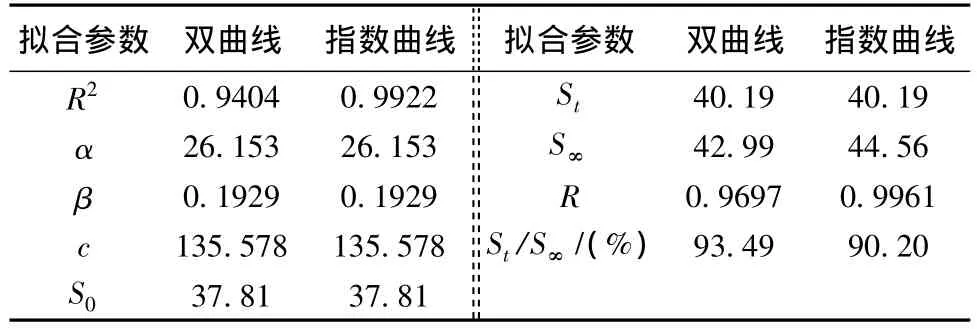
表3 D1K62+780路基沉降断面曲线拟合参数

图1 D1K62+780断面荷载-沉降-时间关系曲线

图2 D1K62+780断面沉降发展趋势曲线

表4 两种曲线预测方法的沉降分析表
3 结语
(1)通过厦深客运专线福建段第2标段软基段其中一个沉降较大的断面进行双曲线沉降预测分析和指数曲线沉降预测分析,对比了两者在同一断面沉降预测与实测沉降的准确性,得出指数曲线对软基沉降的预测相对于双曲线沉降预测更加准确。
(2)两种曲线只是在恒载期沉降才与实测沉降相吻合,对变荷载作用需考虑选用其他方法进行沉降预测。
(3)由于指数曲线和双曲线都是根据前期实测沉降资料进行后期的沉降的推算,虽然曲线拟合方法推算原理不强,理论性不够明确,预测精度不高,但是比较简明,有一定的实用性,可以根据实测数据进行初步预测,便于工程技术人员的应用。
[1]郑澄锋,等.软土路基沉降计算问题探讨[J].路基工程,2002,(4):7-9.
[2]殷宗泽,等.沪宁高速公路地基沉降有限元计算分析[J].水利水电科技进展,1998,18(2):22-26.
[3]黄少杰,等.一维反演分析预测汕汾高速公路软基沉降[J].东南大学学报,2000,30(3A):111-115.
[4]袁俊平,等.用神经网络预测路基总沉降和工后沉降[J].东南大学学报,2000,30(3A):162-166.
[5]赵九斋.连云港软土路基沉降研究[J].岩土工程学报,2000,22(6):643-649.
[6]吴大志.路基沉降计算方法及高路堤沉降稳定分析验证[D].湖南长沙:中南大学,2000.
[7]李国维,杨涛,宋江波.公路软基沉降双曲线预测法的进一步探讨[J].公路交通科技,2003,20(1):18-20.
[8]杨涛,李国维,等.基于双曲线法的分级填筑路堤沉降预测[J].岩土力学,2004,25(10):1551-1554.
[9]付宏渊.高速公路路基沉降预测及施工控制[M].北京:人民交通出版社,2007.10-22.
Contrastive Analysis on Exponential Fitting and Hyperbolic Fitting in Settlement Prediction of Soft Foundation/
ZHOU Xin1,ZHANG Qiang2,ZENG Yi-heng3,SUN Gang-chen1(1.College of Civil Engineering and Construction,Guilin University of Technology,Guilin Guangxi 541001,China;2.Chongqing Expressway Southeast Operating Company Group Co.,Ltd.,Yubei Chongqing 401121,China;3.China Railway ERJU 4thEngineering Co.,Ltd.,Chengdu Sichuan 610300,China)
Roadbed settlement prediction method is briefly introduced.According to the sedimentation data in a passenger dedicated line,exponential fitting and hyperbolic fitting were made.By the contrastive analysis on measured data and fitting data,exponential fitting was more accurate than hyperbolic fitting in settlement prediction.Being simpler than all other settlement prediction methods,exponential fitting and hyperbolic fitting are suitable for engineers and technicians.
roadbed settlement;settlement prediction;exponential fitting;hyperbolic fitting
U213.1+57
A
1672-7428(2011)11-0051-03
2011-07-29
国家自然科学基金(41062006)
周鑫(1985-),男(汉族),重庆人,桂林理工大学助理工程师、硕士研究生在读,地质工程专业,研究方向为岩土本构及地下工程,广西桂林市建干路12号,379328863@qq.com。

